4 Koordinatni referentni sistemi

Svaki prostorni podatak ima definisanu lokaciju u prostoru koja se načešće zadaje koordinatama. Koordinate u nekom koordinatnom referentnom sistemu (eng. spatial reference system (SRS) ili coordinate reference system (CRS)) su na sferi ili elipsoidu; ili u projekciji.

4.1 Geografski koordinatni referentni sistem

Geografski koordinatni referentni sistem je geometrijski model u kome je definisan:

  • Model oblika zemlje (npr: elipsoid sa parametrima a i e);
  • Početni meridijan (najčešće Grinički meridijan, što se podrazumeva i često izostavlja iz definicije);
  • Geodetski datum.

Koordinate na geografskom koordinatnom sistemu su najčešće krivolinijiske (ili elipsoidne pravougle), geodetska dužina (\((\lambda)\) longituda) i geodetska širina ((\(\mathrm{\phi}\)) latituda), i dodatno može biti zadata visina h, Slika 4.1.

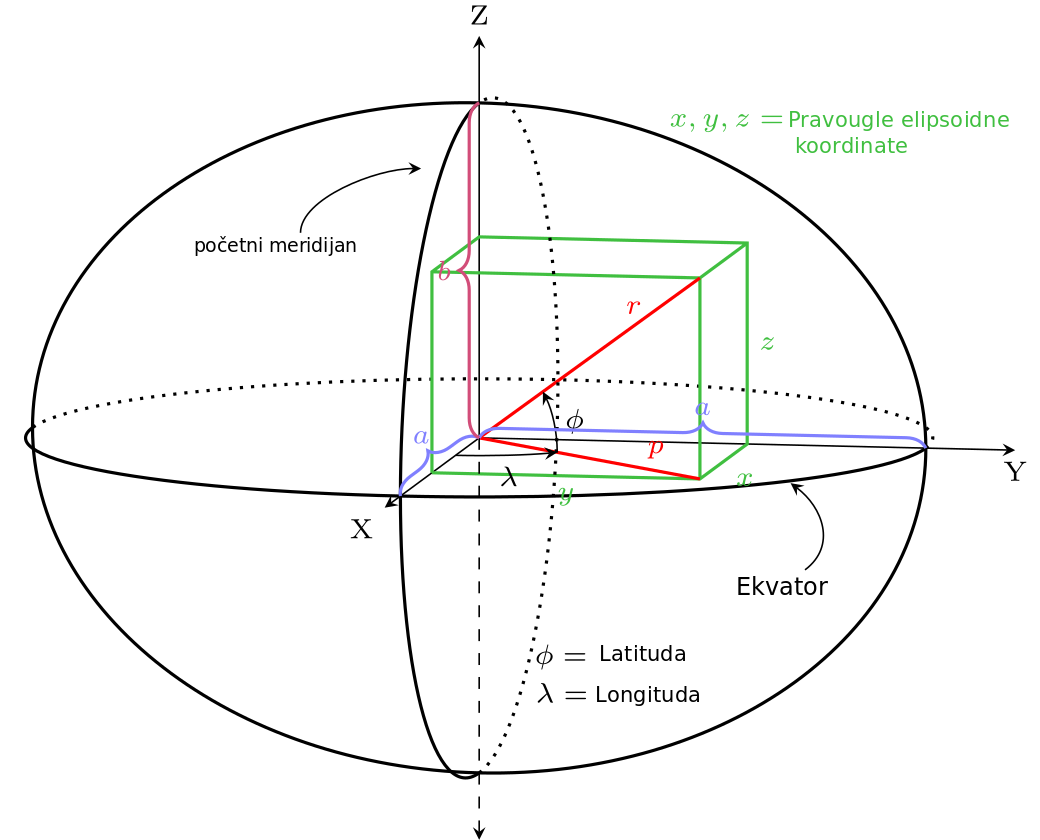
Krivolinijske koordinate za tačku geodetska dužina i geodetska širina. Koordinate su zadate na elipsoidu sa parametrima a velika poluosa i b mala poluosa. Pravougle elipsoidne koordinate su označene zelenom bojom. (Adaptirano od Krishnavedala (Own work) *CC BY-SA 3.0*)

Slika 4.1: Krivolinijske koordinate za tačku geodetska dužina i geodetska širina. Koordinate su zadate na elipsoidu sa parametrima a velika poluosa i b mala poluosa. Pravougle elipsoidne koordinate su označene zelenom bojom. (Adaptirano od Krishnavedala (Own work) CC BY-SA 3.0)

Geodetska širina je ugao između normale na ellipsoid u posmatranoj tački i ekvatorijalne ravni. Geodetska dužina je ugao između meridijana posmatrane tačke i početnog meridijana, najčešće Griniča.

Elipsoid kojim se aproksimira oblik Zemlje je dvoosni elipsoid i zadaje se sa dva linearno nezavisna parametra. Na primer, velikom i malom poluosom elipsoida (a, b), velikom osom i spljoštenošću (a, f), ili velikom osom i prvim numeričkim ekscentricitetom (a, e), neki parametri su dati u tabeli, Tabela 4.1.

Tabela 4.1: Parametri elipsoida
Parametar Opis
a Velika poluosa
f = (a-b)/a Spljoštenost
b = a- fa Mala poluosa
e2 = 2f -f 2 Prvi numerički ekscentricitet
e’ 2 = (2f - f 2)(1 - f )–2 Drugi numerički ekscentricitet

Transformacija geodetskih koordinata \(\phi\), \(\lambda\), h u pravougle geocentrične koordinate X, Y, Z može se izvesti jednačinama (Heiskanen and Moritz 1967, Aleksić, Gučević, and Popović (2009)):

\[ X=(N + h) cos\phi cos\lambda , \] \[ X=(N + h) cos\phi sin \lambda , \] \[ Z=[(1 - e^2) N + h] sin \phi . \]

gde je N radijus krivine u prvom vertikalu tačke.

\[ N = a (1 - e^2 sin^2 φ)^{–1/2} \]

Da bi se znala tačna lokacija neke tačke u prostoru, pored koordinata te tačke na elipsoidu, potrebno je poznavati i druge parametre sistema, a to su oblik elipsoida i geodetski datum. Geodetski datum je set konstanti koje definišu položaj elipsoida u odnosu na Zemlju. Datum može biti definisan na dva načina, kao topocentrični datum i geocentrični datum.

Geocentrični datum se definiše sa sedam parametara i to na sledeći način:

  • Tri parametra koja definišu položaj referentnog elipsoida u odnosu na centar Zemlje - \((\Delta X,\ \text{ΔY},\ \text{ΔZ}\)) (ili tx, ty, tz);
  • Tri parametra koja definišu orijentaciju referentnog elipsoida - \((\alpha,\ \beta,\ \gamma)\);
  • Parametar razmere - \((\mu\ (\text{ili}\ \mu=1+s))\), parametar \(s\) je najčešće u ppm (eng. parts per million – (jedan) deo na milion) jedinicama.

Slika 4.2 pokazuje odnos referentnog elipsoida (lokalnog, negeocentričnog, referenc elipsoida) i globalnog elipsoida. Globalni geocentrični elipsoid je takav da najbolje aproksimira celokupnu površ Zemlje (geoida).

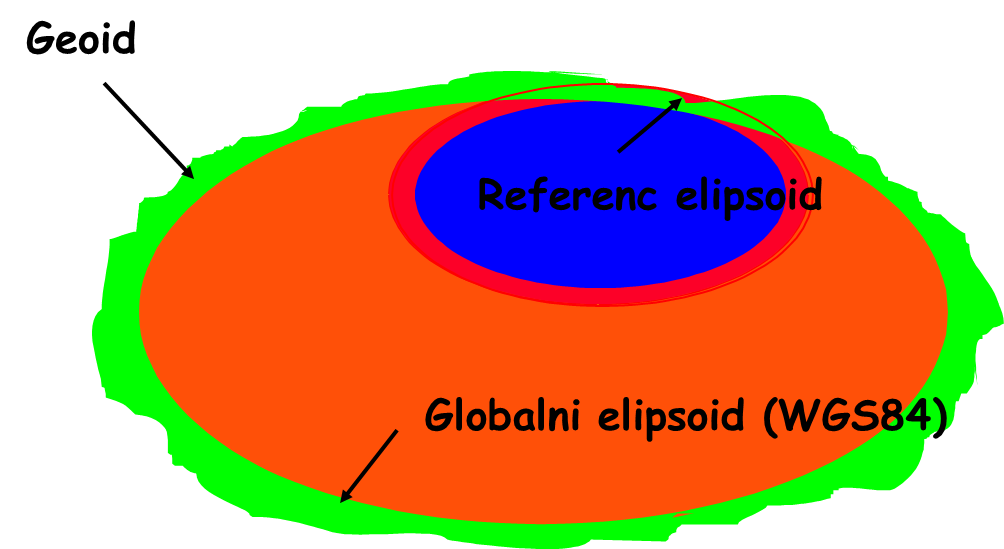
Odnos geoida, globalnog i referenc elipsoida (lokalnog elipsoida), radi ilustracije odnos je karikiran u odnosu na dimenzije.

Slika 4.2: Odnos geoida, globalnog i referenc elipsoida (lokalnog elipsoida), radi ilustracije odnos je karikiran u odnosu na dimenzije.

WGS84 je konvencionalni terestrički referentni sistem uz koji se vezuje globalni elipsoid WGS84 kojim se aproksimira geoid na celoj njegovoj površini. Centar mase elipsoida se poklapa sa centrom mase Zemlje, a ose se poklapaju sa usvojenim osama Zemlje. Prema tome sedam datumskih parametra se zadaje tako da pokazuju koliko je referenc elipsoid transliran po sve tri ose u odnosu na WGS84, koliko je rotiran po sve tri ose i koliki je odnos dužina na WGS84 i referenc elipsoidu. Referenc ili lokalni elipsoid je takav da najbolje aproksimira deo površi zemlje.

Trodimenzionalnom Helmertovom transformacijom mogu se transformisati koordinate između lokalnog elipsoida i globalnog, i obrnuto. Skup pravouglih geocentričnih Dekartovih koordinata XWGS84¸ YWGS84, ZWGS84 može se transformisati u skup negeocentričnih Dekartovih koordinata XBessel¸ YBessel, ZBessel jednačinom, u ovom primeru na Beselovom elipsoidu, koji ima datum Hermanskogel (stari Državni koordinatni sistem u Srbiji), Slika 4.3.

\[ \begin{bmatrix} X^{Besel} \\ Y^{Besel} \\ Z^{Besel} \end{bmatrix} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix} + (1 + s\times10^{-6}) \cdot \begin{bmatrix} 1&-r_z&r_y \\ r_z&1&-r_x \\ -r_y & r_x & 1 \end{bmatrix} \cdot \begin{bmatrix} X^{WGS84} \\ Y^{WGS84} \\ Z^{WGS84} \end{bmatrix}. \]

,

gde su

  • tx, ty i tz, parametri translacije po korespondentnim koordinatnim osama,
  • s parametar razmere i
  • R matrica rotacije oko koordinatnih osa XWGS84, YWGS84 i ZWGS84.

Ukoliko su uglovi rotacije \(\alpha\), \(\beta\) i \(\gamma\), oko koordinatnih osa XWGS84, YWGS84 i ZWGS84 mali (pri transformaciji rezultata iz sistema WGS84 u Državni koordinatni sistem oni su reda nekoliko lučnih sekundi), onda se matrica R može predstaviti u obliku:

\[ R=\begin{bmatrix} 1&-r_z&r_y \\ r_z&1&-r_x \\ -r_y & r_x & 1 \end{bmatrix} \approx \begin{bmatrix} 1&-\gamma&\beta \\ \gamma&1&-\alpha \\ -\beta & \alpha & 1 \end{bmatrix} . \]

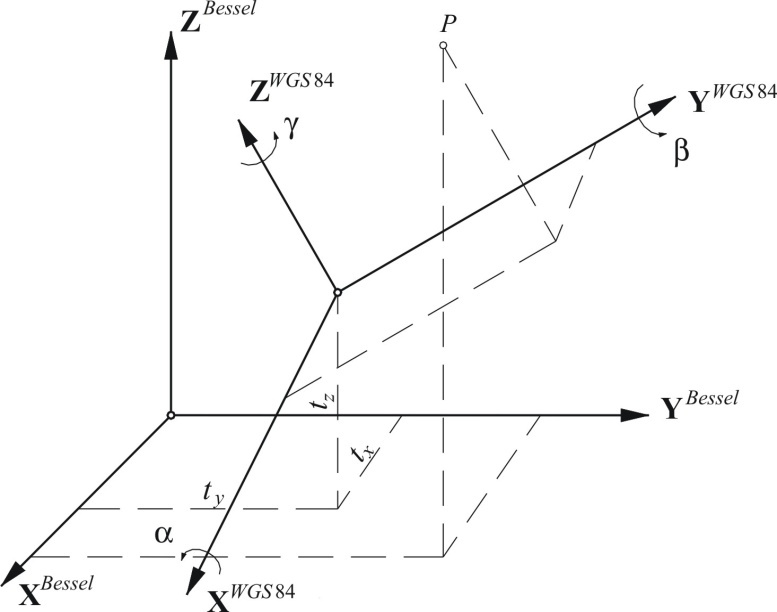
Trodimenzionalna transformacija datuma

Slika 4.3: Trodimenzionalna transformacija datuma

Prema tome, ako je poznato sedam datumskih parametara (tx, ty, tz, \(\alpha\), \(\beta\), \(\gamma\) i s), vrednosti koordinata XBessel, YBessel, ZBessel mogu se izračunati na osnovu koordinata XWGS84¸ YWGS84, ZWGS84. \[ \begin{matrix} X^{Bessel} & = & c_x+(1+s\times10^{-6})\cdot (X^{WGS84}-r_z\cdot Y^{WGS84}+r_y\cdot Z^{WGS84}),\\ Y^{Bessel} & = & c_y+(1+s\times10^{-6})\cdot (r_z\cdot X^{WGS84}+Y^{WGS84}-r_x\cdot Z^{WGS84}),\\ Z^{Bessel} & = & c_z+(1+s\times10^{-6})\cdot (-r_y\cdot X^{WGS84}+r_x\cdot Y^{WGS84}+Z^{WGS84}).\\ \end{matrix} \]

4.2 Koordinatni referentni sistem u projekciji

Najčešće su koordinate za prostorne podatke date kao pravougle koordinate u ravni karte, i uobičajeno da te koordinate imaju oznaku (x,y ili X,Y ili E,N). Formule koje se koriste da se krivolinijske koordinate sa sfere ili elipsoida (geodetske koordinate) transformišu u ravan karte predstavljaju kartografske projekcije. Tada se koordinate definišu u koordinatnom referentnom sistemu u projekciji. Kod kartografskih projekcija u procesu preslikavanja dolazi do deformacija uglova (oblika), dužina i površina. Generalno prema karakteru deformacija projekcije se dele na konformne (zadržava se jednakost oblika, uglova), ekvivalentne (nema deformacija površina) i uslovne. Računanje pravouglih koordinata iz krivolinijskih se naziva direktni kartografski zadatak, i obratno kad se računaju krivolinijske iz pravouglih naziva se inverzni kartografski zadatak.

Detaljno o projekcijama videti u literaturi (Jovanović 1984, Snyder (1987), Canters and Decleir (1989), Bugayevskiy and Snyder (2013)).

Koordinatni referentni sistem u projekciji je je geometrijski model u kome je definisana:

  • Projekcija;
  • Model oblika zemlje (npr: elipsoid sa parametrima a i e);
  • Početni meridijan (npr: Grinički meridijan);
  • Datum.

Kad su poznate koordinate u projekciji i definisan koordinatni referentni sistem, onda je moguće transformisati koordinate iz jednog koordinatnog referentnog sistema u drugi, Slika 4.4.

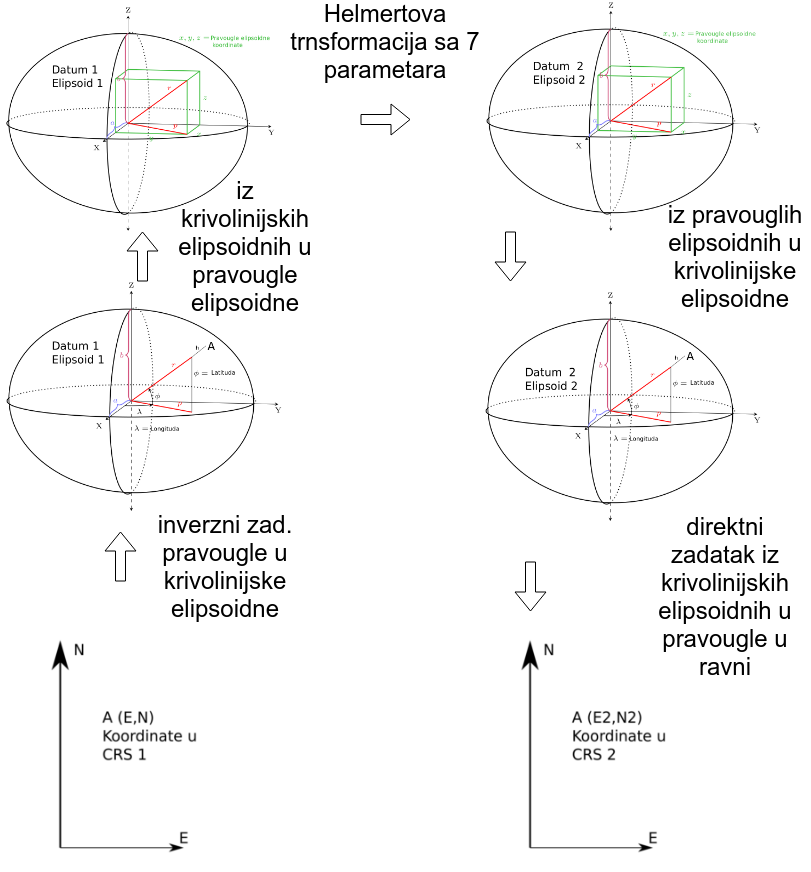
Shematski prikaz transformacije iz jednog koordinatnog sistema u projekciji u drugi.

Slika 4.4: Shematski prikaz transformacije iz jednog koordinatnog sistema u projekciji u drugi.

Literatura

Heiskanen, WA, and Helmut Moritz. 1967. “Physical Geodesy.” Bulletin Géodésique (1946-1975) 86 (1). Springer: 491–92.

Aleksić, Ivan, Jelena Gučević, and Jovan Popović. 2009. Geodetski Premer - Zbirka Rešenih Zadataka. Univerzitet u Beogradu, Građevinski fakultet.

Jovanović, Velibor. 1984. Matematička Kartografija. VGI.

Snyder, John Parr. 1987. Map Projections–A Working Manual. Vol. 1395. US Government Printing Office.

Canters, Frank, and Hugo Decleir. 1989. The World in Perspective: A Directory of World Map Projections. John Wiley & Sons.

Bugayevskiy, Lev M, and John Snyder. 2013. Map Projections: A Reference Manual. CRC Press.