8 UTM projekcija
UTM projekcija (Svetska poprečna Merkatorova projekcija ili Univerzalna poprečna Merkatorova projekcija) je izraz anglosaksonskog porekla za modifikovanu Gaus-Krigerovu projekciju. UTM projekciju su prve usvojile SAD, 1947. godine, stvarajući uslove da cela zemljina površina bude obuhvaćena jednim koordinatnim sistemom, uz ograničenje za polarne oblasti, za koje je usvojena univerzalna polarna stereografska projekcija UPS (Universal Polar Stereographic, vidi Azimutne projekcije 6, poglavlje „Stereografska projekcija“). UTM je danas standard za sve članice NATO-a i gotovo sve zemlje Evrope uključujući i Srbiju, gde je UTM projekcija usvojena za državnu projekciju, čime je Gaus-Krigerova ostala kao stara državna projekcija u kojoj i dalje ima dosta prostornih podataka, koji se u prelaznom periodu čuvaju u oba sistema.
Specifikacija projekcije:
Projekcija: Transferzalna Merkatorova (Gaus-Krigerova), sa širinom zone od \(6^o\).
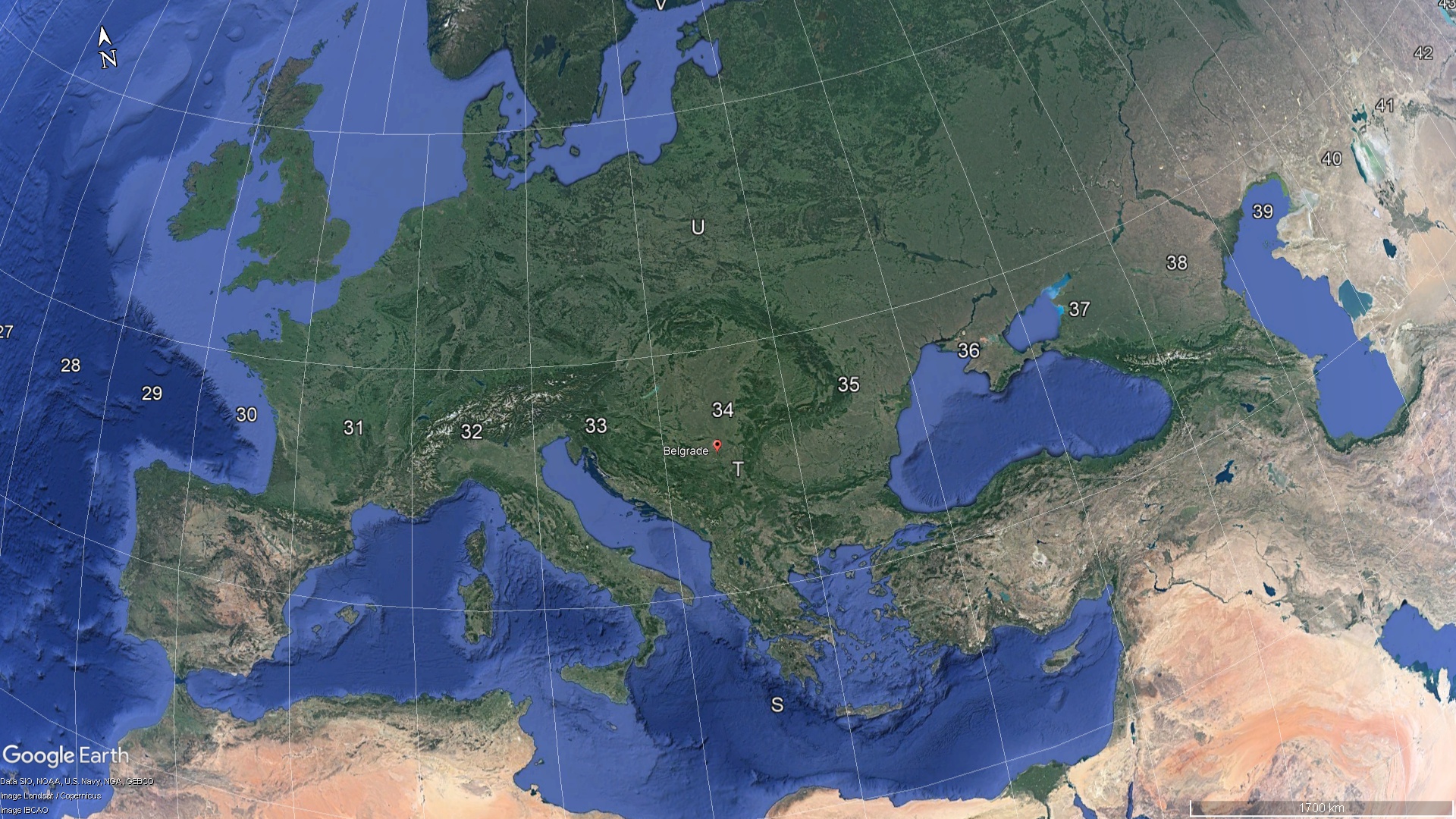
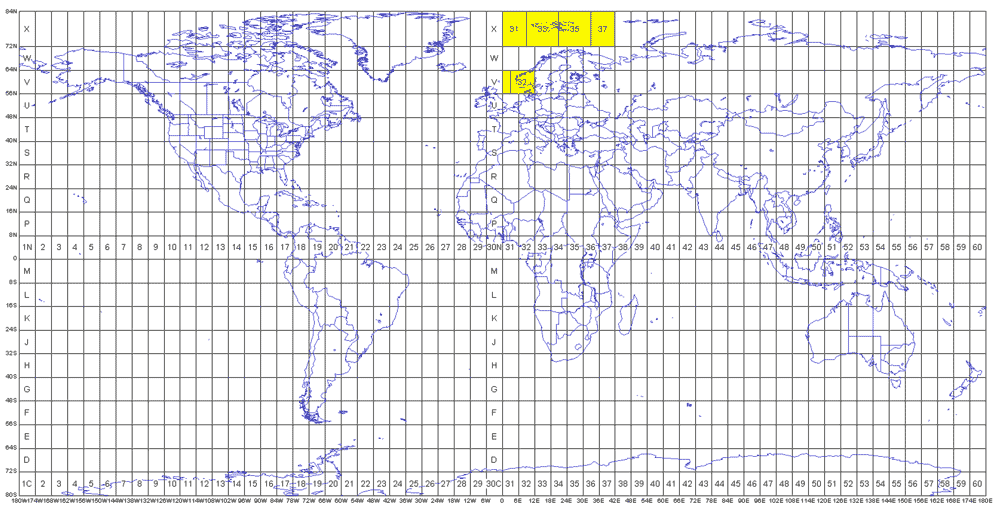
Ceo svet je podeljen u 60 zona (\(360^o/6\)), prva zona je ograničena od \(180^o\) do \(174^o\) zapadne geodetske dužine (dakle početak je suprotno od Griničkog meridijana), a šezdeseta od \(174^o\) do \(180^o\) istočne geodetske dužine, Slika 8.1.
Prostiranje projekcije po geodetskoj širini je: \(84^o\) severne geodetske širine do \(80^o\) južne geodetske širine.
Granice zona i preklop: Granični meridijani zona su oni čija je dužina deljiva sa 6 (npr. 6, 12, 18,… ,114, 120,…). Zone se preklapaju za velike razmere oko 40 km istočno i zapadno od graničnog meridijana, što izaziva negodovanje geodetskih inženjera. Ovaj preklop se nikad ne daje kada se daju reference grida.
Preklop u polarnim zonama: UTM se preklapa sa gridom Univerzalne polarne stereografske projekcije po \(30'\) u severnom i južnom području i to od širine \(83^o30'\) severno i \(79^o30'\) južno.
Na prethodnoj slici (Slika 8.1) uočljivo je da su zone podeljene na podzone. Od \(80^o\) južne geografske širine do \(72^o\) južne geografske širine je prva podzona označena sa C, sledeća zona je narednih \(8^o\) po geografskoj širini i označena je sa D, poslednja podzona je označena slovom X, od \(72^o\) do \(84^o\) severne geografske širine. Podzone su označene slovima engleskog alfabeta od C do X, s tim što se I i O ne koriste, Slika 8.2, videti i https://www.dmap.co.uk/utmworld.htm.
Napraviti funkciju koja određuje u kojoj zoni je tačka sa zadatim koordinatama:
library(sf)
lonlat2UTMzone = function(lonlat) {
utm = (floor((lonlat[1] + 180) / 6) %% 60) + 1
if(lonlat[2] > 0) {
print(paste(utm, "severno"))
} else{
print(paste(utm , "južno"))
}
}
lonlat2UTMzone(c(21,45))
# [1] "34 severno"
lonlat2UTMzone(c(0,45))
# [1] "31 severno"
lonlat2UTMzone(c(-7,45))
# [1] "29 severno"
lonlat2UTMzone(c(-179,-45))
# [1] "1 južno"Dakle, sve formule koje važe za računanje koordinata u Gaus-Krigerovoj projekciji važe i u UTM projekciji u zoni od \(84^o\) severne geodetske širine do \(80^o\) južne geo. širine, uz sledeće modifikacije:
Razmera duž srednjeg meridijana je m0=0.9996.
Yo = 500 000, Xo = 0 (Xo = 10 000 000 – za Južnu hemisferu)
8.1 Direktni zadatak (grupisane formule)
Ako se dalje uvedu uobičajene oznake, možemo definisati konačne grupisane formule za direktni zadatak čije je izvođenje objašnjeno u prethodnom poglavlju za Gaus-Krigerovu projekciju:
\[ \begin{aligned} x= &x(\varphi, \lambda)= 0.9996 [\bar{X}(\varphi)+A_2(\varphi) \cdot l^2+A_4(\varphi) \cdot l^4+A_6(\varphi) \cdot l^6] \\ y= &y(\varphi, \lambda)= 500000 + 0.9996 [A_1(\varphi) \cdot l+A_3(\varphi) \cdot l^3+A_5(\varphi) \cdot l^5] \end{aligned} \]
Formulu za dužinu meridijanskog luka smo definisali ranije (dobro je napisati ponovo uz grupisane formule):
\[ \begin{aligned} &\bar{X}(\varphi)=a \cdot\left(1-e^2\right) \cdot\left(A \cdot \varphi-\frac{B}{2} \cdot \sin (2 \cdot \varphi)+\frac{C}{4} \cdot \sin (4 \cdot \varphi)-\frac{D}{6} \cdot \sin (6 \cdot \varphi)\right) \\ & A=1+\frac{3}{4} e^2+\frac{45}{64} e^4+\frac{175}{256} e^6+\ldots \\ & B=\frac{3}{4} e^2+\frac{15}{16} e^4+\frac{525}{512} e^6+\ldots \\ & C=\quad \frac{15}{64} e^4+\frac{105}{256} e^6+\ldots \\ & D=\quad \frac{35}{256} e^6+\ldots \end{aligned} \]
\[ l=\lambda-\lambda s r \]
\[ t(\varphi)=\operatorname{tan}(\varphi) \] \[ \eta(\varphi)=e_1 \cdot \cos (\varphi) \] \[ e_1^2 = e^{\prime 2}= \frac{a^2-b^2}{b^2} \]
\[ N=\frac{a}{\sqrt{\left(1-e^2 \sin (\varphi)^2\right)}} \]
\[ e^2=1-\frac{b^2}{a^2} \]
\[ \begin{aligned} &A_1=N(\varphi) \cdot \cos (\varphi) \\ & A_2=N(\varphi) \cdot \sin (\varphi) \cdot \frac{\cos (\varphi)}{2} \\ & A_3=N(\varphi) \cdot \cos (\varphi)^3 \cdot \frac{1+\eta(\varphi)^2-t(\varphi)^2}{6}\\ & A_4=N(\varphi) \cdot \sin (\varphi) \cdot \cos (\varphi)^3 \cdot \frac{5-t(\varphi)^2+9 \cdot \eta(\varphi)^2+4 \cdot \eta(\varphi)^4}{24} \\ & A_5=N(\varphi) \cdot \cos (\varphi)^5 \cdot \frac{5-18 \cdot t(\varphi)^2+t(\varphi)^4+14 \cdot \eta(\varphi)^2-58 \cdot \eta(\varphi)^2 \cdot t(\varphi)^2}{120} \\ & A_6=N(\varphi) \cdot \sin (\varphi) \cdot \cos (\varphi)^5 \cdot \frac{61-58 \cdot t(\varphi)^2+t(\varphi)^4}{720} \end{aligned} \]
Linearna razmera se računa po formuli:
\[ \begin{aligned} C_1 & =\frac{\cos ^2 \varphi}{2 \rho^2}\left(1+\eta^2\right) \\ C_2 & =\frac{\cos ^4 \varphi}{24 \rho^4}\left(5-4 t^2\right)\\ c& =m_0 (1+C_1 l^2+C_2 l^4)\\ c&= 0.9996 (1+C_1 l^2+C_2 l^4) \end{aligned} \]
Sledeća karta prikazuje elipse deformacija sa sračunatom linearnom deformacijom u dm po km, Slika 8.3.
library(sf)
# kreiramo tačke u kojima cemo prikazati elipse deformacija
lonlat = rbind(c(19,42), c(19,44), c(19,46),
c(20,42), c(20,44), c(20,46),
c(21,42), c(21,44), c(21,46),
c(22,42), c(22,44), c(22,46) ,
c(23,42), c(23,44), c(23,46) )
tissot.pt <- st_sfc( st_multipoint(lonlat),
crs = 4326) # WGS84 koordinatni ref. sis.
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# koristi se s2 paket za elipsodna računanja
# Pravimo tacke po krugu udaljene 30 km od centra elipse
tissot.sf = st_buffer(tissot.pt, dist = 30000, max_cells = 1000)
# max_cells
# The maximum number of cells to approximate a buffer.
# nrow(st_coordinates(tissot.sf[1]))
# [1] 646
# Ako koristimo opciju max_cell = 1000 imamo 646 prelomnih tačaka poligona
# konvertujemo kolekciju poligona u sf objekat
tissot.sf <- st_sf(tissot.sf)
tissot.utm <- st_transform(tissot.sf, "+proj=utm +zone=34 +ellps=GRS80")
lr <- function(lonlatmatrica){
l= (lonlatmatrica[,1] -21)*pi/180
fi= (lonlatmatrica[,2])*pi/180
# GRS80 a=6378137.0 rf=298.257222101 GRS 1980(IUGG, 1980)
a=6378137.0
rf=298.257222101
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
t=tan(fi)
eta=e1*cos(fi)
C1=1/2*(1+eta^2)*(cos(fi))^2
C2=1/24*(5-4*t^2)*(cos(fi))^4
# linerarna razmera (u R-u se uglavnom ne koristi c kao promenljiva)
cc=0.9996*(1+C1*l^2+C2*l^4)
return(cc)
}
# linerarna deformacija u dm/km
tissot.utm$dc <- (lr(lonlat)-1) *1000*10
url=paste('http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs',
'?service=WFS&version=1.0.0&',
'request=GetFeature&typeName=osgl_4:POP_age',sep='')
download.file(url, 'poage.gml')
pop = st_read('poage.gml')
# Reading layer `POP_age' from data source `C:\mk_knjiga\poage.gml' using driver `GML'
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# CRS: NA
st_crs(pop) = 4326
pop = st_transform(pop, "+proj=utm +zone=34 +ellps=GRS80")
ll = st_centroid(tissot.utm)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
# Karta sa elipsama deformacija i deformacijom dužina dm/km
plot(st_geometry(pop), graticule = TRUE, col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.utm),
border = rgb(44/255,127/255,184/255,0.5),
col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste("dc=",round(tissot.utm$dc,2)) ,col='red' , cex = 0.8)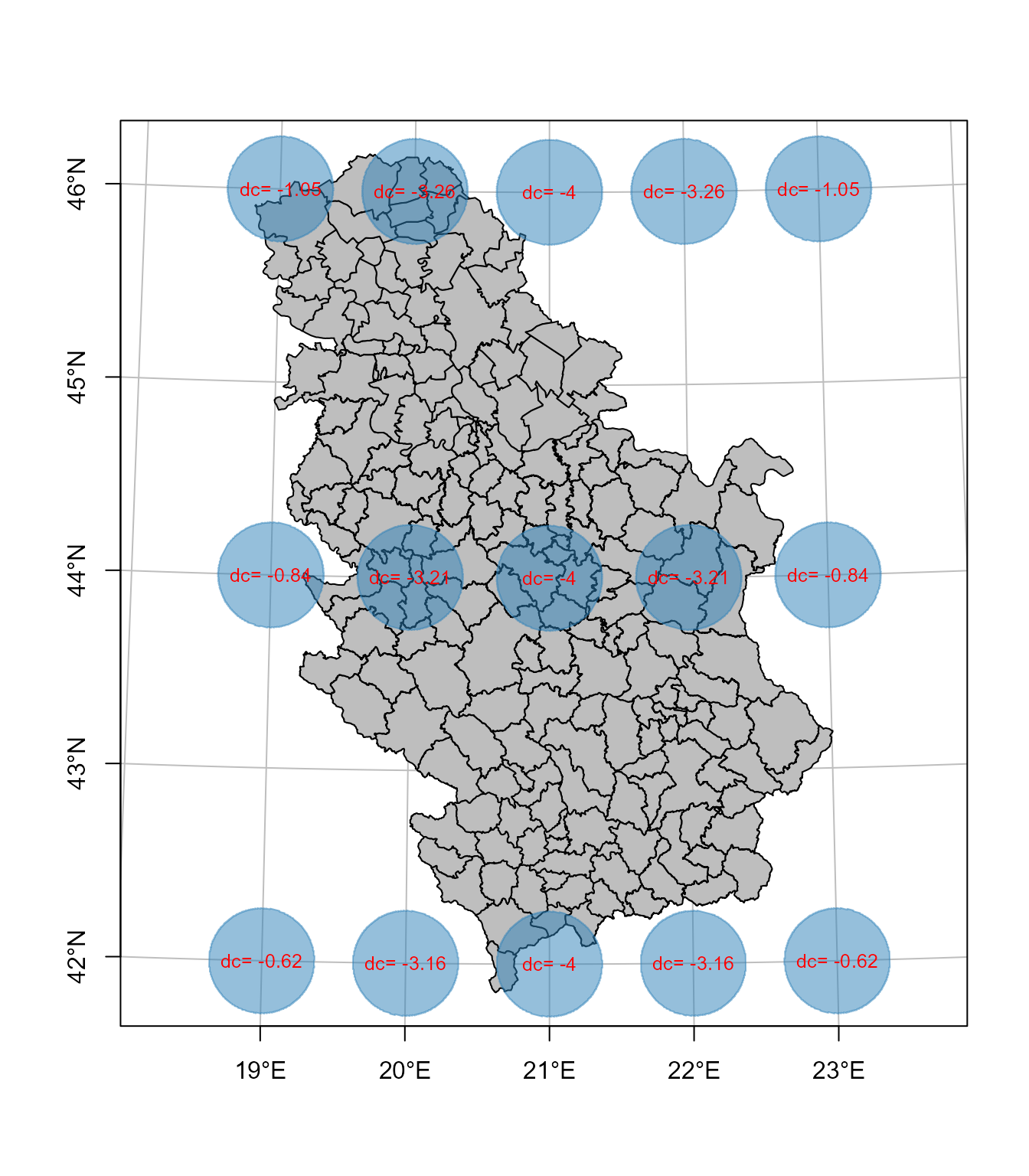
8.2 Inverzni zadatak
Formule se mogu zapisati i u obliku:
\[ \begin{gathered} \varphi=\varphi_1-B_2 y^2+B_4 y^4-B_6 y^6 \\ l=B_1 y-B_3 y^3+B_5 y^5 \end{gathered} \]
Pri čemu se \(\varphi_1\) može sračunati kao (Snyder (1987)):
\[ \begin{aligned} &\begin{aligned} \varphi_1= & \mu+\left(3 e_2 / 2-27 e_2^3 / 32+\ldots\right) \sin 2 \mu+\left(21 e_2^2 / 16\right. \\ & \left.-55 e_2^4 / 32+\ldots\right) \sin 4 \mu+\left(151 e_2^3 / 96+\ldots\right) \sin 6 \mu+\left(1097 e_2^4 / 512-\ldots\right) \\ & \sin 8 \mu+\ldots \end{aligned}\\ &\begin{aligned} & e_2=\left[1-\left(1-e^2\right)^{1 / 2}\right] /\left[1+\left(1-e^2\right)^{1 / 2}\right] \\ & \mu= L_m /\left[a\left(1-e^2 / 4-3 e^4 / 64-5 e^6 / 256-\ldots\right)\right] \\ & L_m=\bar{X}(\varphi_0)+y / m_0 \\ & \text{gde je } m_0 \text{ razmera duž sr. mer. za izvornu GK } m_0 = 1 , \\ &\text{za Srbiju } m_0 = 0.9999, \\ &\text{za UTM } m_0 = 0.9996. \end{aligned} \end{aligned} \]
Neophodan je iterativni postupak koji brzo konvergira od \(\varphi_0\) do \(\varphi_1\).
\[
\begin{gathered}
B_1=\frac{\rho}{N_1 \cos \varphi_1} \\
B_2=\frac{\rho}{2 M_1 N_1} t_1 \\
B_3=\frac{\rho}{6 N_1^3 \cos \varphi_1}\left(1+2 t_1^2+\eta_1^2\right) \\
B_4=\frac{p}{24 M_1 N_1^3} t_1\left(5+3 t_1^2+n_1^2-9 n_1^2 t_1^2\right) \\
B_5=\frac{\rho}{120 N_1^5 \cos \varphi_1}\left(5+28 t_1^2+24 t_1^4+6 \eta_1^2+8 \eta_1^2 t_1^2\right) \\
B_6=\frac{\rho}{720 M_1 N_1^5} t_1\left(61+90 t_1^2+45 t_1^4\right)
\end{gathered}
\] UTM projekcija za Srbiju definisana je sledećim oblikom u proj4 notaciji:
+proj=utm +zone=34 +ellps=GRS80 +towgs84=0.26901,0.18246,0.06872,-0.01017,0.00893,-0.01172,0.04 +units=mPošto je geometrija GRS80 elipsoida skoro identična kao WGS84, a i datum je takav da se skoro poklapa sa WGS84, često imamo definisanu UTM projekciju za Srbiju na sledeći način:
+proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crsIli još jednostavnije:
+proj=utm +zone=34 +datum=WGS84 +units=m +no_defsUTM EPSG kodovi se kreću uzastopno od 32601 do 32660 za lokacije na severnoj hemisferi i od 32701 do 32760 za lokacije na južnoj hemisferi. Tako da se može napraviti kod za definisanje epsg notacije UTM koordinatnog sistema (Lovelace, Nowosad, and Muenchow (2019)).
library(sf)
lonlat2UTM = function(lonlat) {
utm = (floor((lonlat[1] + 180) / 6) %% 60) + 1
if(lonlat[2] > 0) {
utm + 32600
} else{
utm + 32700
}
}
# tačka u Srbiji
(sr=lonlat2UTM(c(21,45)) )
# [1] 32634
st_crs(sr)$proj4string
# [1] "+proj=utm +zone=34 +datum=WGS84 +units=m +no_defs"
# tačka u UK
(gb =lonlat2UTM(c(0,45)) )
# [1] 32631
st_crs(gb)$proj4string
# [1] "+proj=utm +zone=31 +datum=WGS84 +units=m +no_defs"8.3 Značaj UTM projekcije
UTM je jedna od najznačajnijih kartografskih projekcija, uključujući i UTM koordinatni sistem koji su prvobitno razvili vojni geodeti sredinom 20. veka. Od tada je UTM sistem postao naširoko korišćen za katastarske radove i kartografske radove krupne razmere kao što su radovi vezani za Osnovnu državnu kartu (ODK), fotogrametriju i daljinsku detekciju. Popularnost UTM-a može se pripisati relativno malim deformacijama, omogućavajući precizno georeferenciranje slika za potrebe fotogrametrije i daljinske detekcije, kao i za preciznu navigaciju. Trenutno, UTM se koristi u raznim institucijama kao što su NASA, NOAA, JAKSA, ISRO za distribuciju različitih proizvoda sa satelitskih snimaka. Dva značajna programa koji koriste UTM sistem su Landsat (USA) enterprise i Copernicus Sentinel-2 kojima upravlja Evropska unija, a oba se odnose na satelitske misije čiji su podaci besplatni, a isporučuju multispektralne snimke Zemlje srednje rezolucije (Bauer-Marschallinger and Falkner 2023).
8.4 Primeri u UTM projekciji
Primer 1: Računanje koordinata jedne tačke, direktni zadatak
Elipsoidne koordinate pozicije Građevinskog fakulteta u Beogradu (\(\varphi=44.8057705\) i \(\lambda=20.4759749\)) iz koordinatnog sistema WGS84 transformisati u UTM projekciju.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = st_point( c(20.4759749, 44.8057705) ) # lon , lat
# potom pravimo kolekciju geometrije sfc u odgovarajućoj projekciji
pts_sfc = st_sfc(grf, crs=4326) #epsg 4326 je WGS84 long lat
# UTM Srb koord. ref. sis.
utm_srb = "+proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs"
# transformacija u UTM
pts_sfc_utm = st_transform(pts_sfc, crs =utm_srb)
pts_sfc_utm
# Geometry set for 1 feature
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: 458559.50217 ymin: 4961507.88131 xmax: 458559.50217 ymax: 4961507.88131
# Projected CRS: +proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs
# matrica koordinata iz prostornih podataka
st_coordinates(pts_sfc_utm)
# X Y
# [1,] 458559.50217 4961507.88131
# koordinate treba zaokružiti do na cm
round(st_coordinates(pts_sfc_utm),2)
# X Y
# [1,] 458559.5 4961507.88
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import shapely.geometry
import geopandas as gpd
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = shapely.geometry.Point(20.4759749 , 44.8057705)
# potom pravimo kolekciju geometrije sa koor. ref.sis
grf_geom_proj = gpd.GeoSeries([grf], crs=4326) #epsg 4326 je WGS84 long lat
# prostorni lejer
grf_layer_proj = gpd.GeoDataFrame({'geometry': grf_geom_proj})
# utm Srb koord. ref. sis.
utm_srb = "+proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs"
# transformacija u utm projekciju
grf=grf_layer_proj.to_crs(utm_srb)
print(grf)
# geometry
# 0 POINT (458559.502 4961507.881)Primer 2: Grafik deformacija u zavisnosti od geodetske dužine za fiksiranu geodetsku širinu
Napraviti grafik deformacije dužina izražene u dm/km u zavisnosti od geodetske dužine za fiksiranu geodetsku širinu na \(\varphi=43^o\) u UTM projekciji.
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
fi = 43*pi/180
# redukovane širine za koje računamo deformacije
l=(seq(18,24,by=0.2) -21)*pi/180
# GRS80 a=6378137.0 rf=298.257222101 GRS 1980(IUGG, 1980)
a=6378137.0
rf=298.257222101
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
t=tan(fi)
eta=e1*cos(fi)
C1=1/2*(1+eta^2)*(cos(fi))^2
C2=1/24*(5-4*t^2)*(cos(fi))^4
# linerarna razmera (u R-u se uglavnom ne koristi c kao promenljiva)
cc=0.9996*(1+C1*l^2+C2*l^4)
# linerarna deformacija
dc=cc-1
# linerarna deformacija u dm/km
dc_dm_km = round( dc *1000*10 ,1)
plot(21+l*180/pi ,dc_dm_km, main = "Lin. def. u zavisnosti od geod. duž.",
xlab = parse(text = "lambda"),
ylab = "Linearna deformacija u dm/km",type = "l")
grid()
import numpy as np
import matplotlib.pyplot as plt
fi = 43 * np.pi / 180
# redukovana geod. dužina
l = (np.arange(18, 24, 0.2) - 21) * np.pi / 180
# GRS80 a=6378137.0 rf=298.257222101 GRS 1980(IUGG, 1980)
a=6378137.0
rf=298.257222101
f = 1 / rf
e = np.sqrt(2 * f - f ** 2)
e1 = np.sqrt((2 * f - f ** 2) * (1 - f) ** -2)
# b = 6356078.9628181880963
# e1 = np.sqrt((a ** 2 - b ** 2) / b ** 2)
t = np.tan(fi)
eta = e1 * np.cos(fi)
C1 = 1 / 2 * (1 + eta ** 2) * (np.cos(fi)) ** 2
C2 = 1 / 24 * (5 - 4 * t ** 2) * (np.cos(fi)) ** 4
# linearna razmera
c= 0.9999 * (1 + C1 * l ** 2 + C2 * l ** 4)
# linearna deformacija
dc = c - 1
# linearna deformocija dm/km
dc_dm_km = np.round(dc * 1000 * 10, 1)
plt.plot(21 + l * 180 / np.pi, dc_dm_km)
plt.title("Lin. def. u zavisnosti od geod. duž.")
plt.xlabel(r"$\lambda$")
plt.ylabel("Linearna deformacija u dm/km")
plt.grid()
plt.show()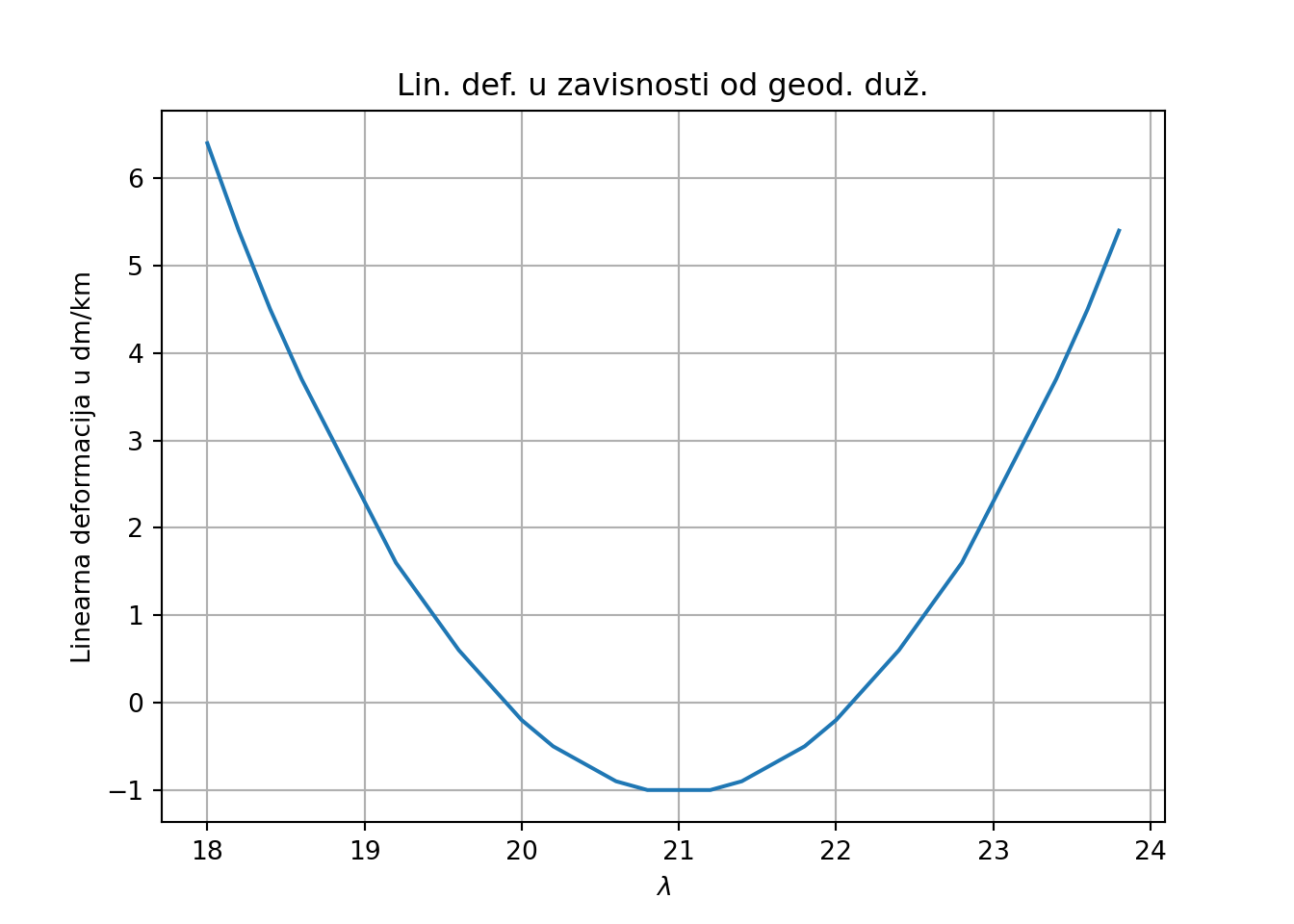
Primer 3: Napraviti kartu izokola u UTM projekciji
Napraviti kartu izokola, sa vrednostima deformacija dužina izraženim u dm/km u UTM projekciji za Srbiju.
library(terra)
bbox= ext(c(18.81499446, 23.00637464, 41.85209979, 46.19005677 ) )
#(xmin, xmax, ymin, ymax)
# prazan raster
er <- rast(bbox, resolution=0.00833 )
# 0.00833 * 6377000*pi/180 oko 1 km rezolucija
# koordinate za svaki piksel rastera
l <- ( init(er, 'x') -21) *pi/180
fi <- init(er, 'y') *pi/180
# GRS80 a=6378137.0 rf=298.257222101 GRS 1980(IUGG, 1980)
a=6378137.0
rf=298.257222101
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
# b=6356078.9628181880963
# e1= sqrt((a^2-b^2)/b^2)
t=tan(fi)
eta=e1*cos(fi)
C1=1/2*(1+eta^2)*(cos(fi))^2
C2=1/24*(5-4*t^2)*(cos(fi))^4
# linerarna razmera (u R-u se uglavnom ne koristi c kao promenljiva)
cc=0.9996*(1+C1*l^2+C2*l^4)
# linerarna deformacija
dc=cc-1
# linerarna deformacija u dm/km
dc_dm_km = round( dc *1000*10 ,1)
plot(dc_dm_km, main="Izokole, deformacije dužina dm/km")
contour(dc_dm_km, add=TRUE, nlevels = 15)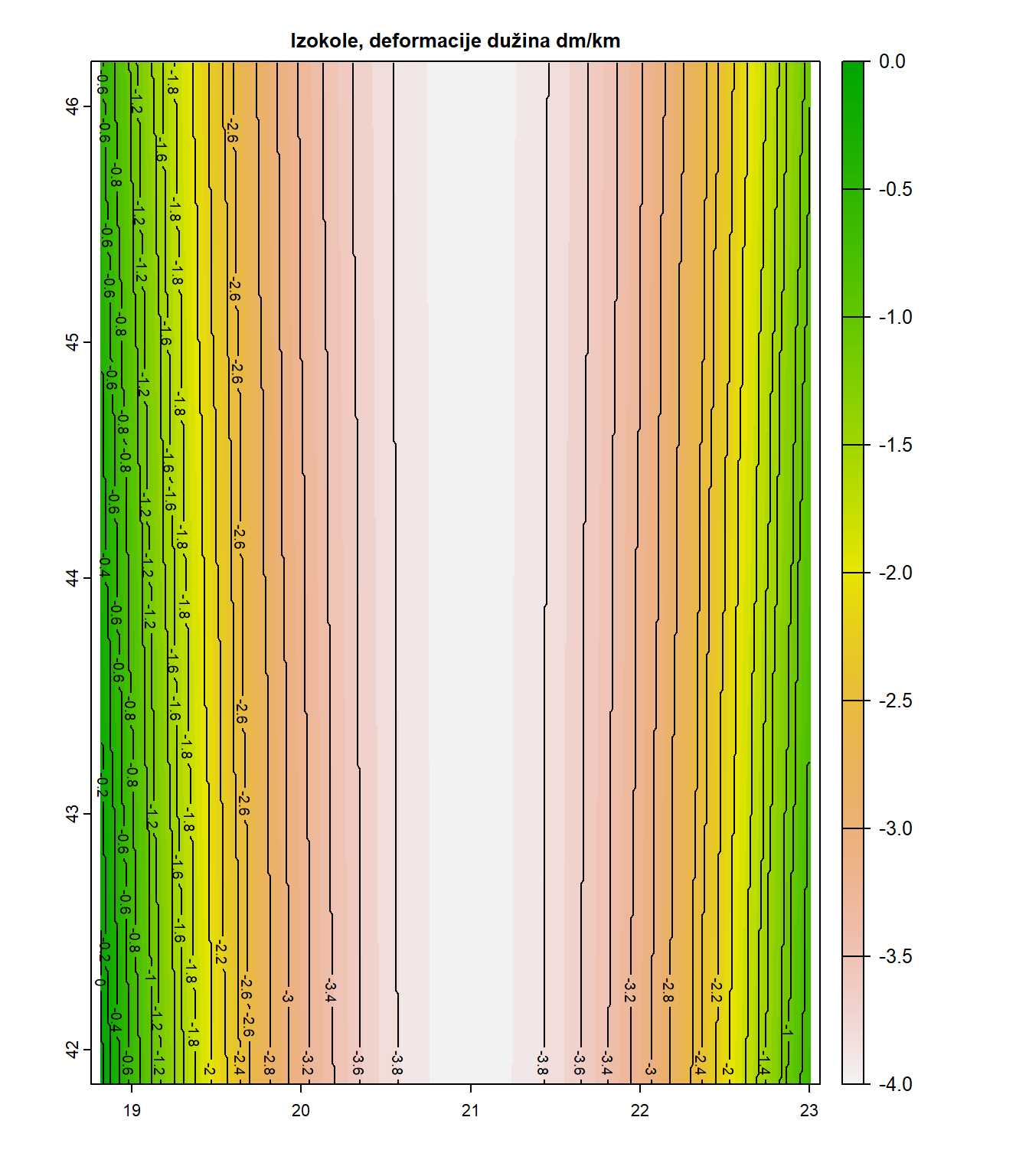
import numpy as np
import rasterio
from rasterio.plot import show
import matplotlib.pyplot as plt
import os
# okvir
bbox = (18.81499446, 23.00637464, 41.85209979, 46.19005677)
# raster sa zadatom rezolucijom
resolution = 0.00833
width = int((bbox[1] - bbox[0]) / resolution)
height = int((bbox[3] - bbox[2]) / resolution)
transform = rasterio.transform.from_origin(bbox[0], bbox[3], resolution, resolution)
er = np.zeros((height, width))
height = er.shape[0]
width = er.shape[1]
cols, rows = np.meshgrid(np.arange(width), np.arange(height))
xs, ys = rasterio.transform.xy(transform, rows, cols)
lons= np.array(xs)
lats = np.array(ys)
# lon lat matrice
l = (lons - 21) * np.pi / 180
fi = lats * np.pi / 180
# GRS80 a=6378137.0 rf=298.257222101 GRS 1980(IUGG, 1980)
a=6378137.0
rf=298.257222101
f = 1 / rf
e = np.sqrt(2 * f - f ** 2)
e1 = np.sqrt((2 * f - f ** 2) * (1 - f) ** -2)
t = np.tan(fi)
eta = e1 * np.cos(fi)
C1 = 1 / 2 * (1 + eta ** 2) * (np.cos(fi)) ** 2
C2 = 1 / 24 * (5 - 4 * t ** 2) * (np.cos(fi)) ** 4
# linearna razmera
cc = 0.9996 * (1 + C1 * l ** 2 + C2 * l ** 4)
# linearna deformacija
dc = cc - 1
# linearna deformacija dm po km
dc_dm_km = np.round(dc * 1000 * 10, 1)
rio_arr = rasterio.open('tmp2.tif',driver='GTiff', mode='w',
height=height,
width=width,
count=1,
dtype=dc_dm_km.dtype,
transform=transform)
rio_arr.write(dc_dm_km,1)
rio_arr.close()
rio_arr = rasterio.open('tmp2.tif')
fig, ax = plt.subplots()
show(rio_arr, ax =ax, cmap="terrain")
show(rio_arr, contour=True,ax=ax, colors="black")
plt.show()
# os.remove("tmp2.tif")Primer 4: Transformacija vektorskih podataka iz WGS84 u UTM (DKS)
Transformisati poligone opština u Srbiji u UTM DKS. Poligoni opština se mogu preuzeti kroz WFS servis laboratorije za razvoj softvera otvorenog koda na Građevinskom fakultetu, OSGL Beograd.
library(sf)
# granice opština u Srb
url=paste('http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs',
'?service=WFS&version=1.0.0&',
'request=GetFeature&typeName=osgl_4:POP_age',sep='')
download.file(url, 'poage.gml')
pop = st_read('poage.gml')
# Reading layer `POP_age' from data source `C:\mk_knjiga\poage.gml' using driver `GML'
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# CRS: NA
st_crs(pop) = 4326
pop
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# Geodetic CRS: WGS 84
# First 10 features:
# gml_id ID_Municip NameASCII NameLatin Area SHAPE_Leng
# 1 POP_age.1 70335 Bosilegrad Bosilegrad 571273097 121715
# 2 POP_age.2 80195 Kanjiza Kanji�a 398623963 94729
# 3 POP_age.3 80438 Subotica Subotica 100734608 164832
# 4 POP_age.4 70572 Kladovo Kladovo 627254771 137660
# 5 POP_age.5 80454 Titel Titel 260745278 104386
# 6 POP_age.6 80110 Becej Becej 486479140 130561
# 7 POP_age.7 80268 Novi Becej Novi Becej 608393938 157111
# 8 POP_age.8 80136 Zabalj �abalj 399798048 127101
# 9 POP_age.9 80390 Srbobran Srbobran 284106212 89115
# 10 POP_age.10 80152 Zrenjanin Zrenjanin 132585270 272176
# SHAPE_Area NUTS0 NUTS1 NUTS2 NUTS3 TOTAL_POP ADULTS AVARAGE
# 1 5.71e+08 RS RS2 RS22 RS228 8129 6843 45.1774511
# 2 3.98e+08 RS RS1 RS12 RS124 25343 20842 42.44057531
# 3 1.01e+09 RS RS1 RS12 RS125 141554 116545 41.90601467
# 4 6.27e+08 RS RS2 RS22 RS221 20635 17644 46.75699055
# 5 2.61e+08 RS RS1 RS12 RS123 15738 12747 41.21559283
# 6 4.86e+08 RS RS1 RS12 RS123 37351 30217 41.47866188
# 7 6.08e+08 RS RS1 RS12 RS126 23925 19566 41.50948798
# 8 4.00e+08 RS RS1 RS12 RS123 26134 20616 39.71022423
# 9 2.84e+08 RS RS1 RS12 RS123 16317 13189 41.12824049
# 10 1.33e+09 RS RS1 RS12 RS126 123362 101780 42.19447642
# the_geom
# 1 MULTIPOLYGON (((22.3 42.6, ...
# 2 MULTIPOLYGON (((19.9 46.2, ...
# 3 MULTIPOLYGON (((19.7 46.2, ...
# 4 MULTIPOLYGON (((22.5 44.7, ...
# 5 MULTIPOLYGON (((20.2 45.3, ...
# 6 MULTIPOLYGON (((20.1 45.7, ...
# 7 MULTIPOLYGON (((20.3 45.8, ...
# 8 MULTIPOLYGON (((20.1 45.5, ...
# 9 MULTIPOLYGON (((20.1 45.5, ...
# 10 MULTIPOLYGON (((20.4 45.6, ...
utm_srb = "+proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs"
pop = st_transform(pop,utm_srb)
pop
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 331000 ymin: 4630000 xmax: 663000 ymax: 5120000
# Projected CRS: +proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs
# First 10 features:
# gml_id ID_Municip NameASCII NameLatin Area SHAPE_Leng
# 1 POP_age.1 70335 Bosilegrad Bosilegrad 571273097 121715
# 2 POP_age.2 80195 Kanjiza Kanji�a 398623963 94729
# 3 POP_age.3 80438 Subotica Subotica 100734608 164832
# 4 POP_age.4 70572 Kladovo Kladovo 627254771 137660
# 5 POP_age.5 80454 Titel Titel 260745278 104386
# 6 POP_age.6 80110 Becej Becej 486479140 130561
# 7 POP_age.7 80268 Novi Becej Novi Becej 608393938 157111
# 8 POP_age.8 80136 Zabalj �abalj 399798048 127101
# 9 POP_age.9 80390 Srbobran Srbobran 284106212 89115
# 10 POP_age.10 80152 Zrenjanin Zrenjanin 132585270 272176
# SHAPE_Area NUTS0 NUTS1 NUTS2 NUTS3 TOTAL_POP ADULTS AVARAGE
# 1 5.71e+08 RS RS2 RS22 RS228 8129 6843 45.1774511
# 2 3.98e+08 RS RS1 RS12 RS124 25343 20842 42.44057531
# 3 1.01e+09 RS RS1 RS12 RS125 141554 116545 41.90601467
# 4 6.27e+08 RS RS2 RS22 RS221 20635 17644 46.75699055
# 5 2.61e+08 RS RS1 RS12 RS123 15738 12747 41.21559283
# 6 4.86e+08 RS RS1 RS12 RS123 37351 30217 41.47866188
# 7 6.08e+08 RS RS1 RS12 RS126 23925 19566 41.50948798
# 8 4.00e+08 RS RS1 RS12 RS123 26134 20616 39.71022423
# 9 2.84e+08 RS RS1 RS12 RS123 16317 13189 41.12824049
# 10 1.33e+09 RS RS1 RS12 RS126 123362 101780 42.19447642
# the_geom
# 1 MULTIPOLYGON (((605874 4716...
# 2 MULTIPOLYGON (((418426 5114...
# 3 MULTIPOLYGON (((397325 5115...
# 4 MULTIPOLYGON (((616554 4952...
# 5 MULTIPOLYGON (((434680 5019...
# 6 MULTIPOLYGON (((426835 5066...
# 7 MULTIPOLYGON (((446663 5070...
# 8 MULTIPOLYGON (((429591 5041...
# 9 MULTIPOLYGON (((426109 5039...
# 10 MULTIPOLYGON (((451617 5050...
# Karta opština u Merkatorovoj projekciji
plot(st_geometry(pop), graticule = TRUE, border = 'grey', axes = TRUE)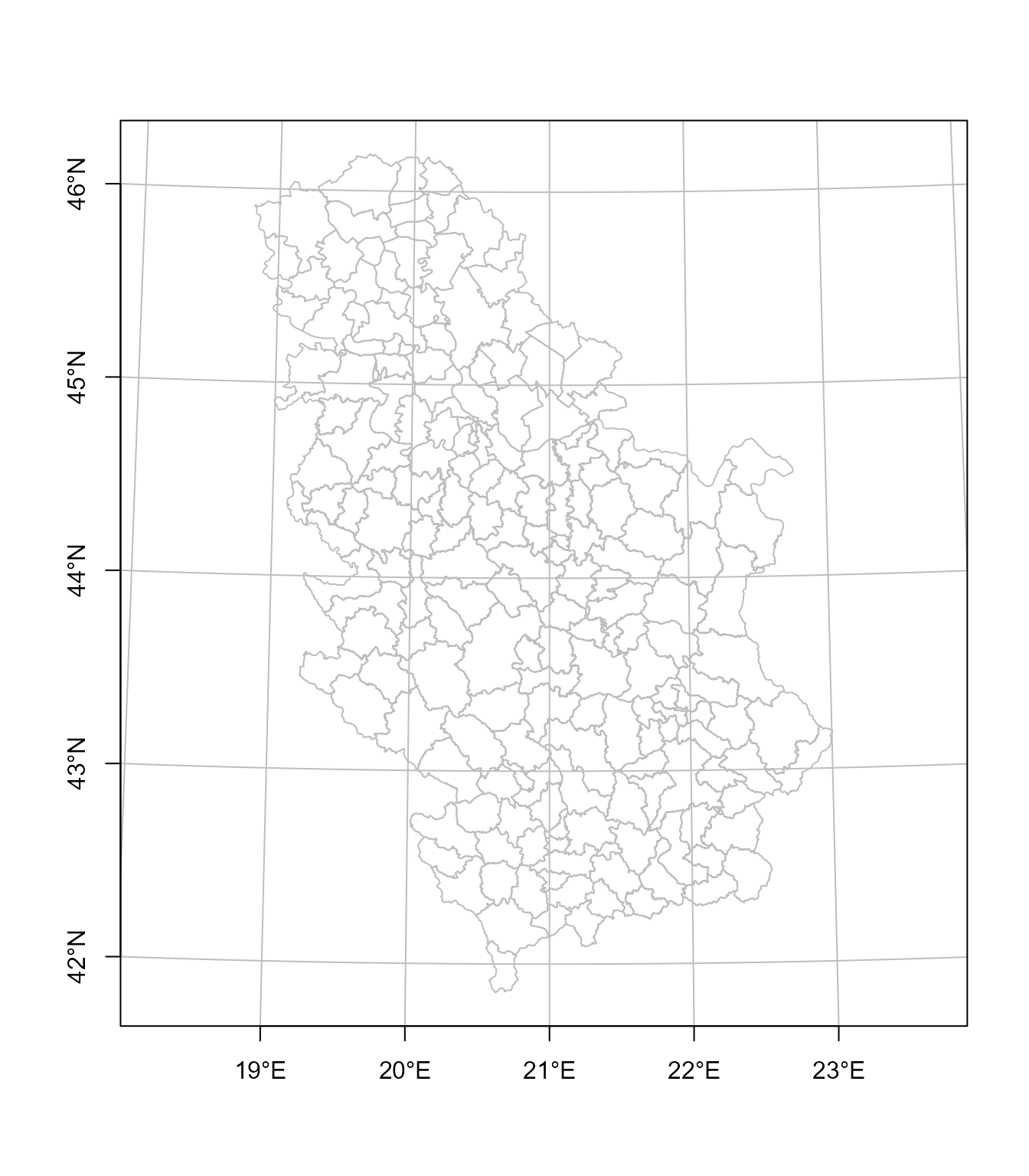
import geopandas as gpd
import matplotlib.pyplot as plt
import requests
# granice opština u Srb
url = 'http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs' + \
'?service=WFS&version=1.0.0&request=GetFeature&typeName=osgl_4:POP_age'
response = requests.get(url)
# snimamo fajl na disk
open('data/pop.gml', 'wb').write(response.content)
# 9461553
gdf = gpd.read_file('data/pop.gml')
# Podaci su u WGS84 (EPSG:4326)
gdf.crs = 'epsg:4326'
gdf
# gml_id ... geometry
# 0 POP_age.1 ... MULTIPOLYGON (((22.29045 42.59307, 22.29047 42...
# 1 POP_age.2 ... MULTIPOLYGON (((19.94315 46.17601, 19.94470 46...
# 2 POP_age.3 ... MULTIPOLYGON (((19.66958 46.18402, 19.66976 46...
# 3 POP_age.4 ... MULTIPOLYGON (((22.47150 44.71333, 22.47564 44...
# 4 POP_age.5 ... MULTIPOLYGON (((20.16648 45.32598, 20.16532 45...
# .. ... ... ...
# 192 POP_age.193 ... MULTIPOLYGON (((21.28057 42.44932, 21.28637 42...
# 193 POP_age.194 ... MULTIPOLYGON (((21.56451 42.73154, 21.56464 42...
# 194 POP_age.195 ... MULTIPOLYGON (((21.46112 42.62940, 21.46216 42...
# 195 POP_age.196 ... MULTIPOLYGON (((20.59400 42.88168, 20.60346 42...
# 196 POP_age.197 ... MULTIPOLYGON (((19.54257 44.48493, 19.54272 44...
#
# [197 rows x 15 columns]
# transformišemo u UTM DKS projekciju
utm_srb = "+proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs"
gdf = gdf.to_crs(utm_srb)
gdf
# gml_id ... geometry
# 0 POP_age.1 ... MULTIPOLYGON (((605874.414 4716434.455, 605876...
# 1 POP_age.2 ... MULTIPOLYGON (((418425.863 5114147.074, 418545...
# 2 POP_age.3 ... MULTIPOLYGON (((397325.126 5115354.405, 397341...
# 3 POP_age.4 ... MULTIPOLYGON (((616553.529 4952159.059, 616885...
# 4 POP_age.5 ... MULTIPOLYGON (((434679.717 5019501.704, 434586...
# .. ... ... ...
# 192 POP_age.193 ... MULTIPOLYGON (((523071.728 4699703.932, 523550...
# 193 POP_age.194 ... MULTIPOLYGON (((546211.975 4731157.457, 546223...
# 194 POP_age.195 ... MULTIPOLYGON (((537810.303 4719764.642, 537896...
# 195 POP_age.196 ... MULTIPOLYGON (((466844.534 4747756.100, 467615...
# 196 POP_age.197 ... MULTIPOLYGON (((384107.167 4926768.123, 384118...
#
# [197 rows x 15 columns]
# Karta
ax = gdf.plot(edgecolor='grey', figsize=(10, 8))
ax.set_axis_on()
ax.set_xlabel('E')
ax.set_ylabel('N')
plt.grid(True)
plt.show()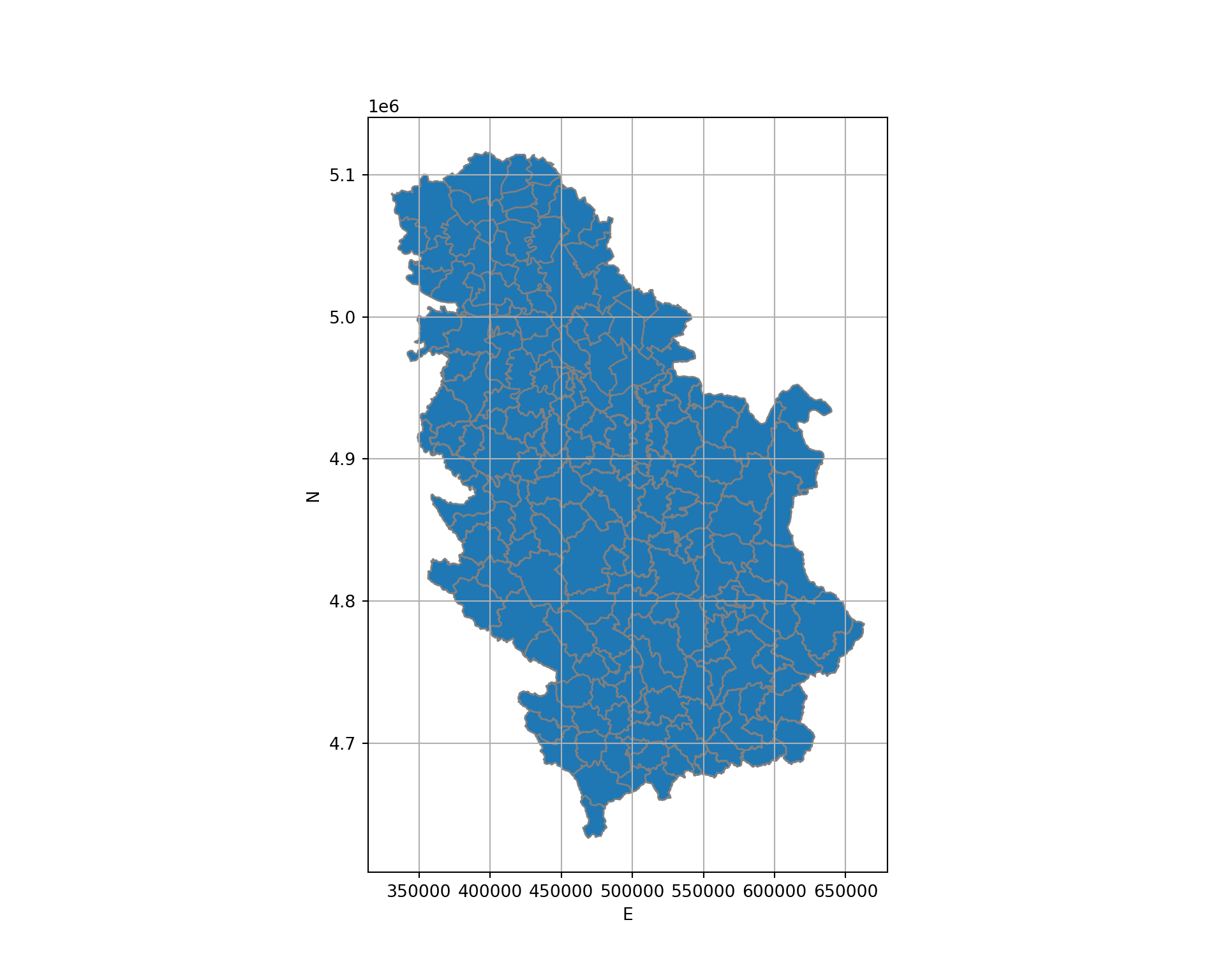
Primer 5: Inverzni zadatak UTM projekcija
Sračunati elipsoidne koordinate za tačke T1(523517.93, 4700608.49) i T2(384505.11, 4927736.75) zadate u UTM projekciji. Koordinate prikazati i u obliku stepen, minut i sekund.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Za tacke sa koordinatama T1(7523517.93, 4700608.49) i T2(7384505.11, 4927736.75)
# u utm DKS projekciji
utm_srb = "+proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs"
# tačke u projekciji
tutm= st_sfc( st_point(c(523517.93, 4700608.49)), st_point(c(384505.11, 4927736.75)),
crs = utm_srb )
# inverzni zadatak iz pravouglih u longitudu, latitudu
tLL = st_transform(tutm,
crs =4326)
ll = st_coordinates(tLL)
# Koordinate treba zaokružiti do na cm ili dm, što je oko 6. decimale
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
round(ll,6)
# X Y
# [1,] 21.286030 42.457454
# [2,] 19.547352 44.493710
# gedetska dužina i širina
# lon lat
lon = ll[,1]
lat = ll[,2]
# funkcija za stepen u stepen minut sekund
deg2dms <- function(deg){
deg_sign = sign(deg)
deg = abs(deg)
DEG = floor(deg)
MIN = floor((deg - DEG) * 60)
SEC = (deg - DEG - MIN/60) * 3600
SEC=round(SEC,2)
dms=paste(deg_sign*DEG,'\u00B0',MIN,"'",SEC,"''",sep='')
return(dms)
}
# gedetska dužina i širina
print(paste("T1 " ,deg2dms(lon[1]), deg2dms(lat[1])) )
# [1] "T1 21°17'9.71'' 42°27'26.83''"
print(paste( "T2 " ,deg2dms(lon[2]), deg2dms(lat[2])) )
# [1] "T2 19°32'50.47'' 44°29'37.36''"import shapely.geometry
import geopandas as gpd
# pravimo GeoDataFrame koordinate u LCC projekciji
data = {'geometry': [shapely.geometry.Point(523517.93, 4700608.49), shapely.geometry.Point(384505.11, 4927736.75)]}
utm_srb = "+proj=utm +zone=34 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs"
gdf = gpd.GeoDataFrame(data, crs=utm_srb) # utm_srb
# transformacija na bes_crs
gdf_bes = gdf.to_crs(4326)
print(gdf_bes)
# geometry
# 0 POINT (21.28603 42.45745)
# 1 POINT (19.54735 44.49371)
# Prikaz koordinata na 6 decimala
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
lon = gdf_bes["geometry"].x
lat = gdf_bes["geometry"].y
# gedetska dužina i širina
print("T1 " ,round(lon[0],6), round(lat[0],6))
# T1 21.28603 42.457454
print("T2 " ,round(lon[1],6), round(lat[1],6))
# T2 19.547352 44.49371
# funkcija za stepen u stepen minut sekund
def deg2dms(deg):
deg_sign = 1 if deg >= 0 else -1
deg = abs(deg)
DEG = int(deg)
MIN = int((deg - DEG) * 60)
SEC = (deg - DEG - MIN / 60) * 3600
SEC = round(SEC, 2)
dms = f"{deg_sign * DEG}\u00B0{MIN}'{SEC}''"
return dms
# gedetska dužina i širina
print(f"T1 {deg2dms(lon[0])} {deg2dms(lat[0])}")
# T1 21°17'9.71'' 42°27'26.83''
print(f"T2 {deg2dms(lon[1])} {deg2dms(lat[1])}")
# T2 19°32'50.47'' 44°29'37.36''