1 Uvod u kartografiju
Ovo poglavlje posvećeno je proučavanju ključnih elemenata kartografije koji čine osnovu za dublje razumevanje ove naučne discipline. Kroz sledeće sekcije istražićemo definiciju karte i kartografije. Prikazaćemo i istorijski razvoj kartografije. Potom od kojih podataka se prave karte, to su kartografski izvori. Pored toga, razmotrićemo važnost vektorskih i rasterskih podataka u procesu kreiranja karte i opisati osnovnu strukturu ovih podataka. Dalje, biće data podela kartografije, sa posebnim osvrtom na matematiču kartografiju, opisaćemo osnovne zadatke matematičke kartografije. Kroz osvrt na istoriju matematičke kartografije, osvetlićemo evoluciju matematičke kartografije kao oblasti.
1.1 Definicije karte
Iako postoji veliki broj definicija karte koje su formulisali različiti autori, ovde su predstavljene četiri, koje će adekvatno poslužiti potrebama ovog teksta.
Karta
Karta predstavlja apstrakciju i selekciju geografske realnosti, pri čemu su jasno izraženi prostorni oblici i odnosi.
Definicija 1: Karta je grafička reprezentacija kulturnog i fizičkog prostora. Ključna reč ovde je grafička reprezentacija jer su sve karte vizualna reprezentacija fenomena koji se modelira.
Definicija 2: Karta je redukovana, selektivna i simbolizovana grafička reprezentacija nekog prostora. Ova definicija uvodi tri ključna termina: redukovana, selektivna i simbolizovana. Prvi termin, redukovana, odnosi se na činjenicu da su skoro sve karte korisnije kada su izrađene u razmeri sitnijoj nego što je fenomen koji se kartira. Drugi termin, selektivne, znači da karte treba da uključe samo pojave koje su vezane za poruku karte. Treći termin, simbolizovana, odnosi se na ideju da se pojave na karti prikazuju korišćenjem kartografskih znakova ili simbola.
Definicija 3: Karta je savršeni interfejs između geoinformacija i njihovih korisnika (Georg Gartner, nekadašnji predsednik ICA). Drugim rečima, gledanjem u kartu ljudi su u stanju da posmatraju određeni prostor i njegove aspekte.
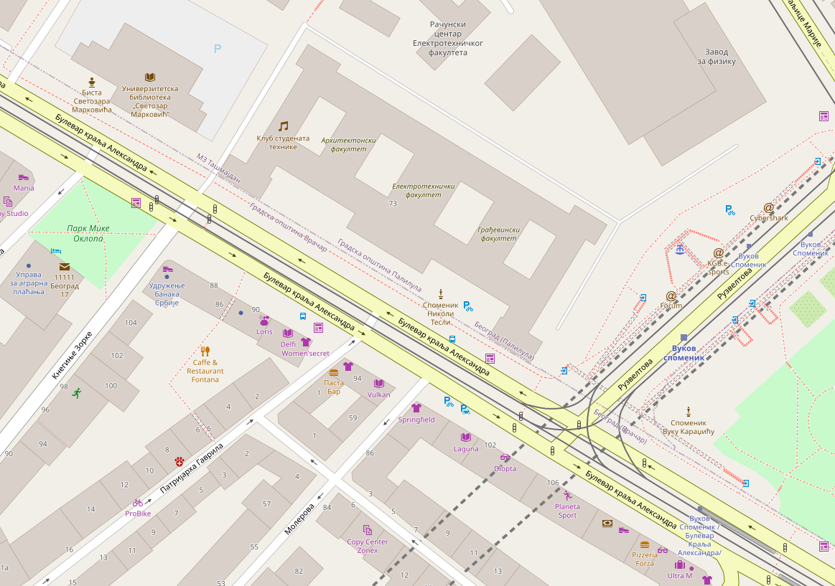
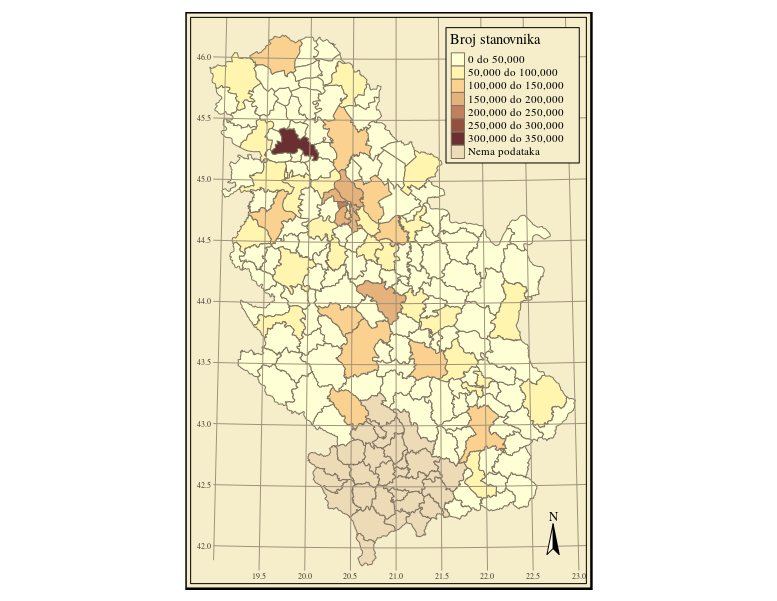
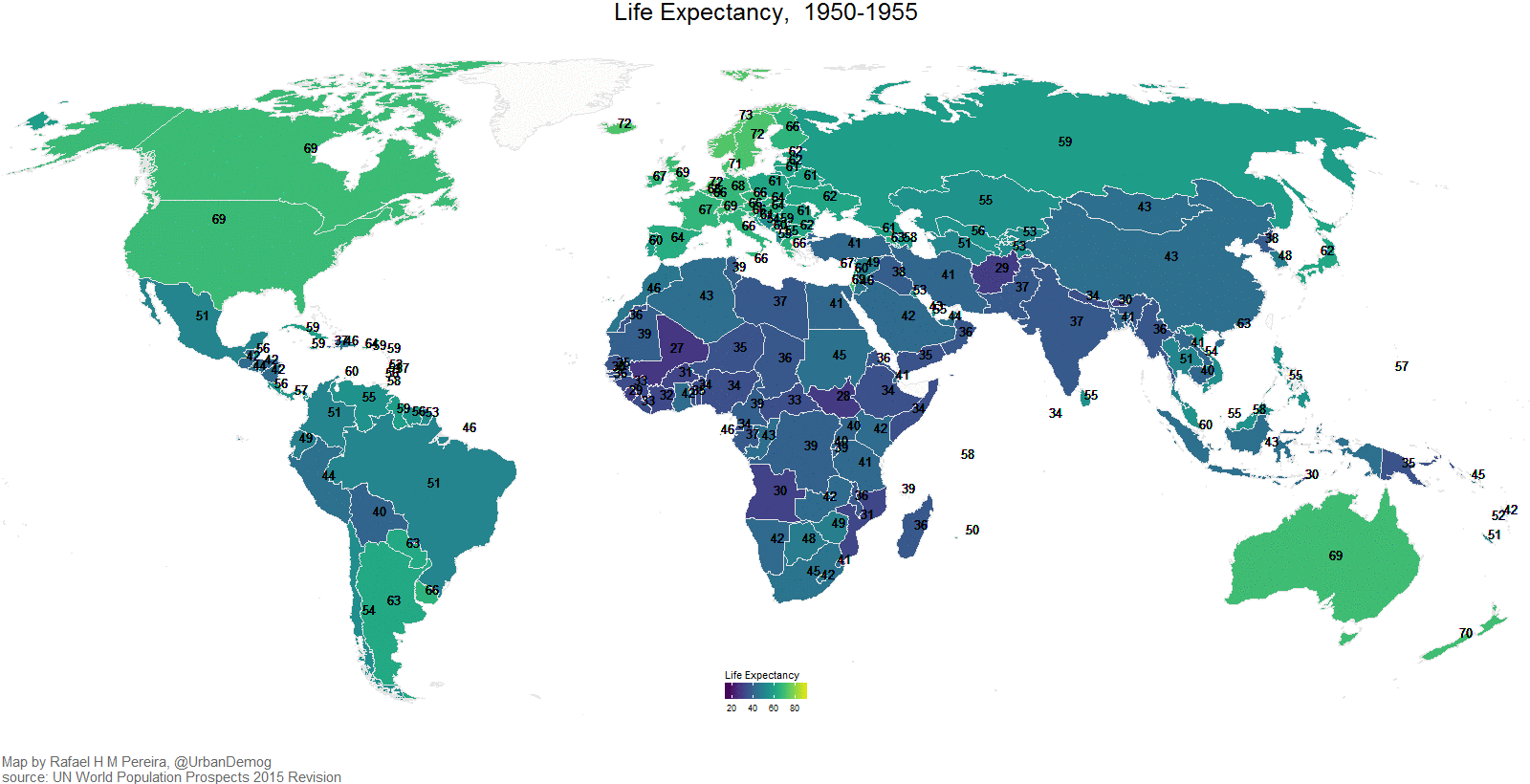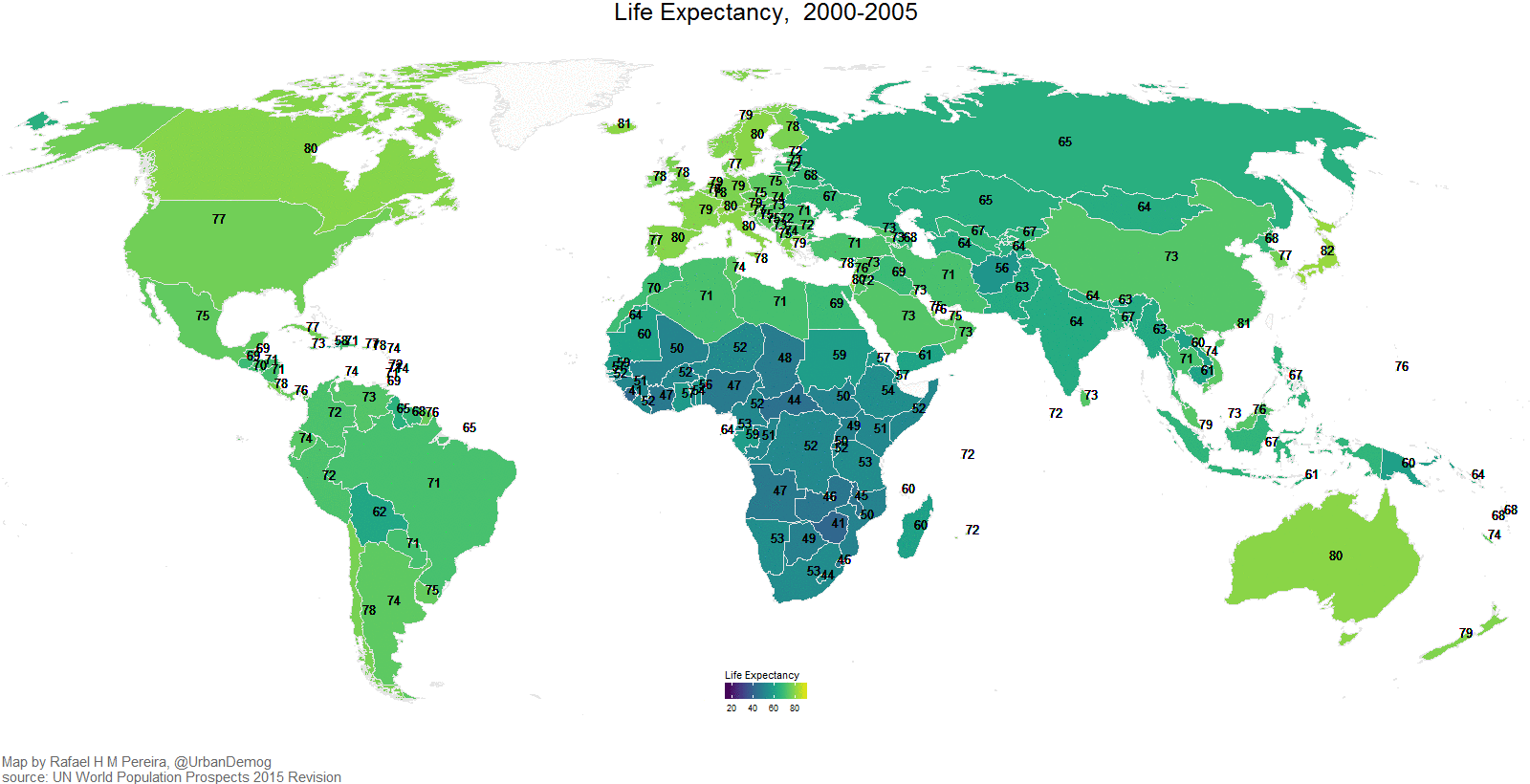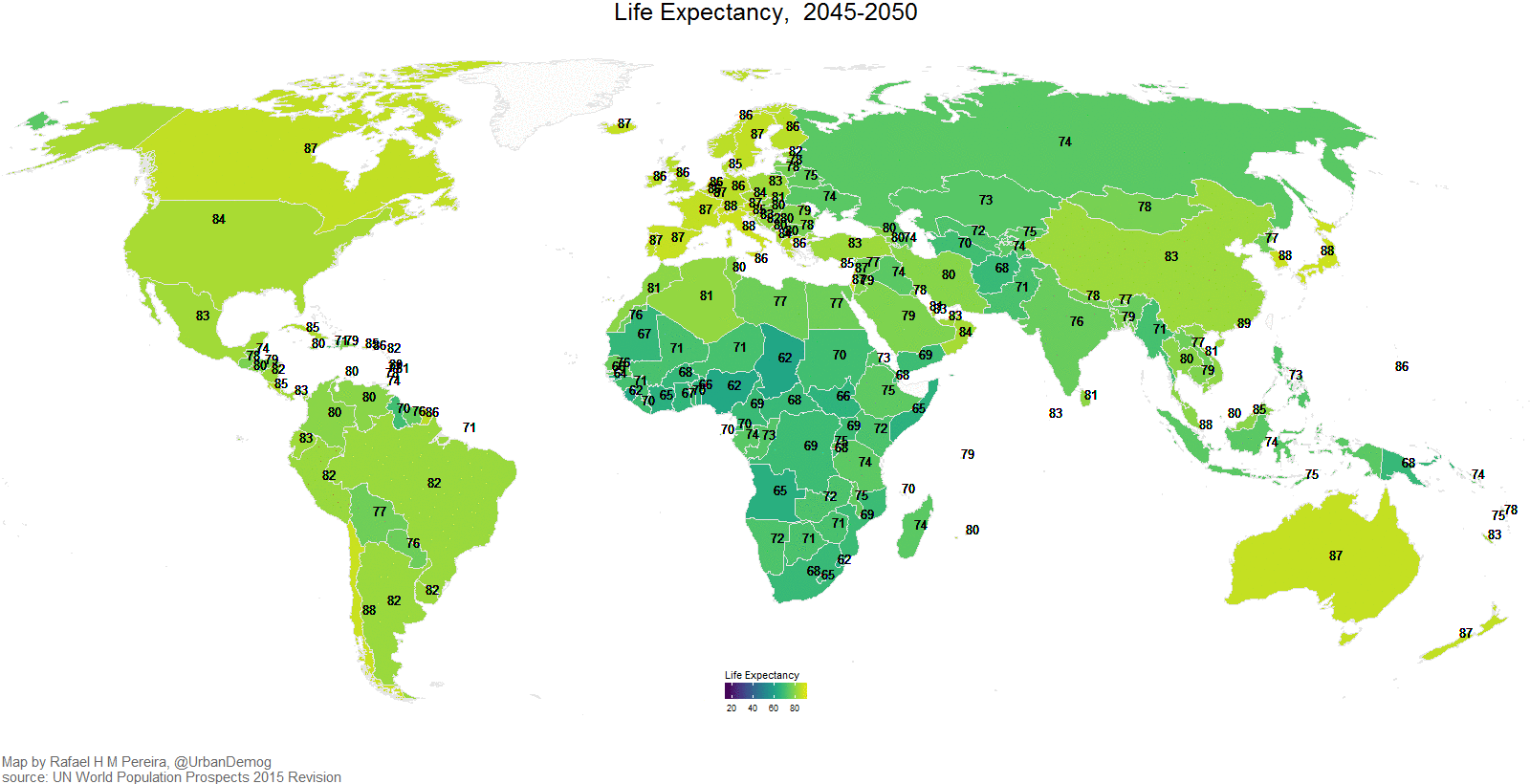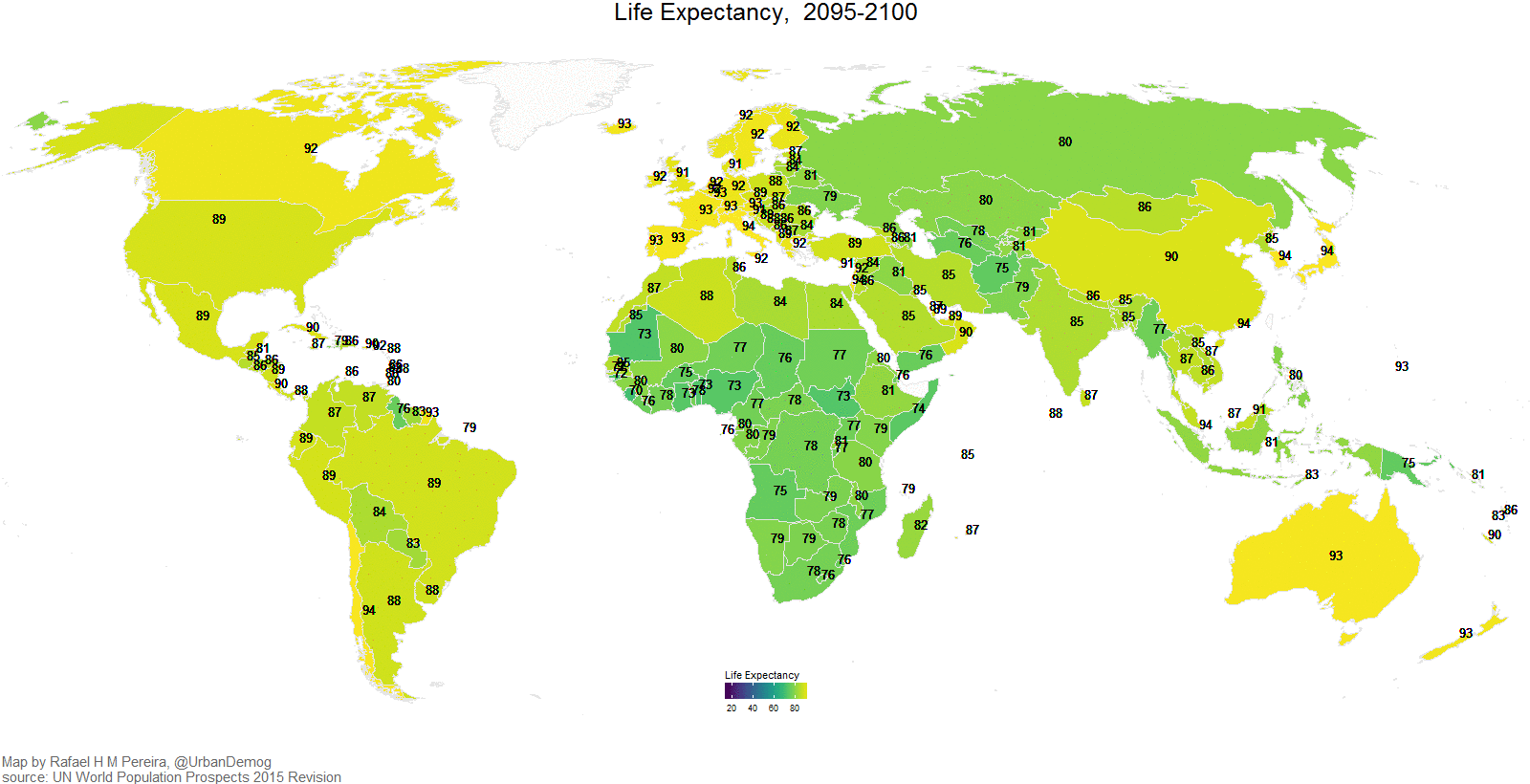
Sasvim je jasno da se, kao što je to slučaj kod pisanog teksta, kartama prenosi neka poruka. One služe da korisnicima odgovore na skup pitanja: Gde…?, Šta…?, Koliko…?, Kakvo…? i Kada…?, (Slike Slika 1.1,Slika 1.2, Slika 1.3, Slika 1.4, Slika 1.5)
Klasifikacija karata
Karte se mogu klasifikovati prema medijima koji se koriste za njihovo prenošenje korisnicima i prema tipovima informacija koje prenose.
Kada govorimo o medijima kojima se karte prenose korisnicima, tri tipa medija koji se koriste u kartografiji su: opipljivi, virtuelni i mentalni.
Opipljiva karta je ona koja se može držati u rukama, kao na primer papirna karta. Dobra stvar u vezi sa ovim kartama je što se mogu lako deliti između korisnika i nije potreban specijalizovan hardver niti softver da bi se koristile. Takođe, opipljive karte su prenosive i mogu se čuvati dugo vremena bez potrebe za održavanjem.
Virtuelna karta ili digitalna karta je bilo koja karta prikazana na elektronskom uređaju. Karte se danas mogu naći na desktop računarima, laptopovima, tabletima, mobilnim telefonima, GPS prijemnicima i raznim drugim digitalnim uređajima. Prednost virtuelnih karata je ta što se one mogu lako ažurirati, dinamične su, prikazuju animaciju, mogu se povezati na velike količine informacija kao što su dokumenti, slike, filmovi i zvuk, i mogu se lako deliti. Negativni aspekti virtuelnih karata su sledeći: gledanje ovih karata zahteva odgovarajući hardver i softver, potrebno ih je održavati, moguće je da ne budu intuitivne za brojne korisnike, i zahtevaju više obuke da bi se izrađivale.
Mentalna karta je ona karta koja se nalazi u nečijem umu i njegovoj specifičnoj konceptualizaciji prostora. Mentalne karte se prenose kroz konverziju u opipljive ili virtuelne karte, ali i putem drugih vrsta komunikacije kao što su govor ili pisanje.
Opipljive i virtuelne karte mogu biti opšte referentne karte ili tematske karte.
Opšte referentne karte naglašavaju lokaciju i prikazuju veliki broj raznih pojava. One primarno prikazuju objekte, njihovu lokaciju i informaciju kojom se oni identifikuju. Opšte referentne karte nisu specijalizovane ni za jednu posebnu primenu, nego su namenjene širokom spektru aktivnosti. Primeri opštih referentni karata su: topografske karte, globalne veb-karte (npr. Google Maps, OpenStreetMap, itd.).
Tematske karte naglašavaju karakteristike koje se odnose na pojedinačne teme. One tipično imaju veoma specifičnu namenu i prenose specifičnu poruku u vezi sa jednom temom koja se uobičajeno povezuje sa nekom karakteristikom (atributom). Tematske karte prikazuju prostorne i vremenske obrasce određene teme. Za razliku od opštih referentnih karata, tematske karte su obično veoma selektivne kada je reč o objektima ili pojavama koje se prikazuju na karti. Tematske karte mogu biti kvalitativne i kvantitativne. Kvalitativne tematske karte prikazuju kvalitativne karakteristike pojave ili pojava koje su u fokusu karte, dok se u slučaju kvantitativnih tematskih karata prikazuju apsolutne i relativne kvantitativne informacije u vezi sa pojavama od interesa.
1.2 Definicija kartografije
Kartografija je naučna disciplina koja se bavi metodama izrade i proizvodnje, kao i načinom korišćenja karata. Ili druga definicija glasi: Kartografija je umetnost i nauka pravljenja karata. Kartografija uključuje proces proizvodnje karte koji se odvija na filozofskim i teorijskim osnovama pravljenja karata. Kartograf je neko ko dizajnira i priprema kartu za distribuciju. Drugim rečima, kartograf je neko ko proučava filozofske i teorijske osnove, tj. pravila pravljenja karata. Ranije se smatralo da samo kartografi čije je obučavanje trajalo više godina prakse da bi stekli potrebne veštine i znanja, mogu da izrađuju karte. U današnje vreme, međutim, kartografija je znatno demokratizovana i sada mnogo različitih grupa izrađuje karte bez angažovanja školovanih kartografa.
Kartografija je retko samostalna profesija. Danas se ona smatra skupom veština i znanja koji je potreban geografima, geodetama, geoinformatičarima i drugima koji žele da izrađuju karte.
„Pravljenje karata je možda najstariji oblik primitivne umetnosti… stara koliko i čovekovi prvi tragovi na zidovima pećina i u pesku“, (Brown 1979).
Najstarija postojeća karta pronađena je na arheološkom nalazištu Catalhoyuk u Anadoliji, datira iz oko 6200. godine pre nove ere. Ova karta (Slika 1.6), oslikana na zidu kuće, prikazuje grad i vulkan u erupciji u pozadini.
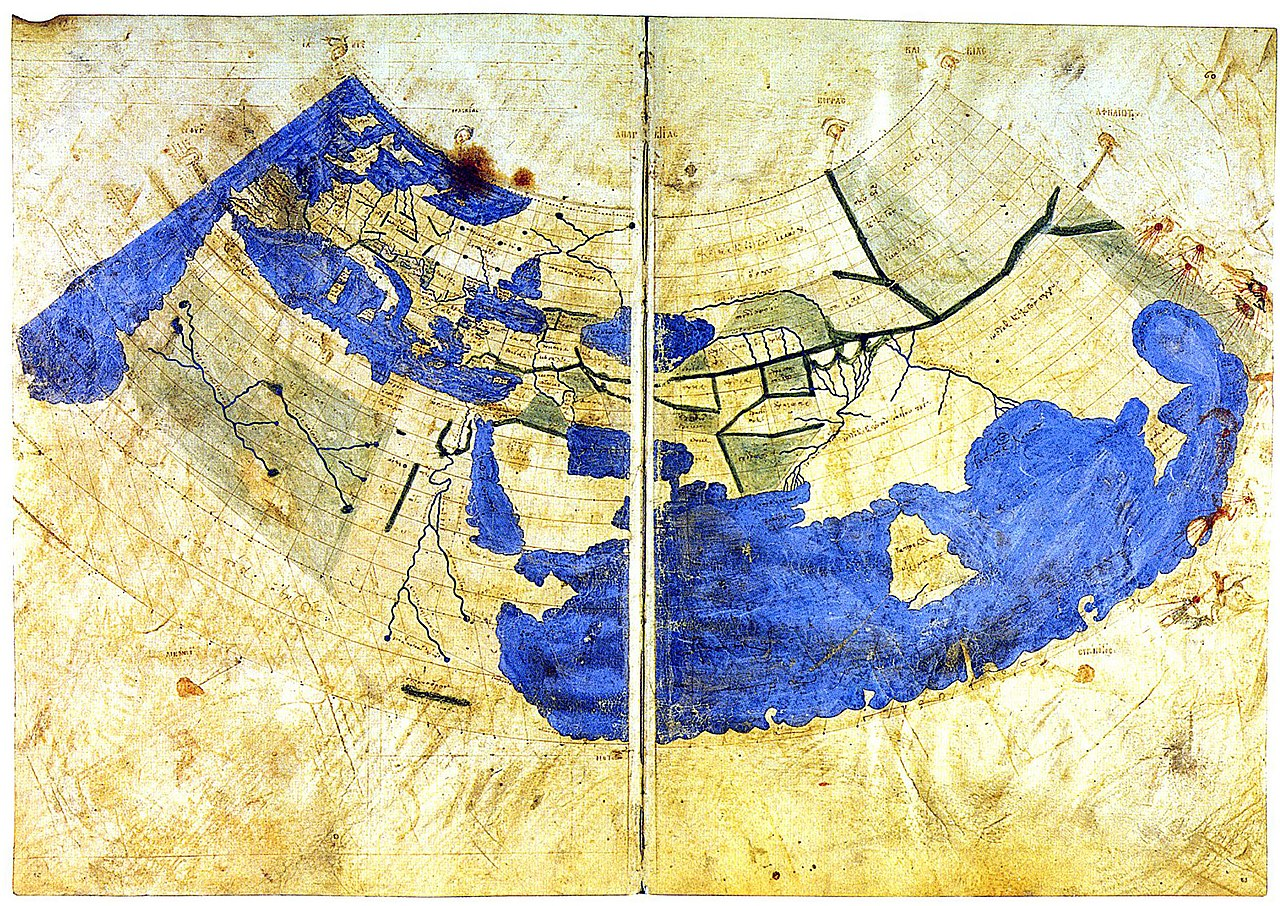
Razvoj matematike i geografije u antičkoj Grčkoj i Rimu doveo je i do razvoja kartografije. Originalne karte iz tog perioda uglavnom nisu sačuvane, ali su sačuvani njihovi srednjevekovni prepisi ili rekonstrukcije, kao što je na primer rekonstrukcija Ptolomejeve karte sveta koju su izradili vizantijski monasi u Konstantinopolju oko 1300. godine (Slika 5.9, Ptolomejeva karta).
U toku srednjeg veka evropska kartografija je bila u ideološkim okvirima hrišćanske religije. Veoma popularne karte tog perioda bile su takozvane „T u O“ karte (Slika 1.8). Na njima je Jerusalim prikazivan u centru, dok je istok orijentisan prema gornjem delu karte. Krug je predstavljao svetski okean, a u njega je bilo upisano slovo T koje je predstavljalo vodene površine koje su ograničavale tada poznate kontinente: Evropu, Aziju i Afriku.
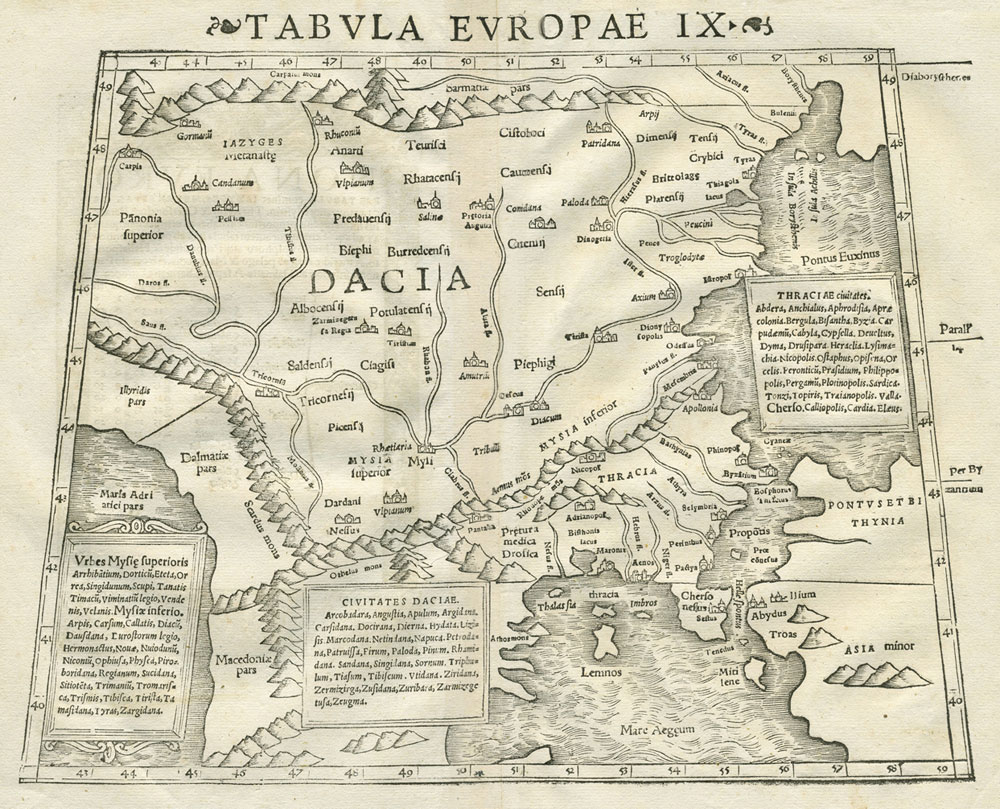
Renesansa je donela dva bitna momenta koji su znatno uticali na razvoj kartografije. Jedan je pronalazak štampe početkom XV veka, što je učinilo karte znatno dostupnijim. Drugi momenat je bio restauracija naučnih znanja iz antike i unapređenje mnogih naučnih disciplina, od kojih su za kartografiju posebno značajne bile geografija, matematika i astronomija. Jedan od najznačajnijih kartografa tog perioda, Sebastian Münster iz Bazela, publikovao je 1540. god. atlas sveta pod nazivom Geographia (Slika 1.9), koji je postao novi globalni standard za karte sveta.
Vidljivi napredak u kartografiji bio je rezultat Velikih otkrića u XV i XVI veku: otkrivena je Amerika, pomorski put za Indiju, počela je kolonizacija drugih kontinenata. Karte su pravljene tako da olakšaju navigaciju na moru pa je fokus bio na kartiranju obalskih linija, ostrva, reka, luka i pojava od interesa za plovidbu. Počeli su da se izrađuju globusi i da se razvijaju nove kartografske projekcije. Za ovo poslednje posebno je zaslužan veliki renesansni kartograf, Flamanac Gerardus Mercator. On je razvio cilindričnu konformnu projekciju za kartu sveta koja je znatno olakšavala navigaciju, (Slika 1.10). Ova projekcija je i danas popularna za prikazivanje globalnih karata.
Doba prosvetiteljstva, koje počinje u drugoj polovini XVII veka, postavlja razum kao primarni izvor autoriteta. Društva intenzivno počinju da baziraju svoja funkcionisanja na znanju i naučnim metodama, a ne na religijskim dogmama. U ovakvom duhu vremena, karte dobijaju ulogu jednog od glavnih prenosioca znanja. Posebno je značajno što se vlade i administrativne institucije sve više oslanjaju na karte da bi regulisale i kontrolisale svoje teritorije. Jedan od najznačajnijih momenata u istoriji kartografije je početak izrade topografske karte Francuske 1670-ih godina, po zahtevu kralja Luja XIV, koju su vodili Giovanni Domenico Cassini i njegovi naslednici. To su bile prve karte čija se izrada zasnivala na geodetskoj triangulaciji, (Slika 1.11).
Može se reći da, kao što se prosvetiteljstvo smatra početkom modernog doba u istoriji, ono je takođe i početak moderne kartografije.
1.3 Kartografski izvori
Da bi se napravila karta ili kartografski proizvodi neophodni su prostorni podaci. Podaci u digitalnoj kartografiji dostupni su iz različitih izvora. Oni često postoje u standardnim GIS formatima i mogu se direktno preuzeti putem veb-servisa. Takođe, mogu se generisati iz geodetskog premera, fotogrametrijskog premera, laserskog skeniranja, daljinske detekcije ili se mogu dobiti koristeći GIS tehnike i tabelarne podatke, npr. podatke o popisu po opštinama i prostorne podatke koji predstavljaju granice opština, moguće ih je spojiti i dobiti prostorne podatke o popisu. Digitalni kartografski podaci se mogu dobiti i digitalizacijom postojećih karata, uključujući i skenirane planove i karte ili procesom kartografske generalizacije. Naizgled neprostorni podaci mogu biti potencijalni kartografski izvor. Podaci o broju učenika po školama u Beogradu mogu postati prostorni podaci, ako za svaku školu imamo adresu, a na osnovu adrese procesom geokodiranja dobijemo koordinate.
Kartografski izvori se mogu slikovito predstaviti na sledećeoj slici (Slika 1.12).
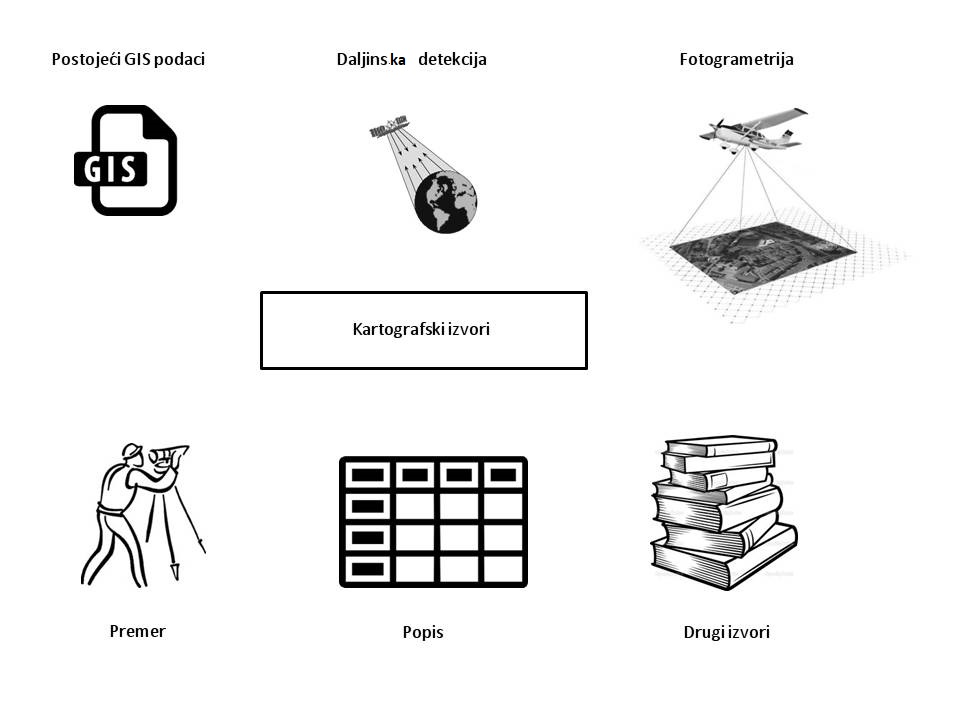
Sve pomenute tehnike prikupljanja prostornih podataka izvode se sa ciljem da deo realnog sveta (npr. neki prirodni fenomen u prostoru) bude opisan prostornim podacima koji uglavnom sadrže podatke o lokaciji u prostoru (najćešće koordinate) pridružene nekim atributima. Atribut može biti dobijen direktno iz nekog senzora ili se može pridružiti na osnovu zapažanja onog ko prikuplja podatke. Na primer, kad imamo meteorološku stanicu, onda je uobičajeno da imamo lokaciju te stanice zajedno sa merenjima klimatskih promenljivih i vremenom opažanja. U ovom slučaju to su prostorno vremenski podaci, gde se pored lokacije beleži i vreme opažanja nekog fenomena. U opštem slučaju, da bismo modelirali geografsku realnost, neophodni su nam što kvalitetniji prostorno vremenski podaci.
Kod primera meteorološke stanice opažanja sa senzora su najčešće numerički podaci kao što je vrednost temperature, količina padavina i slično, ali u istom primeru često se prikupljaju i kategorijski podaci kao na primer da li je maglovito ili ne, da li je vedro ili oblačno i sl. Dakle, najčešće prostorne fenomene opisujemo dvema vrstama podataka: kvantitativni (numerički) i kvalitativni (opisni). Ako su opisni podaci svrstani u klase, kategorije (npr. oblačnost može biti iskazana u 3 klase: vedro, umereno oblačno i potpuno oblačno), onda su to kategorijski ili faktorski podaci.
Podaci koji se odnose na diskretan broj opažanja u prostoru nazivaju se vektorski podaci. Vektorski podaci imaju osobinu da se njima opisuju fenomeni čije se prostorno prostiranje apstrahuje tačkom, linijom ili poligonom u prostoru. Ako posmatramo mrežu meteoroloških stanica ona predstavlja vektorski sloj podataka, (Slika 1.13 u Robinsonovoj projekciji), gde svaka stanica iz mreže predstavlja entitet iz vektorskog sloja.
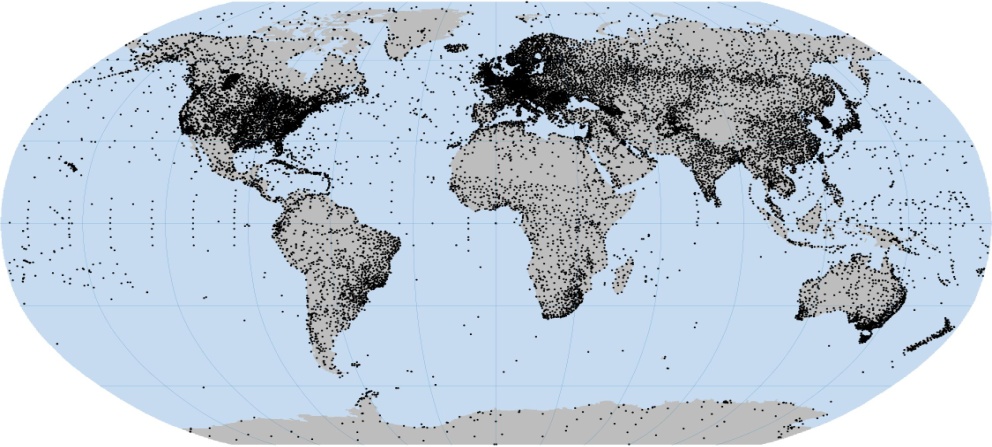
Na osnovu gore prikazanog seta podataka o temperaturama možemo imati informaciju o temperaturi na lokaciji svake meteorološke stanice, ali nam nije poznata vrednost temperature na lokacijama na kojim nije bilo opažanja. Ako posmatramo temperaturno polje, skup svih temperatura u datom momentu, na svakoj lokaciji, onda za prikaz takvog polja koristimo prostornu strukturu pravilnog grida ili rastera. Kontinualni podaci vrednosti temperature na pravilnom gridu 1x1 km prikazani su na slici, (Slika 1.14). Takav pravilan grid predstavlja rasterski podatak, o kojem će kasnije biti više reči.
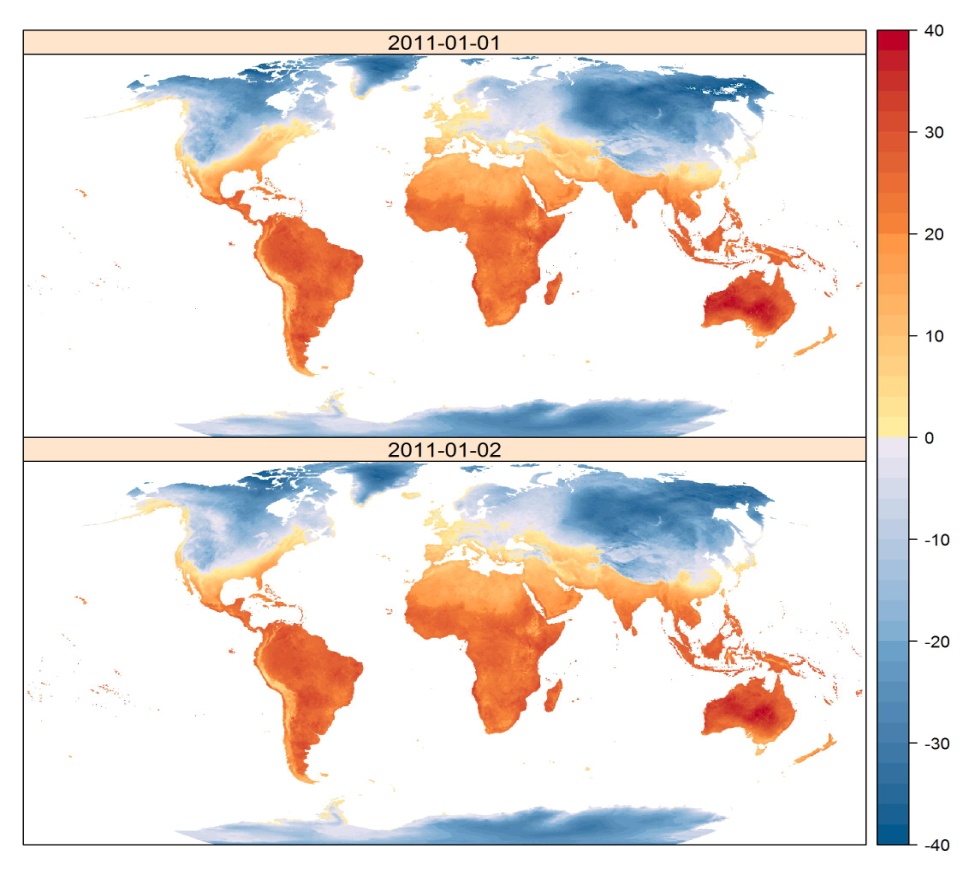
Raster ili grid je prostorna struktura podataka koja deli prostor u pravougaone ćelije (piksele) koje sadrže jednu ili više vrednosti nekog opažanog ili modeliranog fenomena. Analogija sa atributima kod vektorskih podataka je jasna, vrednosti ćelija su uglavnom numerički ili kategorijski podaci. Često rasterske podatke dobijamo i na osnovu fotogrametrijskog premera, kao proizvod daljinske detekcije, tj. to su optički ili radarski snimci, snimci temperature tla, itd.
1.4 Vektorski podaci
Vektorski podaci predstavljaju strukturu podataka u GIS-u gde se geometrija i pozicija čuvaju kao parovi (\(x,y\)) koordinata. Pored koordinata čuvaju se i informacije o koordinatnom referentnom sistemu, biće više reči o tome u sledećem poglavlju. Kod tačkastih podataka, pored geometrije za svaku tačku, uobičajeno je da se čuvaju i atributni podaci. Takvi podaci se mogu predstaviti i običnom tabelom podataka, u kojoj se čuvaju podaci o lokaciji i atributni podaci.
| Geometrija | Atribut 1 | Atribut 2 | Atribut 3 |
|---|---|---|---|
| (x1 y1) | Vrednost 1 | Vrednost 2 | Vrednost 3 |
| (x2 y2) | Vrednost 4 | Vrednost 5 | Vrednost 6 |
Kod llinijskih podataka linija je predstavljena setom koordinatnih parova, koji su spojeni od tačke do tačke redom, linijskim segmentima, kao što bi se spojilo olovkom vodeći računa o redosledu (primeri: putevi, dalekovod, metro linija itd.). Poligoni su organizovani slično kao linije koje počinju i završavaju se u istoj tački (primeri: adminstrativne jedinice, granice opština, jezero, šuma itd.). Redosled iscrtavanja linija (segmenata) kod poligona najčešće je definisan suprotno pravcu kretanja kazaljke na satu za obuhvaćenu površinu, dok se za praznine unutar površine koristi pravac kretanja kazaljke na satu, ili obrnuto, zavisno od formata podataka. Primer vektorskih geometrijskih primitiva u Well Known Text formatu dat je u tabeli, (Tabela 1.2). Kako kod vektorskih, tako i kod rasterskih podataka postoji veliki broj formata koji su se koristili i koji se danas koriste za čuvanje prostornih podataka. Istoriju razvoja formata i sistema za manipulaciju prostornim podacima veoma slikovito opisali su Pebesma i koautori (http://r-spatial.org/2016/11/29/openeo.html).
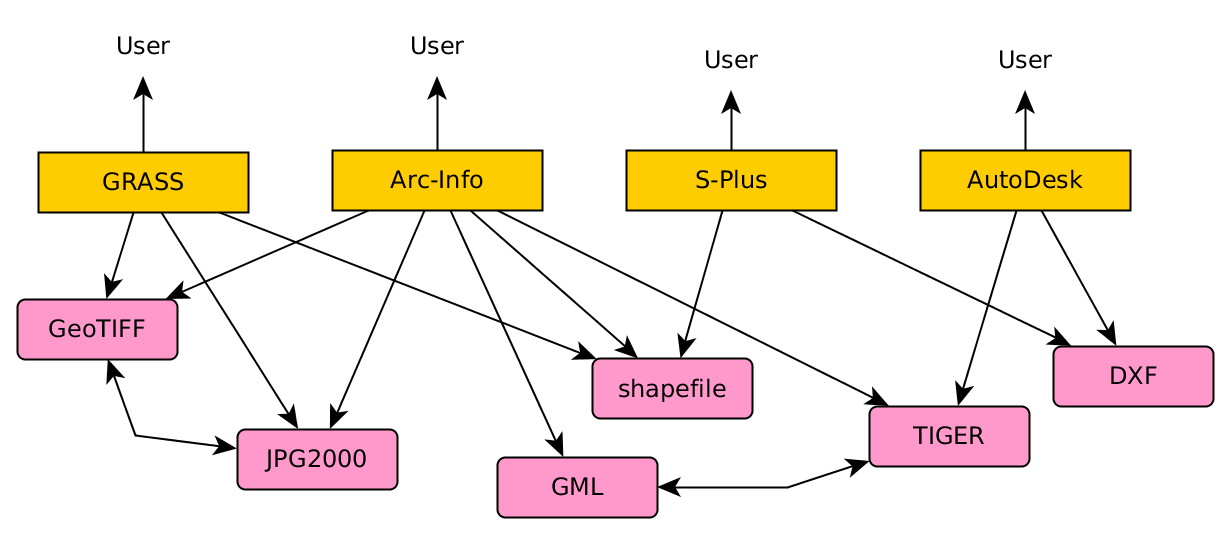
Osamdesetih godina prošlog veka praktično svaki proizvođač softvera je imao svoj način čuvanja prostornih podataka, Slika 1.15, Pebesma et al. (2016).
Devedesetih godina prošlog veka došlo je do promene. Više proizvođača softvera počelo je da koristi nekoliko formata za prostorne podatke. Zbog toga je bilo moguće koristiti isti format u različitim GIS okruženjima, nekad uz neophodnu konverziju, ali interoperabilnost je bila moguća, Slika 1.16, Pebesma et al. (2016).
| Tip | Primer koristeći Well Known Text sintaksu | WKT |
|---|---|---|
| Tačka |  |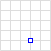
POINT (30 10) |
| Linija |  |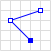
LINESTRING (30 10, 10 30, 40 40) |
| Poligon |  |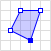
POLYGON ((30 10, 40 40, 20 40, 10 20, 30 10)) |
| Poligon sa prazninom |  |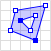
POLYGON ((35 10, 45 45, 15 40, 10 20, 35 10), (20 30, 35 35, 30 20, 20 30)) |
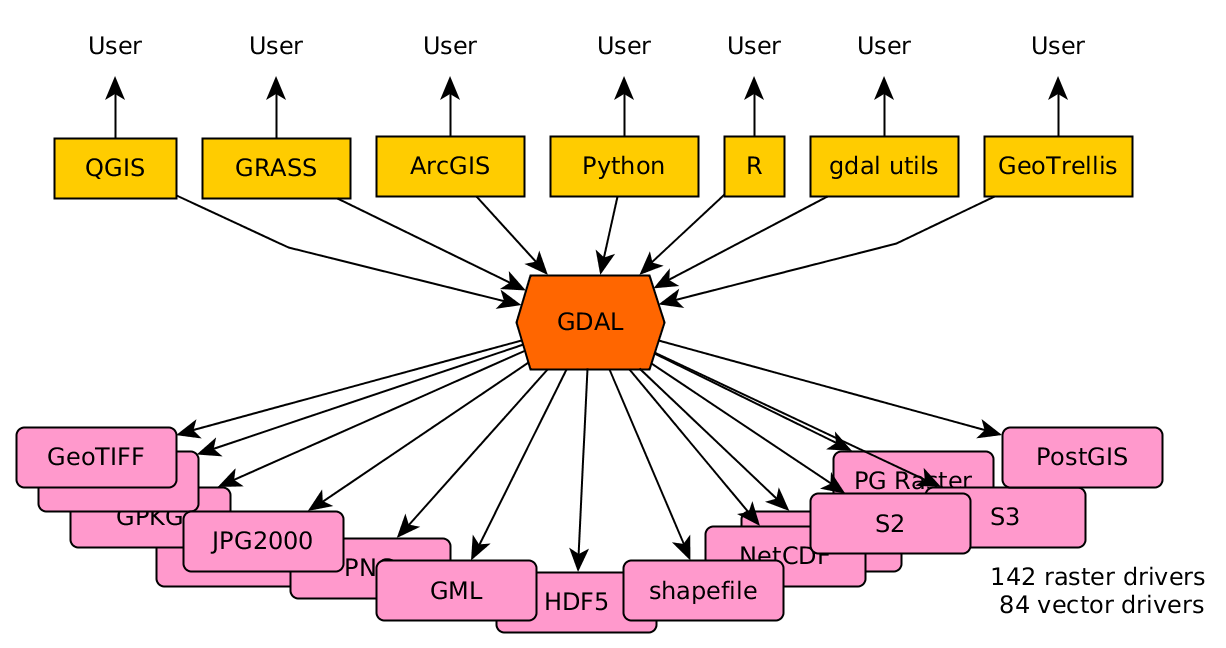
Nakon toga, 2000. godine napravljena je GDAL(Geospatial Data Abstraction Layer http://www.gdal.org/) biblioteka otvorenog koda (eng. open source). GDAL biblioteka omogućava čitanje i pisanje različitih formata, kako vektorskih, tako i rasterskih struktura podataka. Praktično je napravljena jedna biblioteka za konverziju i omogućila je korišćenje različitih tipova podataka u skoro svim GIS sistemima, Slika 1.17, (Pebesma et al. 2016).
Postoje razni formati za prostorne podatke u vektorskom obliku kao što su: GeoPackage-gpkg, ESRI Shapefile-shp, Geographic Markup Language-GML, KML, GeoJSON i drugi, videti detaljnije u knjizi (Kilibarda and Protić 2018). Well Known Text - WKT je markup jezik za reprezentaciju prostornih vektorskih podataka koji se vrlo često primenjuje kod prostornih baza podataka, tako da je pogodan kod tabelarnog prikaza podataka. U tabeli (Tabela 1.3) dat jednostavan primer sa samo jednim vektorskim entitetom. WKT podržava osnovne geometrijske primitive: tačke, linije, poligone i više tačaka (kao jedan entitet), više linija (kao jedan entitet), više poligona (kao jedan entitet) i geometrijsku kolekciju (kao jedan entitet).
| WKT_WGS84 | id | Naziv | url |
|---|---|---|---|
| POINT (20.476164 44.805681) | 1 | Građevinski fakultet | www.grf.rs |
Generalno, multi geometrijski primitivi su prikazani slikovito na sledećoj slici (Slika 1.18).
Primeri WKT geometrije:
POINT (21 45)
MULTIPOINT ((21 45), (22 46), (22.4 46), (22 46.3), (21 46.4))
LINESTRING (21 45, 21.5 45, 21.5 46, 21.5 46.3, 21.6 46.5, 22 46.83)
MULTILINESTRING ((21 45, 21.5 45, 22.5 46, 24 46, 23 44, 22 43),
(23 50, 23.3 55, 25 56))
POLYGON ((22 45, 23 45, 5 22, 6 3, 22.5 3, 24.2 46.2, 25.2 47.2, 25.5 47.3, 22 45),
(22 46, 23.3 46.6, 4 3, 4 46, 22 45))
MULTIPOLYGON (((22 45, 22.3 45, 22.5 46, 22.6 46.3, 22.7 46.4, 24.2 46.2, 25.2 47.2, 21 47.3, 22 45),
(22 46, 23.3 46.6, 23.4 46.7, 24 46.9, 22 46)), ((23 47, 23.4 47, 23.5 47.8, 23 47.9, 23.9 47.8, 23 47)))
GEOMETRYCOLLECTION (
POLYGON ((22 45, 23 45, 25 46, 26 46.3, 22.5 47.3, 24.2 46.2, 25.2 47.2, 45 3, 22 45),
(22 46 , 23.3 46.6, 24 46.3, 24 46.8, 22 46)),
LINESTRING (21 46, 22.5 46.1, 22.5 46.11, 24 46, 25.3 46.9, 25.2 47),
POINT (22 44.5),
POINT (25 44)
)Na slici (Slika 1.19) dat je primer globalne karte očekivanog životnog veka po državama koristeći podatke sadržane u paketu spData (Bivand, Nowosad, and Lovelace 2022). Metodom st_transform vrši se transformacija iz jednog koordinatnog referentnog sistema u drugi, ovaj metod se koristi ako se manipuliše objektima iz klasa paketa sf. Ovde su podaci transformisani u Molvajdovu pseudocilindričnu ekvivalentnu projekciju. Metod plot se odnosi i na sf objekte. Ovim metodom lako se dodaju neki elementi karte, kao na primer koordinatna mreža, koja se dodaje koristeći argument graticule = TRUE, Slika 1.19.
Code
library(sf)
# Warning: package 'sf' was built under R version 4.2.3
library(spData)
# Warning: package 'spData' was built under R version 4.2.3
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
world_mollweide = st_transform(world, crs = "+proj=moll")
plot(world_mollweide["lifeExp"], graticule = TRUE,
main = "Očekivani životni vek za rođene 2014.")
Code
# https://geopandas.org/en/stable/docs/user_guide/mapping.html
import geopandas as gpd
import matplotlib.pyplot as plt
# podaci su data folderu u radnom direktodijumu
# preuzeti sa linka
# https://github.com/Nowosad/spData/blob/master/inst/shapes/world.gpkg
gdf = gpd.read_file("data/world.gpkg")
gdf_moll = gdf.to_crs("+proj=moll")
# podaci preuzeti sa
# https://github.com/nvkelso/natural-earth-vector/tree/master/updates/version_1d4/110m_physical/ne_110m_graticules_all
graticules = gpd.read_file("data/negrat/ne_110m_graticules_10.shp")
graticules_moll=graticules.to_crs("+proj=moll")
fig, ax = plt.subplots(1, 1)
graticules_moll.plot(ax=ax, color='lightgray', linewidth=0.5)
plt.title("Očekivani životni vek za rođene 2014.")
gdf_moll.plot(column="lifeExp" , ax=ax, legend=True)
Kratak opis podataka je sledeći: svaka država je predstavljena koristeći geometrijski primitiv više poligona (kao jedan entitet multipoligon, npr. Srbija se može predstaviti jednim poligonom, ali Grčka ima više od 1.000 ostrva tako da je neophodno predstaviti je entitetom koji sadrži više poligona), ima ukupno 177 vektorskih entiteta u ovom setu podataka, svaki entitet ima 10 atributa, među njima je i lifeExp, očekivani životni vek. Dat je koordinatni referentni sistem sa projekcijom u kojoj su podaci, prostorni obuhvat i drugo.
world_mollweide
# Simple feature collection with 176 features and 10 fields
# Geometry type: GEOMETRY
# Dimension: XY
# Bounding box: xmin: -17600000 ymin: -9020000 xmax: 17600000 ymax: 8750000
# Projected CRS: +proj=moll
# # A tibble: 176 × 11
# iso_a2 name_long continent region_un subregion type area_km2
# * <chr> <chr> <chr> <chr> <chr> <chr> <dbl>
# 1 FJ Fiji Oceania Oceania Melanesia Sove… 1.93e4
# 2 TZ Tanzania Africa Africa Eastern … Sove… 9.33e5
# 3 EH Western Sahara Africa Africa Northern… Inde… 9.63e4
# 4 CA Canada North Am… Americas Northern… Sove… 1.00e7
# 5 US United States North Am… Americas Northern… Coun… 9.51e6
# 6 KZ Kazakhstan Asia Asia Central … Sove… 2.73e6
# # ℹ 170 more rows
# # ℹ 4 more variables: pop <dbl>, lifeExp <dbl>, gdpPercap <dbl>,
# # geom <MULTIPOLYGON [m]>
gdf_moll
# iso_a2 ... geometry
# 0 FJ ... MULTIPOLYGON (((-17574510.593 -2036027.390, -1...
# 1 TZ ... MULTIPOLYGON (((3397635.186 -117460.561, 31933...
# 2 EH ... MULTIPOLYGON (((-805662.249 3368332.366, -8198...
# 3 CA ... MULTIPOLYGON (((-9533466.708 6289750.807, -954...
# 4 US ... MULTIPOLYGON (((-10290289.313 7230369.657, -10...
# .. ... ... ...
# 171 MK ... MULTIPOLYGON (((1859040.057 5047061.381, 18208...
# 172 RS ... POLYGON ((1718202.506 4995715.165, 1728946.159...
# 173 ME ... MULTIPOLYGON (((1662701.827 5076640.651, 16743...
# 174 TT ... MULTIPOLYGON (((-6114434.039 1327419.380, -611...
# 175 SS ... MULTIPOLYGON (((3086677.985 433787.108, 312730...
#
# [176 rows x 11 columns]Izvori dostupnih vektorskih podataka
U ovom poglavlju kratko će biti pomenuti neki izvori vektorskih podataka, odakle se mogu preuzeti besplatni vektorski podaci (otvoreni podaci).
Open Data Institute definiše otvorene podatke na sledeći način:
- podaci koji se lako dele putem Interneta,
- dostupni su u standardnom formatu,
- imaju garantovanu dostupnost i konzistenciju u vremenu,
- imaju jasan opis kako su nastali.
Natural Earth ‒ Portal za preuzimanje vektorskih i rasterskih podataka različitog nivoa detaljnosti i tačnosti, podaci su besplatni. Url adresa: http://www.naturalearthdata.com.
Esri Open Data ‒ Kompanija Esri je 2017 napravila geoportal za preuzimanje velikog broja GIS setova podataka kako vektorskih tako i rasterskih u standardnim GIS foramatima. Url adresa: https://hub.arcgis.com/pages/open-data.
OpenStreetMap (OSM) ‒ je najveća volonterska baza i veb-portal prostornih podataka slična komercijalnim portalima kao što su Google Maps ili Bing Maps, ali s tom razlikom da je moguće preuzeti vektorske podatke u formatu koji obezbeđuje OpenStreetMap organizacija. Za konverziju u standardne formate može se koristiti neki od QGIS dodataka (plugin) za preuzimanje OSM podataka. Url adresa: https://www.openstreetmap.org/.
GADM je baza podataka o administrativnim granicama organizovana u više hijerarhijskih nivoa i dostupna je u standardnim GIS formatima. Url adresa: http://gadm.org/.
GeoNames je baza geografskih naziva, toponima, sa lokacijom naziva i dodatnim atributima, podaci se mogu preuzeti u tekstualnom formatu, ali se lako mogu konvertovati u neki od GIS vektorskih formata. Url adresa: http://www.geonames.org.
Na url adresi https://freegisdata.rtwilson.com/ može se naći lista velikog broja izvora, kako vektorskih, tako i rasterskih podataka, grupisanih po kategorijama.
1.5 Rasterski podaci
Kao što je rečeno u uvodnom poglavlju Sekcija 1.3, raster ili grid je prostorna struktura podataka koja deli prostor u pravougaone ćelije (piksele) koje sadrže jednu ili više vrednosti nekog opažanog ili modeliranog fenomena, vrednosti ćelija su uglavnom numerički ili kategorijski podaci.
Raster (grid) koji ima jednu atributnu vrednost podseća na matricu koja dodatno ima definisano i zaglavlje. Postavlja se pitanje kako se definiše georeferencija kod rasterskih podataka. Praktično ona je sadržana u zaglavlju. Zavisno od formata rasterskih podataka, u zaglavlju se najčešće nalaze podaci o koordinatnom referentnom sistemu (kod nekih formata su u zasebnom fajlu), broju vrsta i kolona matrice podataka, koordinatama početne ćelije (piksela), veličini piksela (neki formati podržavaju samo kvadratne dok drugi podržavaju i pravougaone piksele), informacija kako je zapisana vrednost za piksele koji nemaju atributnu vrednost. Slika 1.20 prikazuje primer rastera, prikazan je digitalni model visina (DEM) za područje Krupnja i okoline u Srbiji, raster je u Gaus-Krigerovoj projekciji 7 zona, perspektivni prikaz dat je na slici (Slika 1.21).
Koristeći GDAL funkciju gdalinfo, mogu se dobiti informacije o prikazanom rasteru, Slika 1.20.
gdalinfo DEM.asc
Files: DEM.asc
DEM.prj
Size is 397, 334
Coordinate System is:
PROJCS["unnamed",
GEOGCS[,
DATUM["unknown",
SPHEROID["bessel",6377397.155,299.1528128]],
PRIMEM["Greenwich",0],
UNIT["degree",0.0174532925199433]],
PROJECTION["Transverse_Mercator"],
PARAMETER["latitude_of_origin",0],
PARAMETER["central_meridian",21],
PARAMETER["scale_factor",0.9999],
PARAMETER["false_easting",7500000],
PARAMETER["false_northing",0],
UNIT["metre",1,AUTHORITY["EPSG","9001"]]]
Origin = (7354715.404513620771468,4930131.364209158346057)
Pixel Size = (90.000000000000000,-90.000000000000000)
Corner Coordinates:
Upper Left ( 7354715.405, 4930131.364) ( 19d10' 4.27"E, 44d29'47.38"N)
Lower Left ( 7354715.405, 4900071.364) ( 19d10'34.54"E, 44d13'33.90"N)
Upper Right ( 7390445.405, 4930131.364) ( 19d37' 1.14"E, 44d30'10.14"N)
Lower Right ( 7390445.405, 4900071.364) ( 19d37'24.00"E, 44d13'56.45"N)
Center ( 7372580.405, 4915101.364) ( 19d23'45.97"E, 44d21'52.76"N)
Band 1 Block=397x1 Type=Float32, ColorInterp=Undefined
NoData Value=-32767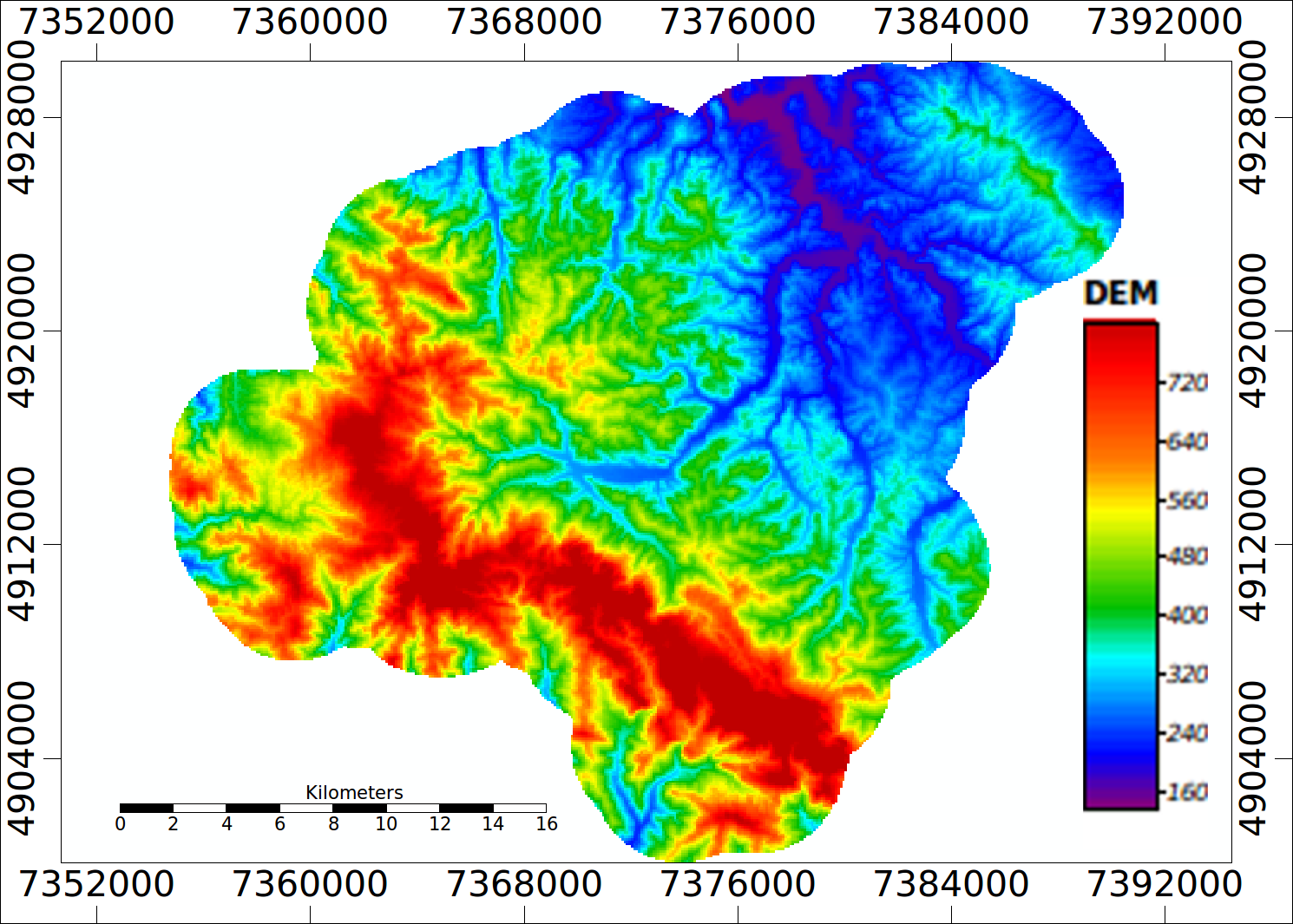
Koordinate bilo kog piksela u rasteru mogu se dobiti ako se poznaju koordinate početnog piksela, Slika 1.22 to objašnjava.
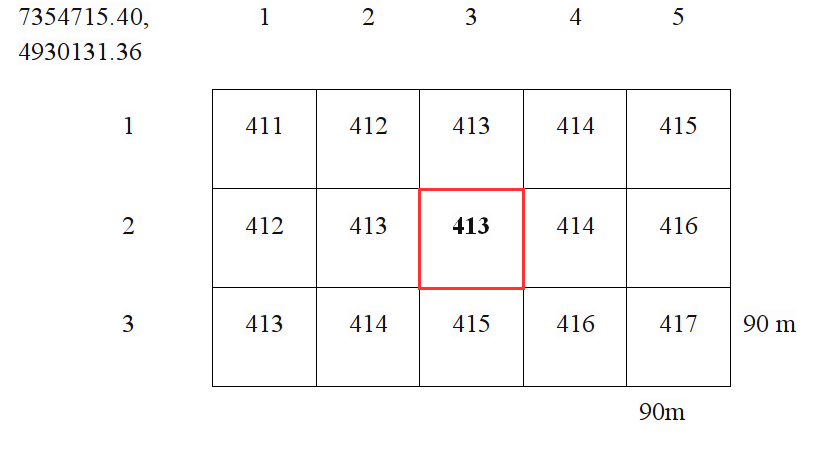
7354715.40 + 3x90 i 4930131.36 - 2x90.Često je raster višedimenzionalan, tj. ima više od jednog atributa, onda je ta struktura slična višedimenzionalnim matricama, često se rasterski atributi kolokvijalno nazivaju kanali (eng. bands), Slika 1.23.
Najpopularniji rasterski formati su: GeoTIFF sa ekstenzijom .tif, ESRI Ascii - .asc, SAGA GIS - .sdat, IDRISI IDRISI - .rst, netCDF i drugi. Lista rasterskih formata koje podržava GDAL biblioteka sa opisom formata dostupna je na url adresi http://www.gdal.org/formats_list.html. Koristeći GDAL biblioteku lako je transformisati rasterske formate iz jednog u drugi format.
Sledeći kod konvertuje ESRI Ascii format u GeoTIFF format koristeći GDAL funkciju gdal_translat.
gdal_translate -of GTiff DEM.asc DEM.tif Oznaka -of predstavlja argument funkcije kojom se zadaje izlazni format, potom slede ulazni i izlazni fajl razdvojeni razmakom. Detaljan opis funkcije dostupan je na url adresi: http://www.gdal.org/gdal_translate.html.
Slobodno dostupni rasterski podaci
U ovom poglavlju su kratko opisani neki od najznačajnih izvora slobodno dostupnih rasterskih podataka:
USGS Earth Explorer, geoportal za pregled i preuzimanje podataka, koji sadrži više izvora rasterskih podataka:
Digitalne modele terena iz misija ASTER (DEM 30 m rezolucije u GeoTIFF formatu) i Shuttle Radar Topography Missions (DEM 90 m rezolucije u GeoTIFF formatu),
Landsat multispektralne satelitske snimke sa istorijskim podacima 40 godina unazad,
Url adresa http://earthexplorer.usgs.gov/.
Sentinels Scientific Data Hub je oficijelni portal podataka za distribuciju satelitskih snimaka od strane Evropske svemirske agencije (European Space Agency ‒ ESA), koji obezbeđuje Sentinel satelitske snimke:
- Sentinel-2a i 2b multispektralne optičke snimke sa 10 m prostornom rezolucijom za vidljivi deo spektra i blisko infracrveni kanal, sa ukupno 12 kanala i prostornom rezolucijom za ostale kanale od 20 m i 60 m.
- Sentinel-1 radarske snimke.
Url adresa: https://scihub.copernicus.eu/dhus. (Copernicus Land Monitoring Service, https://land.copernicus.eu )
Global Land Cover Facility (GLCF) sadrži globalne podatke o zemljišnom pokrivaču koji su nastali na bazi Landsat, MODIS i AVHRR satelitskih misija. Podaci uključuju vegetaciju, vodene površine, geologiju, poljoprivredu i urbana područja. Pored pomenutih podataka ovaj portal obezbeđuje i dodatne podatke kao što su DEM i druge.
Url adresa: http://landcover.org/.
OpenLandMap je geoportal koji nudi slobodno dostupne rasterske podatke iz više tematskih celina uključujući: podatke o reljefu, zemljištu, vegetacione indekse, klimatkse podatke itd.
Url adresa: https://openlandmap.org/
SoilGrids je geoportal za rasterski set podataka o osobinama zemljišta koji sadrži numeričke i faktorske podatke u prostornoj rezoluciji 1 km i 250 m, podaci su dostupni u GeoTIFF formatu.
Url adresa: https://soilgrids.org/.
Uobičajeno je da se kartografski proizvodi prave koristeći i rasterske i vektorske podatke zajedno. Primer kompozicije digitalne karte u QGIS softveru je dat na slici (Slika 1.24).
1.6 Podela kartografije
Kartografija se deli na:
opštu kartografiju,
tematsku kartografiju,
praktičnu kartografiju,
veb kartografiju,
tzv. metakartografiju i
matematičku kartografiju ili kartografske projekcije.
Opšta kartografija ‒ izučava osnovna svojstva geografskih karata, elemente sadržaja i načine njegovog prikazivanja (ključ kartografskih znakova, itd.). Razrađuje i izučava i druge probleme od opšteg značaja za izradu karata (kartografsko generalisanje, primena automatizacije u kartografiji, itd.). U ovom delu takode se izučava istorija razvoja karata i kartografije uopšte.
Tematska kartografija ‒ izučava principe izrade tematskih karata, obrađuje specifičnosti prikaza tematskog sadržaja karte i iznalaženje najboljeg odnosa izmedu ovog i ostalog sadržaja (opštegeografske osnove). Primer tematske karte dat je na slici, (Slika 1.25).
Praktična kartografija ‒ izučava probleme u vezi sa kreiranjem i oblikovanjem sadržaja karata: izradu i sastavljanje karata iz podataka dobijenih na osnovu fotogrametrijskog i topografskog premera, kao i kreiranje raznovrsnih opštegeografskih karata na osnovu postojećih (gotovih) karata. U okviru praktične kartografije posebnu celinu čini oblast reprodukcije (umnožavanja) karata. Primer dela karte koju izrađuje Vojno geografski institut u Beogradu.
Veb kartografija ‒ Veb-kartografija predstavlja granu kartografije koja izučava: tehnike dizajniranja i implementacije karata na veb-u, načine korišćenja veb-karata i sl. U užem smislu veb-kartografija izučava tehnologije dizajniranja, implementacije i diseminacije karata na veb-u.
Primeri veb-kartografskih aplikacija:
Primer veb kartografske aplikacije dat je na slici (Slika 1.27).
Metakartografija ‒ razmatra opšte izražajne mogućnosti karte i kartografskog prikaza.
Matematička kartografija ‒ bavi se izučavanjem tzv. matematičke osnove karte koju čine:
- koordinatni sistem,
- geodetska osnova,
- kartografska projekcija i razmer.
U ovom delu najviše prostora posvećuje se teoriji kartografskih projekcija (preslikavanja), odnosno načinima računanja koordinata. Isto tako izučavaju se načini korišćenja geodetske osnove u procesu izrade karata, kao i metodi svođenja kartografskih materijala u jedinstven sistem koordinata (koordinatne transformacije). Prikaz planete u streografskoj projekciji dat je na slici (Slika 1.28).
1.7 Zadaci matematičke kartografije
U ovom delu će biti opisani zadaci matematičke kartografije, ali, da bismo razumeli zadatke, neophodno je da se kratko osvrnemo na aproksimaciju planete Zemlje. Matematička kartografija se bavi matematičkim funkcijama preslikavanja fizičke površi Zemlje na ravan (površ koja odvaja tvrd i tečan površinski deo naše planete od njene atmosfere). Fizička površ Zemlje zbog velike nepravilnosti i složenosti ne može se matematički izraziti, moraju se, najpre, sve tačke i mereni podaci svesti ortogonalnim projiciranjem ‒ normalama na površ nekog pravilnog geometrijskog tela dovoljno bliskog Zemlji po obliku i dimenzijama i zatim je preslikati na ravan, Slika 1.29.
Planeta Zemlja se najčešće aproksimira referentnim površima i to geoidom, elipsoidom, sferom i ravnom površi (ravan). Složenost aproksimacije je korelisana i sa složenošću računanja na referentnoj površi (Varga 2021), Slika 1.30.
Aproksimacija planete Zemlje
Geoid je najrealnija aproksimacija Zemlje, nije simetričan i veoma je kompleksan da se opiše matematički. Geoid je ekvipotencijalna površ, na koju je, u svakoj njenoj tački, pravac sile teže upravan. Geoid, koji se na okeanima poklapa sa nivoom vode mora i okena, ako bi se taj nivo produžio ispod kontinenata, tako da je u svakoj njegovoj tački sila teže usmerena po normali, dobio bi se geoid (u stvari, normalna je na tangentu ravan geoida u tački posmatranja). Površ geoida, iako glatka, zbog neregularnog rasporeda i gustine zemljinih masa ima niz talasa (undulacija), tj. vrlo je složenog oblika (Slika 1.31); nesimetrična je u odnosu na obrtnu osu (Jovanović 1984).
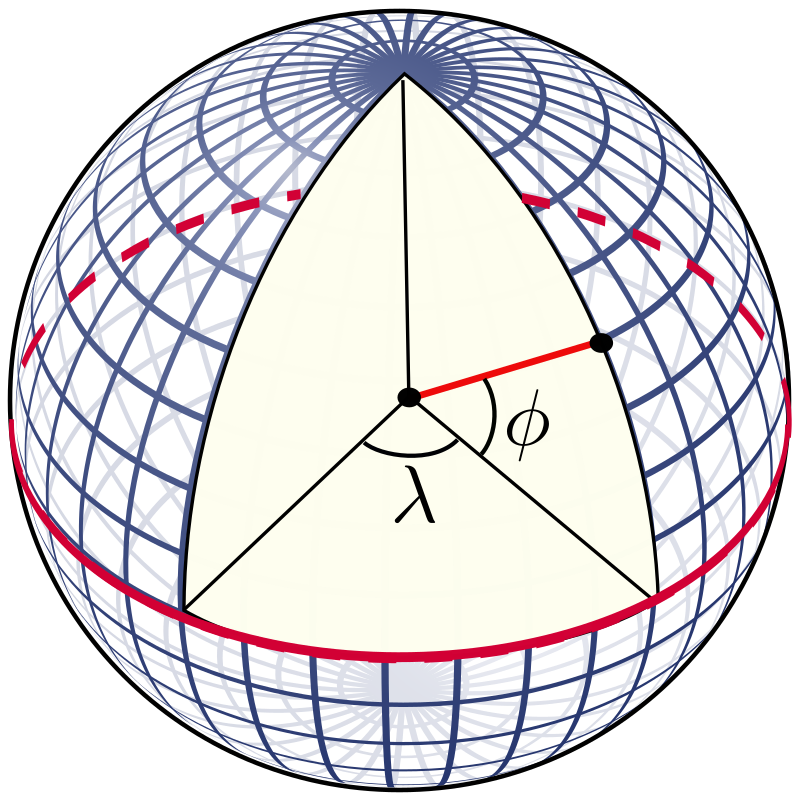
Geoid je veoma pogodan za izučavanje polja sile Zemljine teže, ali je njegova površ nepravilna i matematički se ne može izraziti u celini, pa jednačine za određivanje koordinata tačaka, dužina i uglova postaju neupotrebljive. Samo visine tačaka, odnosno rastojanja između geoida i fizičke površi Zemlje, uzeta duž vertikala odnosnih tačaka, pogodne su za korišćenje u matematičkoj kartografiji. Dakle, uglavnom imamo krivolinijske koordinate na sferi ili još češće na elipsoidu, i te koordinate su zadate uglovnim vrednostima, geodetskom širinom i dužinom, \(\phi\) i \(\lambda\) , Slika 1.32. U narednom poglavlju će se detaljnije objasniti pojam koordinata i računanja na sferi i elipsoidu.
Prvi ili direktni zadatak matematičke kartografije
Direktni zadatak podrazumeva preslikavanje koordinata sa elipsoida (ili sfere) na ravan karte koristeći matematičke funkcije preslikavanja. Preslikavanje redovno prate neizbežne deformacije, čiji se raspored i iznosi mogu odrediti ako se poznaje funkcija (zakon) preslikavanja. Funkcije preslikavanja, gde je \(E\) pravougla koordinata u pravcu istoka, \(N\) pravougla koordinata u pravcu severa u ravni karte, a elipsoidne koordinate sa geodetskom širinom i dužinom su \(\phi\) i \(\lambda\) :
\[E = f_{1}(\varphi,\lambda)\] \[N = f_{2}(\varphi,\lambda)\]
Deformacije dužina, uglova i površina su poznate za bilo koju tačku na karti. Funkcije preslikavanja se nazivaju kartografske projekcije. Matematička kartografija se uglavnom bavi izučavanjem kartografskih projekcija. Ilustrtacija direktnog zadatka data je na sledećoj slici, Slika 1.33.
Drugi ili inverzni zadatak matematičke kartografije
Inverzni zadatak podrazumeva preslikavanje koordinata koristeći matematičke funkcije preslikavanja iz ravni karte na elipsoid (ili sferu). Funkcije preslikavanja:
\[\phi = g_{1}(E,N)\] \[\lambda= g_{2}(E,N)\]
Slika 1.34 prikazuje ilustraciju inverznog zadatka.
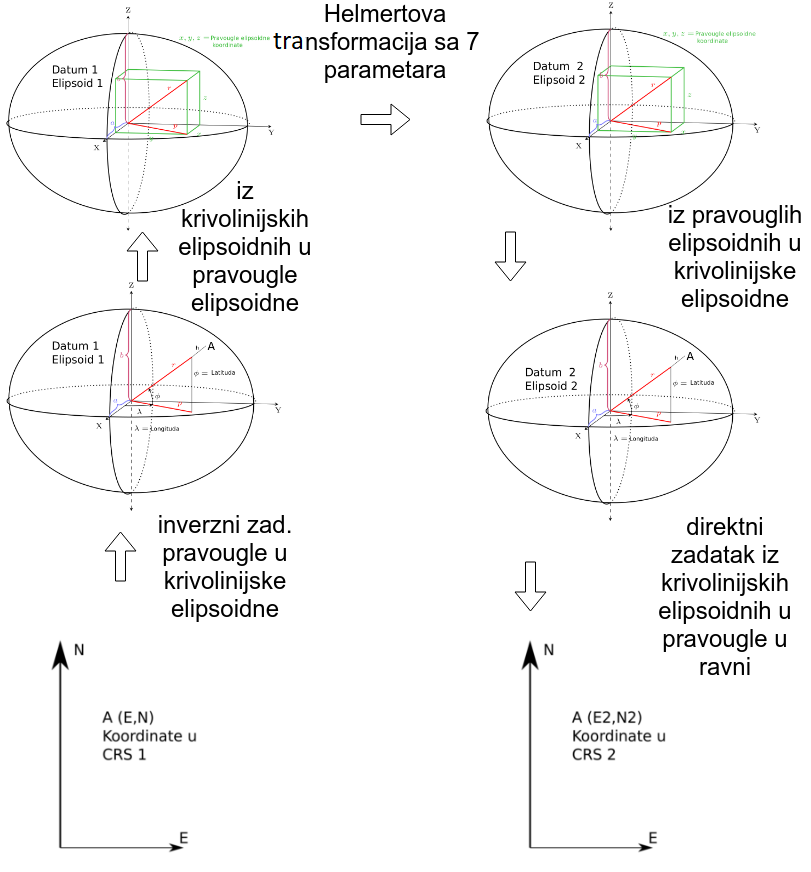
Koordinatne transformacije iz jednog koordinatnog sistema u drugi
Vrlo često imamo potrebu da se koordinate transformišu iz jednog koordinatnog sistema u drugi, o tome će biti reči u nekom od narednih poglavlja, ovde je samo data ilustracija, Slika 1.35.
1.8 Istorija matematičke kartografije
U ovom delu taksativno su dati samo najvažniji događaji iz istorije razvoja matematičke kartografije, ovaj pregled je većim delom baziran na knjizi Matematatička kartografija(Jovanović 1984):
Saznanje da je Zemlja zakrivljena površ, ovo mišljenje najpre se utvrđuje među učenicima grčkog naučnika Pitagore (sa ostrva Samosa, 6. v. pre n.e.);
Prvi dokazi o Zemlji kao lopti potiču od Aristotela (384‒322. g. pre n.e.), koji smatra da je dužina meridijana 400.000 stadija, odnosno 63.200 km i zastupa tezu o geocentričnosti svemira;
Određivanje dužine meridijana i utvrđivanje radijusa Zemljine lopte; ove vrednosti znatno tačnije od Aristotela utvrdio je Eratosten iz Kirene (276‒194), čuveni astronom, geograf i upravnik Aleksandrijske biblioteke. Dimenzije Zemlje Eratosten određuje merenjem meridijanskog luka između Sijene i Aleksandrije u Egiptu. Njegovi rezultati, relativno gledano, znatno se približavaju današnjim vrednostima (prema Eratostenu, obim Zemlje iznosi 252.000 stadija ili 39.186 km);
Kako je Eratosten izračunao obim Zemlje? Eratosten je čuo da u Sijeni, gradu južno od Aleksandrije, ne postoje senke vertikalnih objekata na dan letnje ravnodnevice, tj. kada je Sunce u zenitu. Pitao se da li je ista situacija i u Aleksandriji pa da je 21. juna zabo štap u tle i posmatrao senku na zemlji. Senka je padala pod uglom od 7,2 stepena. Pošto sunčevi zraci padaju na tle pod istim uglom u isto doba istog dana, a štap u Aleksandriji ima senku dok onaj u Sijeni nema, to znači da je površina Zemlje zakrivljena. Eratosten je to verovatno već znao, prateći učenje Pitagore. Ako je Zemlja sfera, Eratosten je znao da može izračunati njen obim. Pošto je razlika u dužini senki bila oko 7 stepeni, to znači da su ova dva mesta oko 7 stepeni udaljena na Zemljinoj površini od 360 stepeni. Eratosten je platio čoveku da izmeri rastojanje od Aleksandrije do Sijene. Rastojanje je bilo 5.000 stadija, tj. oko 800 km, Slika 1.36.
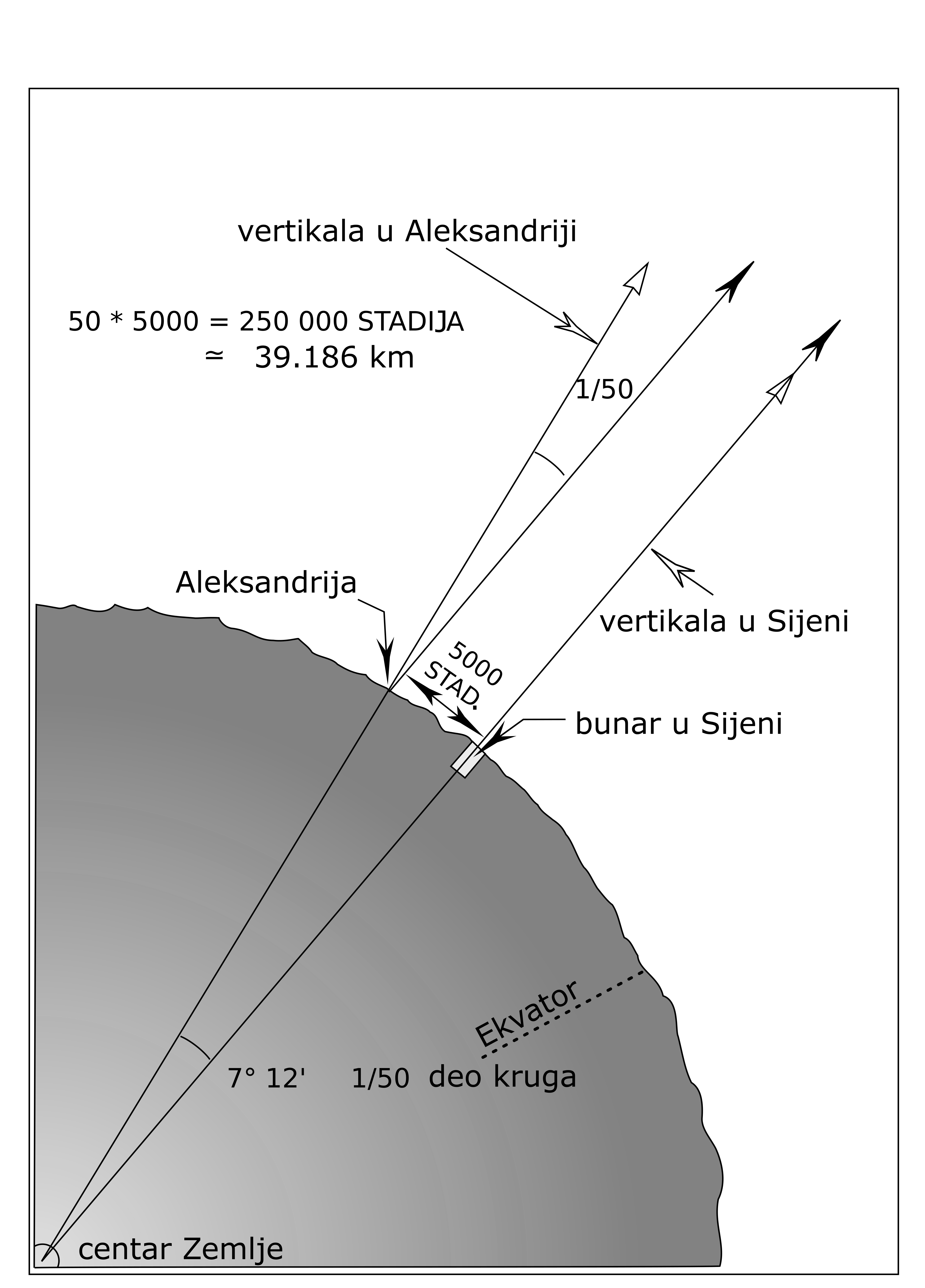
Preko jednostavnog računanja proporcija našao je obim Zemlje ‒ 7,2 stepena je 1/50 deo od 360 stepeni, a kada se 50 pomnoži sa 800 dobija se 40.000 km.
Izrada prvog Zemljinog globusa pripisuje se Kratesu sa ostrva Malos (2. v. pre n.e.),
Predlog da se položaji tačaka na površi Zemljine lopte utvrđuju geografskim koordinatama ‒ širinom i dužinom ‒ koji potiče od Hiparha (160‒125. p.n.e.).
Najstarija kartografska projekcija (gnomonska ili centralna), pripisuje se Talesu iz Mileta (639‒548 p.n.e.), a korišćena je za kartu zvezdanog neba. Zatim sledi ortografska projekcija koju je predložio Apolonije iz Perga (262‒190. p.n.e.), pa stereografska projekcija koju je obradio Hiparh (već pomenuti grčki naučnik iz 2. v. pre n.e.) i koristio je za izradu svoje geografske karte. Hiparh je, takođe, razradio ortografsku perspektivnu projekciju, kao i prostu konusnu projekciju, i ukazao na metod sastavljanja karata na osnovu astronomskih tačaka.
Kod antičkih i rimski naučnika radovi aleksandrijskog matematičara Klaudijusa Ptolemeja (90‒168. g. nove ere) on uvodi dve nove kartografske projekcije koje se primenjuju i danas (tzv. ekvidistantna konusna projekcija ‒ Ptolemeja i ekvivalentna konusna projekcija ‒ Ptolemeja, čija je glavna svojstva, mnogo vekova kasnije, iskoristio za razradu svoje projekcije francuski geograf Bone ‒ 1752. god.).
U istoriji kartografije srednjeg veka, Merkatorovo ime zauzima najistaknutije mesto. Holandski kartograf Merkator (Gerhard Kremer-Merkator, 1512‒1594) već je razvio konformnu cilindričnu projekciju, koja se, iako ima znatne deformacije površina na srednjim i velikim širinama, zbog dobrih svojstava za navigaciju, i danas primenjuje za izradu pomorskih i vazduhoplovnih karata, a veoma je popularna i u veb-kartografiji za portale koji prikazuju globalne podatke.
Za stvaranje geodetske osnove premera, u to vreme, već se primenjuje postupak triangulacije, koji je predložio W. Snellius (1615), kao i metodi astronomskog određivanja geodetskih koordinata. Topografske karte ovog perioda izrađuju se u poprečnoj ekvidistantnoj cilindričnoj projekciji Kasini-Soldnera (Kassini-Soldner), odnosno u pseudokonusnoj Bonovoj projekciji.
Na razradi teorije kartografskih projekcija u XVIII i XIX veku, pored izrazito kartografskih stručnjaka, radio je i veliki broj drugih stručnjaka, osobito matematičara, kao na primer: J. L. Lagrange (1736‒1813), J. H. Lambert (1728‒1777), L. Euler (1707‒1783) i dr.
Nemački naučnik Gaus (Carl Friedrich Gauss, 1777‒1855) razrešio je problem opšte teorije konformnog preslikavanja jedne površi na drugu i u okviru toga preslikavanje elipsoida (sferoida) na loptu. Opšte rešenje Gaus je kasnije razradio za praktičnu primenu u oblasti računske obrade geodetskih merenja, primenivši ga najpre za računanje triangulacije razvijene na području grada Hanovera. Konformna, poprečna cilindrična projekcija, koju je obradio Gaus (tzv. Gaus-Krigerova projekcija, njena modifikacija je i UTM projekcija) našla je, u savremenim uslovima, primenu u mnogim zemljama sveta, kao osnovna državna projekcija.
Pred kraj XIX veka francuski geograf Tiso (Auguste Tissot, 1824‒1897) definitivno je uobličio opštu teoriju deformacija. Smatra se da njegovo delo ima fundamentalan značaj za područje matematičke kartografije u kome se razmatraju deformacije koje neizbežno nastaju pri preslikavanju Zemljinog elipsoida ili lopte u ravan.
Bivand, Roger, Jakub Nowosad, and Robin Lovelace. 2022. spData: Datasets for Spatial Analysis. https://jakubnowosad.com/spData/.
Brown, Lloyd Arnold. 1979. The Story of Maps. Courier Corporation.
Jovanović, Velibor. 1984. Matematička Kartografija. VGI.
Kilibarda, Milan, and Dragutin Protić. 2018. Geovizualizacija i Web Kartografija. Univerzitet u Beogradu, Građevinski fakultet. http://osgl.grf.bg.ac.rs/books/gvvk/index.html.
Pebesma, Edzer, Wolfgang Wagner, Jan Verbesselt, Erwin Goor, Christian Briese, and Markus Neteler. 2016. “OpenEO: A GDAL for Earth Observation Analytics.” https://www.r-spatial.org/2016/11/29/openeo.html. 2016. https://www.r-spatial.org/2016/11/29/openeo.html.
Varga, Matej. 2021. “Geometrijska geodezija: Glavni geodetski zadatci, transformacije i konverzije koordinata, Priručnik algoritama i numeričkih primjera.” Unpublished. https://doi.org/10.13140/RG.2.2.17926.70725.