4 Cilindrične projekcije
Geometrijski, cilindrične projekcije mogu se delimično razviti pomoću plašta cilindra koji je bio omotan oko sfere (elipsoida) koji predstavlja Zemlju, a dodiruje se na Ekvatoru sa cilindrom, meridijani i paralele projiciraju se iz centra sfere na plašt cilindra. Cilindrične projekcije imaju veliki značaj u matematičkoj kartografiji. Pored podele cilindričnih projekcija, u ovom poglavlju su detaljno predstavljene prave cilindrične projekcije sa izvođenjem formula za opšti slučaj svih pravih cilindričnih projekcija. Detaljno su razrađene prave konformne cilindrične projekcije za slučaj dodirnog (Merkatorova projekcija) i sekućeg cilindra. Razrada drugih oblika cilindričnih projekcija nije data, ali principijelno izvođenje predstavljeno za slučaj Merkatorove projekcije može se primeniti na sličan način kod svih ostalih cilindričnih projekcija. Na kraju ovog poglavlja sledi 8 primera za računanje direktnog, inverznog zadatka, kao i pratećih deformacija.
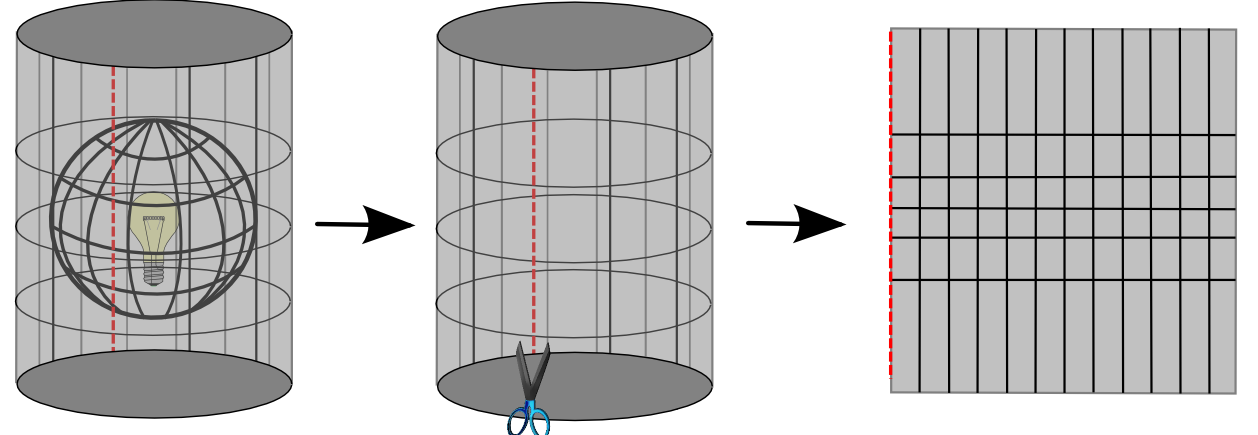
Kao što je već pomenuto, mreža meridijana i paralela kod cilindričnih projekcija najočiglednije se predstavlja kao projiciranje površi Zemljine lopte ili elipsoida na plašt cilindra, koji se potom razvija na ravan, Slika 4.1. U prošlosti se preslikavanje vršilo postupcima koji se baziraju na primeni linearne perspektive. Razvojem matematike i matematičke kartografije ovo preslikavanje se definiše analitičkim funkcijama preslikavanja uz unapred definisane uslove preslikavanja. Tako na primer kod pravih konformnih cilindričnih projekcija imamo da se dodirna paralela cilindra i elipsoida preslikava bez linearnih deformacija i da je projekcija konformna, tj. da je linearna razmera u svim pravcima ista.
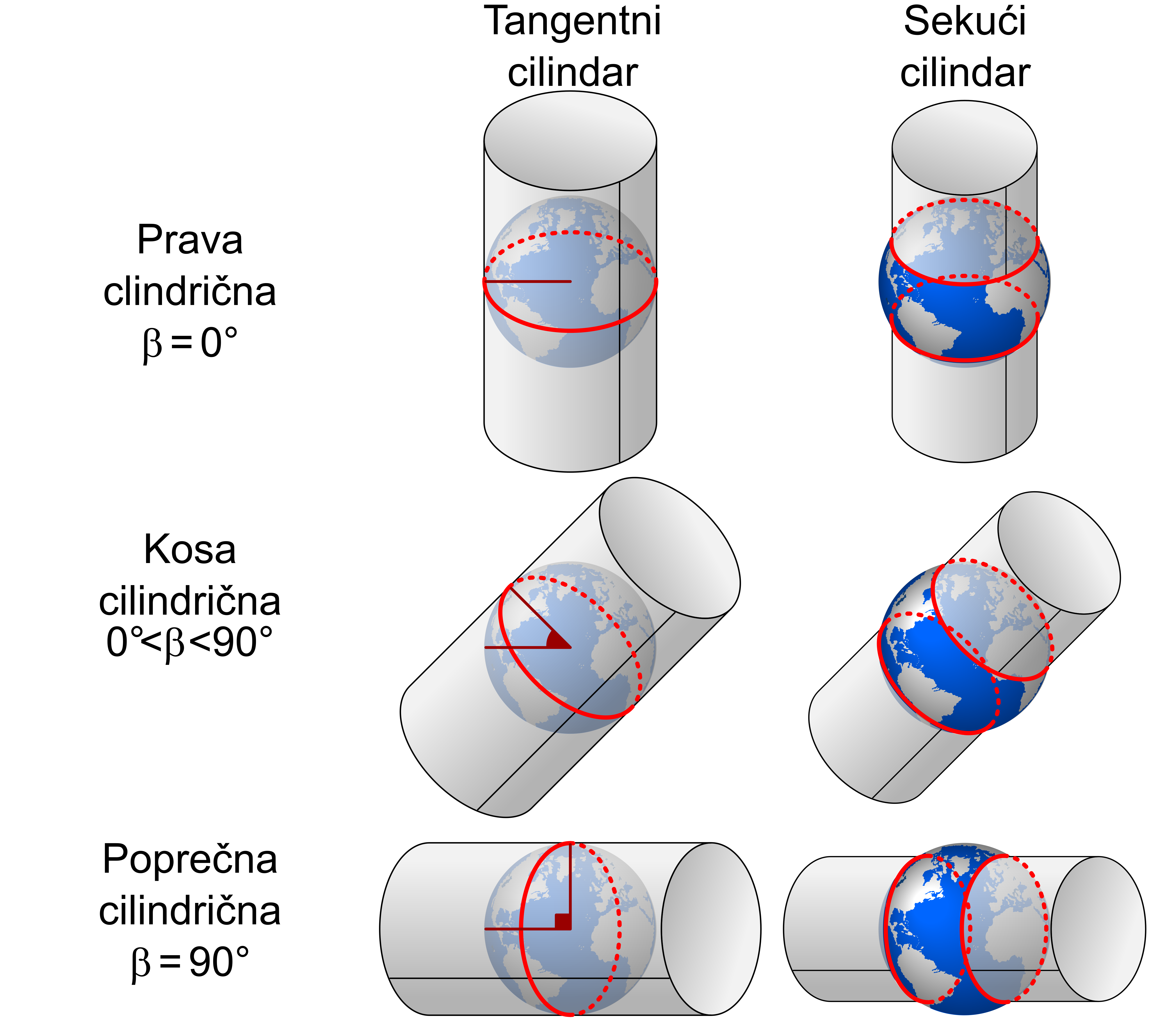
Cilindar može biti tangirajući ili sekući i zauzimati normalan (prav, uspravan), kos ili poprečan (transferzalan) položaj u odnosu na površ Zemljinog elipsoida ili lopte, Slika 4.2. U pravim cilindričnim projekcijama Ekvator je dodirna, standardna paralela, i on se preslikava kao prava linija, najčešće bez deformacija dužina. Kad imamo sekući cilindar, obe sekuće paralele su standardne paralele, tj. preslikavaju se bez deformacija.
U odnosu na deformacije, cilindrične projekcije mogu biti: konformne, ekvivalentne i uslovne.
4.1 Prave cilindrične projekcije
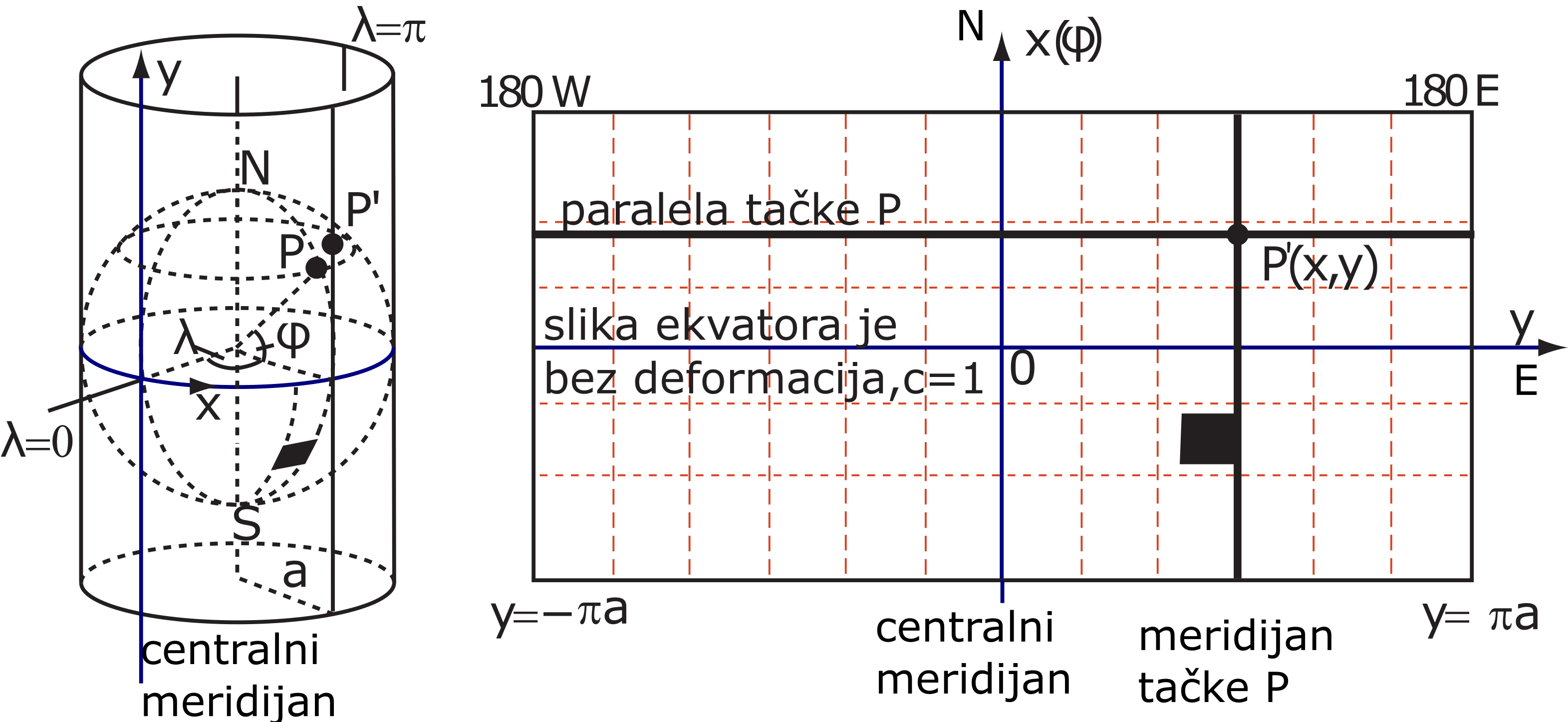
Kod pravih cilindričnih projekcija osa rotacije elipsoida (ili sfere) poklapa se sa osom cilindra. Koordinatne ose su Ekvator i početni meridijan (Grinički meridijan) ili srednji meridijan područja preslikavanja. Mreža meridijana i paralela preslikava se kao prave ortogonalne linije, dok se polovi preslikavaju u beskonačnost, tj. nemaju sliku u ravni karte, Slika 4.3. Može se uočiti (Slika 4.3) da opšte formule svih pravih cilindričnih projekcija možemo definisati na sledeći nanačin:
\[ \begin{gathered} x=N=f(\varphi) \\ y=E=k \lambda \end{gathered} \]
Oblik funkcije preslikavanja \(x=N=f(\varphi)\) određuje se zavisno od zadatih uslova preslikavanja, pa razlikujemo: konformne, ekvivalentne ili uslovne (najčešće ekvidistantne) prave cilindrične projekcije. Koordinata u pravcu istoka zavisi od konstante \(k\) koja određuje koliki je razmak između slika meridijana u ravni karte, takođe konstanta \(k\) zavisi od uslova koji se postavljaju prilikom preslikavanja elipsoida ili sfere na ravan karte.
Kako je mreža meridijana i paralela kod pravih cilindričnih ortogonalna, baš kao i na elipsoidu, onda se u pravim cilindričnim projekcijama glavni pravci poklapaju sa pravcima meridijana i paralela, pa će se ose elipse deformacija nalaziti u pravcu meridijana i paralela. Ugao između meridijana i paralela u projekciji je \(\theta=90^o\), ako to uvrstimo u formulu za linearnu deformaciju, imamo:
\[ c^2=m^2 \cos ^2 \alpha+m n \cos (90^o) \sin 2 \alpha+n^2 \sin ^2 \alpha \]
očigledno je da su glavni pravci \(m\) i \(n\):
\[ c^2=m^2 \cos ^2 \alpha+n^2 \sin ^2 \alpha \]
Razmer površina definisan izrazom:
\[ p=m n \sin \theta= m n \sin (90^o) =m n=a b \]
Ako uočimo, Slika 4.4, preslikavanje elementarnog elipsoidnog trapeza u ravan prave cilindrične projekcije, možemo definisati formule za računanje linearnog razmera u pravcu meridijana i paralele.
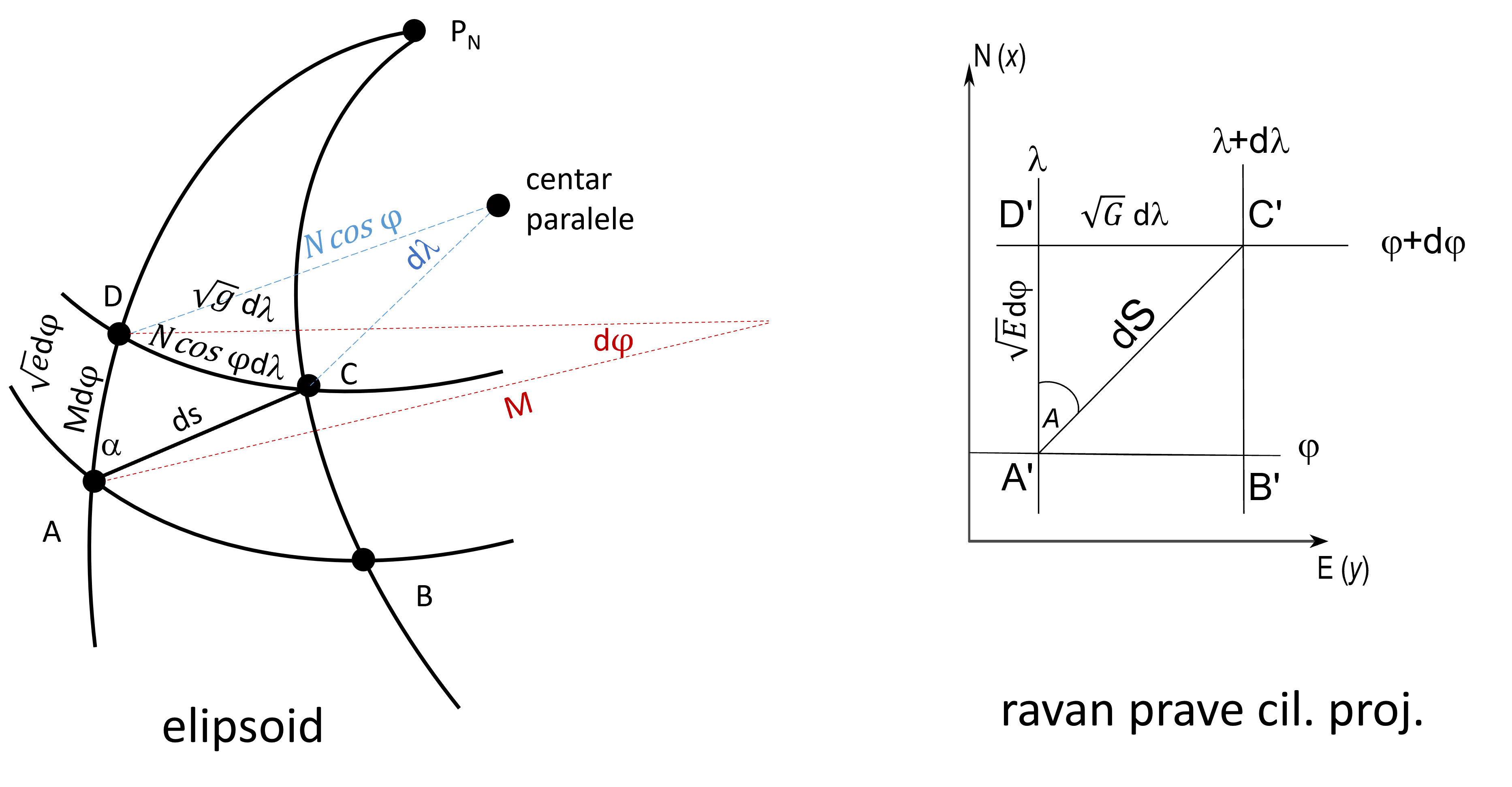
Kao što smo videli u poglavlju Opšte jednačine kartografskih projekcija 3.3, Gausove fundamentalne veličine imaju oblik :
\[ E=\left(\frac{\partial x}{\partial \varphi}\right)^2+\left(\frac{\partial y}{\partial \varphi}\right)^2 \]
\[ G=\left(\frac{\partial x}{\partial \lambda}\right)^2+\left(\frac{\partial y}{\partial \lambda}\right)^2 \]
Parcijalni izvodi funkcija preslikavanja koje možemo odrediti su:
\[ \frac{d x}{d \lambda}=0 \]
\[ \frac{d y}{d \varphi}=0 \]
\[ \frac{d y}{d \lambda}=k \]
Dalje je:
\[ \sqrt{E}=\frac{d x}{d \varphi} \]
\[ \sqrt{G}=\frac{d y}{d \lambda}=k \]
Sa sike (Slika 4.4, a i ranije iz poglavlja Opšte jednačine kartografskih projekcija 3.4.2.1) jasno je da je linearna razmera u pravcu meridijana i paralele:
\[ m=\frac{\sqrt{E}}{M} \]
\[ n=\frac{\sqrt{G}}{N \cos \varphi} \]
Ako zamenimo vrednosti Gausovih fundamentalnih veličina u prethodnim formulama, dobićemo:
\[ m=\frac{d x}{M d \varphi} \]
\[ n=\frac{k}{N \cos \varphi} \]
Sada možemo dobiti i formulu za razmer površina:
\[ p=a b=m n=\frac{k d x}{N M \cos \varphi d \varphi} \]
Konačno možemo grupisati opšte formule pravih cilindričnih projekcija:
\[ x=f(\varphi) \]
\[ y=k \lambda \]
\[ m=\frac{d x}{M d \varphi} \]
\[ n=\frac{k}{r}=\frac{k}{N \cos \varphi} \]
\[ p=a b=m n=\frac{k d x}{N M \cos \varphi d \varphi} \]
\[ \operatorname{tan} \frac{\omega}{2}=\frac{a-b}{2 \sqrt{a b}}=\frac{m-n}{2 \sqrt{m n}} \]
\[ \sin \frac{\omega}{2}=\frac{a-b}{a+b}=\frac{m-n}{m+n} \]
Iz gore navedenih formula možemo zaključiti da:
U pravim cilindričnim projekcijama deformacije linijskih elemenata, a takođe i površina i uglova, zavise isključivo od geodetske širine.
Izokole (linija jednakih deformacija) su paralelne prave linije koje se poklapaju sa paralelama.
Prave cilindrične projekcije najpodesnije su za karte teritorija izduženih u pravcu paralela.
Ako znamo formule za preslikavanje sa elipsoida, veoma je jednostavno definisati i formule za preslivanje sa sfere na ravan karte. Samo za ovu projekciju će i one biti navedene:
\[ \begin{aligned} & x=f(\varphi) \\ & y=k \lambda \\ & m=\frac{d x}{R d \varphi} \\ & n=\frac{k}{r}=\frac{k}{R \cos \varphi} \\ & p=a b=\frac{k d x}{R^2 \cos \varphi d \varphi} \\ & \sin \frac{\omega}{2}=\frac{a-b}{a+b}=\frac{m-n}{m+n} \end{aligned} \]
4.2 Prava konformna cilindrična projekcija ‒ Merkatorova projekcija
Prava konformna cilindrična projekcija ili Merkatorova projekcija jedna je od najznačajnih projekcija u istoriji kartografije. Ova se projekcija i danas intenzivno koristi za prikaz karte sveta, a posebno kod veb-karata. Karte sa veb-kartografskih portala https://www.openstreetmap.org/ ili https://maps.google.com/ su u Merkatorovoj projekciji. O značaju ove projekcije biće reči kasnije.
Eksplicitan oblik funkcije preslikavanja \(x=f(\varphi)\) i konstante \(k\) tražićemo tako da je zadovoljen uslov konformnosti: \(m=n\). Tada imamo:
\[ \frac{d x}{M d \varphi}=\frac{k}{N \cos \varphi} \]
Dalje sledi:
\[ d x=k \frac{M}{N} \frac{d \varphi}{\cos \varphi} \]
Da bismo dobili zatvorenu formulu za funkciju \(x\) neophodno je rešiti integral:
\[ q=\int \frac{M d \varphi}{N \cos \varphi} \]
Veličina \(q\) se naziva konformna ili izometrijska širina i veoma je značajna kod svih konformnih preslikavanja.
Ako uočimo elementarni trapez na elipsoidu (Slika 4.4), možemo definisati linijski element:
\[ {ds}^2=(\mathrm{Md} \varphi)^2+(N \cos \varphi \mathrm{d} \lambda)^2 \]
ili:
\[ d s^2=r^2\left(\frac{M^2}{r^2} d \varphi^2+d \lambda^2\right) \]
gde je r poluprečnik krivine paralele (\(r= N \cos \varphi\)).
Ako sa \(dq\) označimo veličinu \(\frac{M}{r} d \varphi\), dobijamo:
\[ d s^2=r^2\left(d q^2+d \lambda^2\right) \]
Veličina \(q\) se naziva izometrijska ili konformna širina.
\[ dq= \frac{M d \varphi}{N \cos \varphi}=\frac{M}{r} d \varphi \]
Ako se osvrnemo na prethodno poglavlje, znamo da veličine za poluprečnik krivine prvog vertikala i meridijana imaju oblik:
\[ N(\varphi)=\frac{a}{\sqrt{1-e^2 \sin ^2 \varphi}} \]
\[ M(\varphi)=\frac{a\left(1-e^2\right)}{\left(1-e^2 \sin ^2 \varphi\right)^{\frac{3}{2}}} \]
gde je prvi numerički ekscentricitet definisan izrazom:
\[ e^2=\left(a^2-b^2\right) / a^2 \]
Jasno je da veličina \(dq\), pa samim tim i \(q\), isključivo zavisi od geodetske širine, a možemo uočiti da je to nelinearna funkcija od geodetske širine.
Izometrijska širina
Izometrijska širina (\(q\)) je nelinearna funkcija geodetske širine koja je direktno proporcionalna razmaku paralela, u odnosu na Ekvator, u elipsoidnoj Merkatorovoj projekciji. To je bezdimenzionalna veličina. Za razliku od drugih tipova pomoćne geodetske širine, izometrijska širina nije ugaona. Na severnom polu njena vrednost je beskonačno, dok je njena vrednost na južnom polu minus beskonačno.
Ako zamenimo vrednosti M i N u izrazu \(dq= \frac{M d \varphi}{N \cos \varphi}\) dobija se:
\[ q=\frac{\left(1-e^2\right) d \varphi}{\left(1-e^2 \sin ^2 \varphi\right) \cos \varphi} \]
Jasno je da važi i izraz \(e^2=e^2\left(\sin ^2 \varphi+\cos ^2 \varphi\right)\) pa dalje imamo:
\[ \frac{1-e^2}{1-e^2 \sin ^2 \varphi}=\frac{1-e^2 \sin ^2 \varphi-e^2 \cos ^2 \varphi}{1-e^2 \sin ^2 \varphi} \]
Ako se vratimo na \(dq\) biće:
\[ d q=\frac{d \varphi}{\cos \varphi}-\frac{e^2 \cos \varphi d \varphi}{1-e^2 \sin ^2 \varphi} \]
Tako da izometrijsku širinu možemo definisati kao:
\[ q=\int \frac{d \varphi}{\cos \varphi}-e \int \frac{e \cos \varphi d \varphi}{1-e^2 \sin ^2 \varphi} \]
Rešenje ovog integrala može se naći u literaturi za matamatičku kartografiju (Jovanović 1984; Bugayevskiy and Snyder 2013; Snyder 1987; Krakiwsky 1973).
Uvedemo li smenu:
\[ e \sin \varphi=\sin \psi \]
odnosno, ako diferenciramo:
\[ e \cos \varphi d \varphi=\cos \psi d \psi \]
dalje na osnovu osnovnog trigonometrijkog identiteta:
\[ 1-e^2 \sin ^2 \varphi=\cos ^2 \psi \]
\[ q=\int \frac{d \varphi}{\cos \varphi}-e \int \frac{d \psi}{\cos \psi} \]
Dakle rešenje će se dobiti ako se reši integral:
\[ \int \frac{1}{\cos x} d x \]
Ako zapišemo ovaj integral na sledeći način, imamo:
\[ \int \frac{1}{\cos x} d x=\int \frac{1}{\sin \left(x+\frac{\pi}{2}\right)} d x=\int \frac{1}{\sin t} d t \]
\[ t=x+\frac{\pi}{2} \]
Ako uvedemo sledeću smenu:
\[ u=\tan \frac{t}{2} \]
Onda je:
\[ \int \frac{1}{\frac{2 u}{1+u^2}} \cdot \frac{2}{1+u^2} d u=\int \frac{1}{u} d u=\ln |u|+C=\ln \left|\tan \left(\frac{x}{2}+\frac{\pi}{4}\right)\right|+C \]
Gde je C konstanta integracije. Konačno, rešenje za izometrijsku širinu je:
\[ q=\ln \operatorname{tan}\left(45^{\circ}+\frac{\varphi}{2}\right)-e \ln \operatorname{tan}\left(45^{\circ}+\frac{\psi}{2}\right)+C \]
Odnosno, ako sa U označimo razlomak:
\[ U=\frac{\operatorname{tan}\left(45^{\circ}+\frac{\varphi}{2}\right)}{\operatorname{tan}^{\mathrm{e}}\left(45^{\circ}+\frac{\psi}{2}\right)} \]
gde je \(e\) prvi numerički ekscentricitet meridijanske elipse (\(e^2=\left(a^2-b^2\right) / a^2\)) i \(\psi = arcsin(e \sin \varphi)\)
\[ q=\ln \mathrm{U}+C \]
Drugi način za rešavanje integrala:
\[ \int \frac{1}{\cos x} d x \]
Uvodimo smenu:
\[ u=\sin x \]
Dalje imamo:
\[ \mathrm{d} u=\cos x \mathrm{~d} x \] Tada imamo:
\[ \int \frac{\mathrm{d} x}{\cos x}=\int \frac{\cos x \mathrm{~d} x}{\cos ^2 x}=\int \frac{\mathrm{d} u}{1-u^2} \]
\[ \begin{aligned} & \frac{1}{1-u^2}=\frac{A}{1-u}+\frac{B}{1+u}=\frac{A(1+u)}{(1-u)(1+u)}+\frac{B(1-u)}{(1-u)(1+u)} \\ & =\frac{(A-B) u+(A+B)}{1-u^2} \\ & \end{aligned} \]
\[ \begin{gathered} A+B=1 \\ A-B=0 \Rightarrow A=B \\ 2 A=1 \Rightarrow A=1 / 2, B=\frac{1}{2} \end{gathered} \]
\[ \begin{gathered} \int \frac{1}{1-u^2}=\int \frac{\frac{1}{2}}{1-u} d u+\int \frac{\frac{1}{2}}{1+u} d u \\ =-\frac{1}{2} \int \frac{-1}{1-u} d u+\frac{1}{2} \int \frac{1}{1+u} d u \\ =\frac{1}{2} \ln (1+u)-\frac{1}{2} \ln (1-u)+C \\ =\frac{1}{2} \ln \left(\frac{1+u}{1-u}\right) \end{gathered} \]
\[ u=\sin x \]
Ovo se opet može svesti na rešenje koje smo dobili i na prvi način reševanja integrala, ali možemo i izbeći uvođenje promenljive \(\psi\), (dalje izvođenje bez uvođenja promenljive \(\psi\) može se pronaći kod Snyder (1987)):
\[ q=\ln U +C \]
Gde je:
\[ U=\left[\left(\frac{1-\sin \varphi}{1+\sin \varphi}\right)\left(\frac{1+e \sin \varphi}{1-e \sin \varphi}\right)^e\right]^{1 / 2} \] Ili u još jednom obliku \(U\) se može definisati formulom:
\[ U =\tan (\pi / 4-\varphi / 2) /[(1-e \sin \varphi) /(1+e \sin \varphi)]^{e / 2} \] gde je \(e\) prvi numerički ekscentricitet meridijanske elipse (\(e^2=\left(a^2-b^2\right) / a^2\)) i C konstanta integracije.
Kao što smo videli, da bismo do funkcije preslikavanja \(x\), imali smo \(d x=k \frac{M}{N} \frac{d \varphi}{\cos \varphi}\), neophodno je bilo rešiti izometrijsku širinu, tako da sada imamo:
\[ x=k \ln U+C \]
C je konstanta integracije, k je konstanta projekcije i U je definisano izrazom \(U=\frac{\operatorname{tan}\left(45^{\circ}+\frac{\varphi}{2}\right)}{\operatorname{tan}^{e}\left(45^{\circ}+\frac{\psi}{2}\right)}\) (\(e^2=\left(a^2-b^2\right) / a^2\)) , \(\psi = arcsin(e \sin \varphi)\)).
Kod prave konusne konformne cilindrične projekcije, Slika 4.3, imamo da je slika Ekvatora horizontalna osa koordinatnog sistema u ravni karte. Za tačke na Ekvatoru kad je \(\varphi= 0\) onda je \(lnU= ln1=0\). Vidimo i da je \(x\) na Ekvatoru 0, tako da je konstanta integracije \(C=0\), zato je funkcija \(x\):
\[ x=k \ln \frac{\operatorname{tg}\left(45^{\circ}+\frac{\varphi}{2}\right)}{\operatorname{tg}^{\mathrm{e}}\left(45^0+\frac{\psi}{2}\right)} \]
Grupisane formule za Merkatorovu projekciju
\[ x=k \ln \frac{\operatorname{tg}\left(45^{\circ}+\frac{\varphi}{2}\right)}{\operatorname{tg}^{\mathrm{e}}\left(45^0+\frac{\psi}{2}\right)} \]
\[ y=k \lambda \]
\[ m=n=\frac{k}{N \cos \varphi} \]
\[ p=a b=m n=\left(\frac{k}{N \cos \varphi}\right)^2 \]
\[ \omega=0 \]
Konstanta \(k\) se određuje tako što treba da bude ispunjen uslov da je linearna razmera jednaka 1 na standardnoj paraleli
\[ \frac{k}{N_0 \cos \varphi_0}=1 \]
\[ k=N_0 \cos \varphi_0 \] Ovo se odnosi na sekući cilindar, ako imamo slučaj da je cilindar dodirni, onda je \(\varphi_0=0\), cilindar dodiruje elipsoid po Ekvatoru, tada je:
\[ k=N \cos \varphi_0= N_0 = \frac{a}{\sqrt{1-e^2 \sin(0) ^2 }} = a \] Jasno je da je poluprečnik krivine prvog vertikala na ekvatorijalnom krugu jednak poluprečniku Ekvatora i bez prethodnog izvođenja.
Konačne formule za direktni zadatak matematičke kartografije za Merkatorovu projekciju su sledeće:
\[ x=a \ln \frac{\operatorname{tg}\left(45^{\circ}+\frac{\varphi}{2}\right)}{\operatorname{tg}^{\mathrm{e}}\left(45^0+\frac{\psi}{2}\right)} \]
\[ y=a \lambda \]
\[ m=n=\frac{a}{N \cos \varphi} \]
\[ p=a b=m n=\left(\frac{a}{N \cos \varphi}\right)^2 \]
\[ \omega=0 \] Jasno se vidi iz formula za računanje linerane razmere i razmera površina da se deformacije dužina i površina kod Merkatorove projekcije znatno uvećavaju kad udaljavamo od Ekvatora. Takođe je očigledno da je deformacija na polovima beskonačno velika. Vrlo često se koristi primer odnosa površine Afrike i Grenlanda u Merkatorovoj projekciji. Grenland je prikazan sa otprilike jednakom površinom kopna kao Afrika iako je površina Afrike aproksimativno 14 puta veća od Grenlanda, Slika 4.5. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 500 km na elipsoidu i odgovarajuće površine u projekciji.
library(sf)
library(spData)
# Koordinate za elipse deformacija
l = seq(-150,150, by=50)
f = c(-80, -65, -50, -30, -15, 0 , 15, 30, 50, 65, 80)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = 4326) # WGS84 koordinatni ref. sis.
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 500 km
tissot.sf = st_buffer(tissot.pt, dist = 500000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na elipsoidu
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u Merkatorovu projekciju
tissot.merc <- st_transform(tissot.sf, "+proj=merc +ellps=WGS84")
# površine u projekciji
tissot.merc$a_proj <- st_area(tissot.merc)
# odnos površina u projekciji i na elipsoidu
tissot.merc$p <- tissot.merc$a_proj/tissot.merc$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
world_m = st_transform(world,
crs = "+proj=merc +ellps=WGS84")
ll = st_centroid(tissot.merc)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(world_m), graticule = TRUE, border = 'gray', axes = TRUE)
plot(st_geometry(tissot.merc),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.merc$p,1)) ,col='red' , cex = 0.8)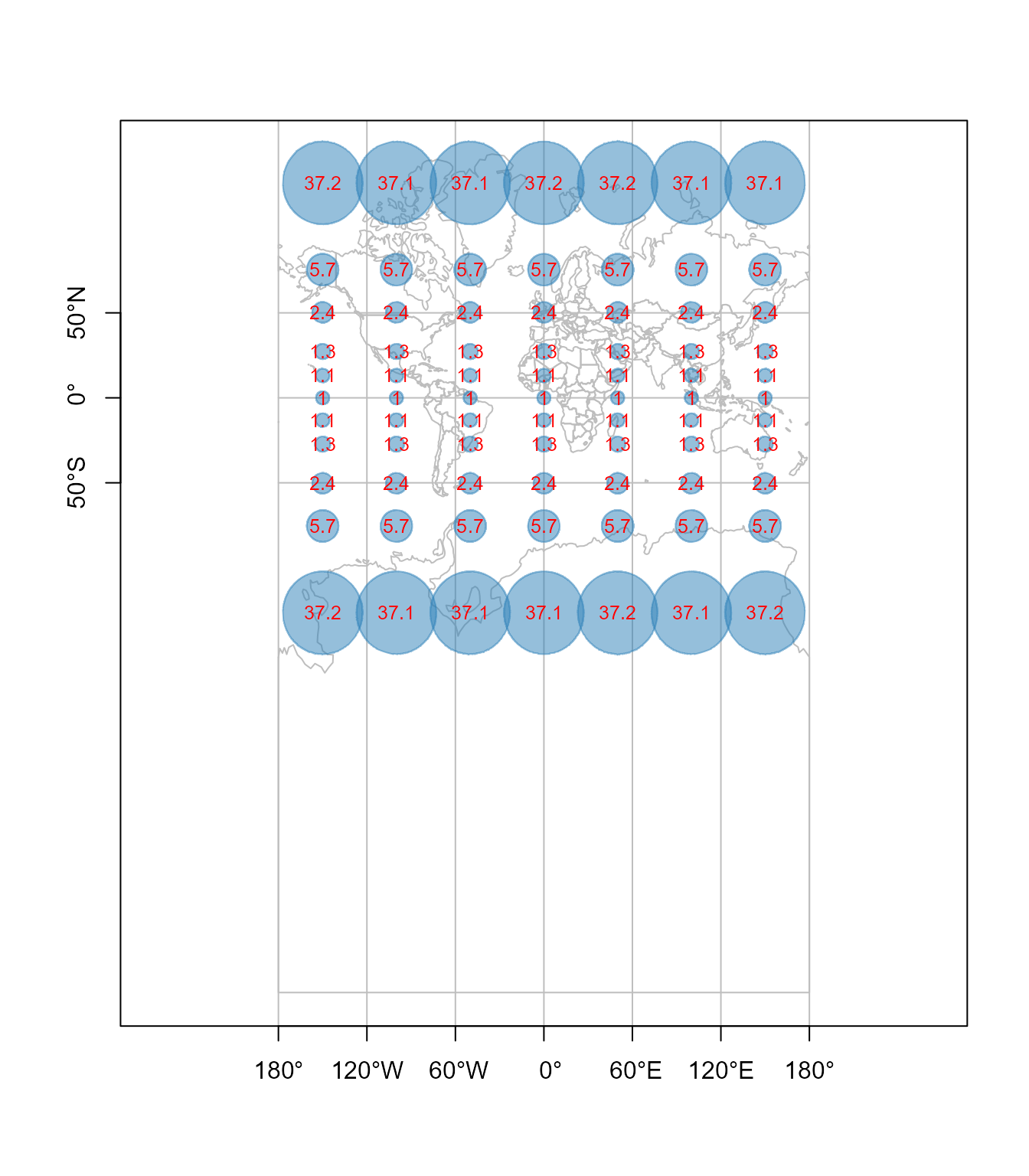
Konačne formule za direktni zadatak matematičke kartografije za pravu konformnu projekciju kad imamo sekući cilindar koji seče elipsoid po dve standardne paralele \(\varphi_0\) i \(-\varphi_0\) su:
\[ x=N_0 \cos \varphi_0 \ln \frac{\operatorname{tg}\left(45^{\circ}+\frac{\varphi}{2}\right)}{\operatorname{tg}^{\mathrm{e}}\left(45^0+\frac{\psi}{2}\right)} \]
\[ y=N_0 \cos \varphi_0 \lambda \]
\[ m=n=\frac{N_0 \cos \varphi_0}{N \cos \varphi} \]
\[ p=a b=m n=\left(\frac{N_0 \cos \varphi_0}{N \cos \varphi}\right)^2 \]
\[ \omega=0 \]
Sledeći primer, Slika 4.6, pokazuje elipse deformacija kad se koristi sekući cilindar koji seče elipsoid po dve standardne paralele, \(\varphi_0=50^o\) i \(\varphi_0=-50^o\). Kao što se vidi sa karte, dužine i površine se između standardnih paralela preslikavaju umanjeno u odnosu na elipsoid, dok se van standardnih paralela deformišu tako da su uvećane u odnosu na površine sa elipsoida. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 500 km na elipsoidu i odgovarajuće površine u projekciji. Na standardnim paralelama nema deformacija.
library(sf)
library(spData)
# longitude i latitude za el. def.
l = seq(-150,150, by=50)
f = c(-80, -65, -50, -30, -15, 0 , 15, 30, 50, 65, 80)
m = c()
# matrica lokacije elipsi def.
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima ćemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = 4326) # WGS84 koordinatni ref. sis.
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 500 km, kreiramo poligon od tacaka po krugu
tissot.sf = st_buffer(tissot.pt, dist = 500000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na elipsoidu
tissot.sf$a <- st_area(tissot.sf)
# treansformacija u Mer. sekući cilindar st. par. 50
tissot.merc <- st_transform(tissot.sf, "+proj=merc +lat_ts=50 +ellps=WGS84")
# površine u projekciji
tissot.merc$a_proj <- st_area(tissot.merc)
# odnos površina u projekciji i na elipsoidu
tissot.merc$p <- tissot.merc$a_proj/tissot.merc$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# transfomacija u u Mer. sekući cilindar st. par. 50
world_m = st_transform(world,
crs = "+proj=merc +lat_ts=50 +ellps=WGS84")
ll = st_centroid(tissot.merc)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(world_m), graticule = TRUE, border = 'gray', axes = TRUE)
plot(st_geometry(tissot.merc),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.merc$p,1)) ,col='red' , cex = 0.8)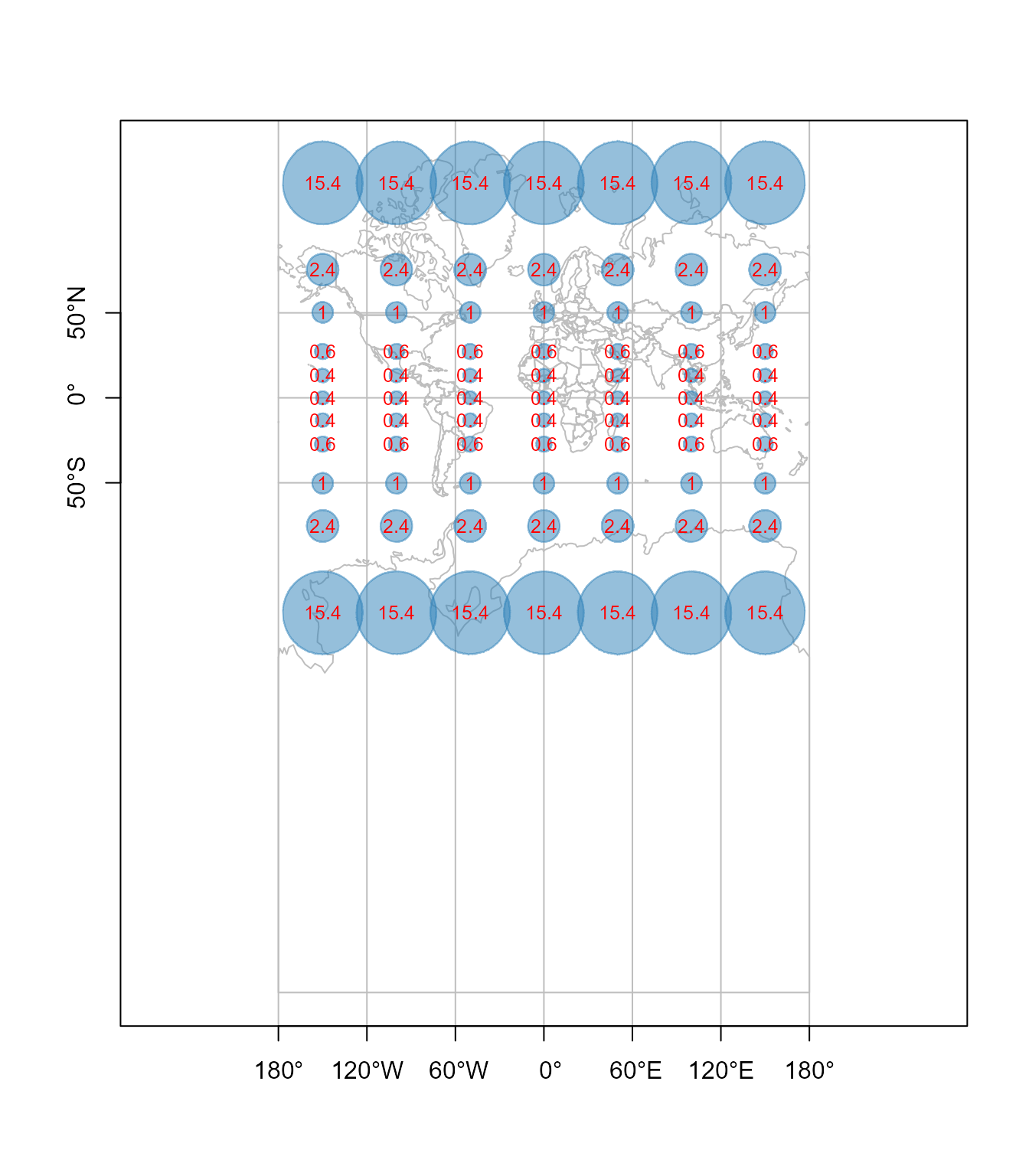
Formule za inverzni zadatak u opštem slučaju su:
\[ \lambda=y / k_0 \]
\[ \varphi=U^{-1}\left(\exp \left(-x / k_0\right)\right) \]
Gde je \(k_0=a\) ili kod sekućeg cilindra \(k_0=N_0 \cos \varphi_0\).
Značaj i primena Merkatorove projekcije
Prava konformna cilindrična projekcija u kartografskoj literaturi i pomorskoj praksi naziva se Merkatorovom projekcijom, prema latinskom prezimenu holandskog geografa i kartografa Gerhard Krämera (1512‒1594), koji je ovu projekciju prvi put primenio 1569. godine za kartu sveta. Ova karta smatrana je najvećim ostvarenjem u istoriji kartografije. Karta sveta (pomorska karta) pronađena je 1889. godine u Briselu, Slika 4.7. Kao originalna kreacija učinila je Merkatora čuvenim za sva vremena.
Istorijski razvoj projekcije dat je u knjizi Jovanović (1984): Svoje rezultate Merkator je najavio jednostavno kao „nov odnos i nov raspored meridijana prema paralelama“, imajući u vidu preslikavanje Zemljine lopte i ne dajući matematički izvod za konstrukciju paralela. U interesu istorijske istine treba istaći da su njegovi rezultati dobijeni približnim formulama. Trideset godina kasnije, engleski matematičar Edward Right, u svojoj publikaciji „Izvesne greške u navigaciji“, Cambrige 1599. god., objavio je znatno tačniji metod računanja sa tablicama za konstrukciju projekcije. Ipak, tek su radovi škotskog matematičara i fizičara Gregory Jamesa (1638‒1675) i njegov doprinos razvoju integrala omogućili da se matematički definitivno razradi i obrazloži zakon prave konformne cilindrične projekcije lopte na ravan.
Poslednjih godina, izbor projekcija za onlajn karte je bio raznolik. Međutim, preovlađujući izbor među većinom onlajn karata i veb-kartografskih servisa danas je Web Mercator (Merkatorova projekcija koja preslikava sferne koordinate sa lopte koja ima poluprečnik R iste veličine kao velika poluosa elipsoida WGS84, projekcija je poznata i pod nazivom Pseudo Merkatorova ili Web Merkatorova projekcija). Specifični razlozi iza ove preferencije u pogledu kartografije i računskih aspekata ostaju nepoznati. Ipak, ova projekcija je široko prihvaćen standard za globalne karte (kao i za tajlovane servise, videti npr. Kilibarda and Protić (2018), 16.7 Tajlovani lejer ili Peterson (2012)). Pseudo Merkatorova projekcija sod kada su je usvojile Google maps 2005. godine u EPSG notaciji ima oznaku EPSG:3857 (u proj4 notaciji je: +proj=merc +a=6378137 +b=6378137 +lat_ts=0 +lon_0=0 +x_0=0 +y_0=0 +k=1 +units=m +nadgrids=@null +wktext +no_defs +type=crs), a kod preslikavanja sa WGS84 elipsoida na ravan EPSG oznaka je EPSG:3395 (u proj4 notaciji je: +proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +datum=WGS84 +units=m +no_defs +type=crs), ovaj koordinatni referetni sistem ima naziv Svetska Merkatorova projekcija.Detaljno o korišćenju projekcija za veb-kartografiju može se dalje čitati u knjizi Lapaine and Usery (2017), poglavlje „Map Projections and the Internet“ (Kessler et al. 2017).
Geodetska linija i loksodroma u Merkatorovoj projekciji
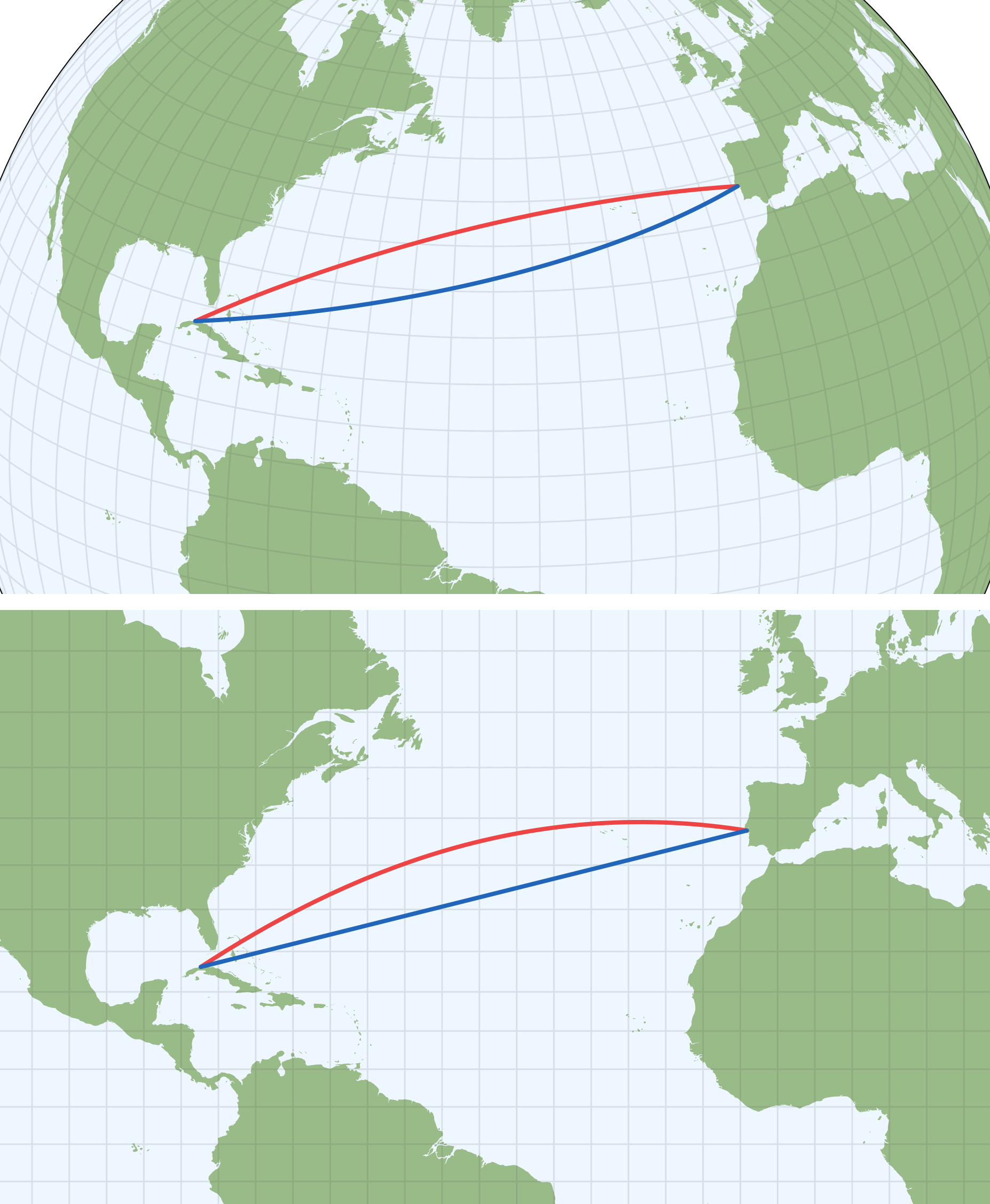
Najkraće rastojanje na Zemljinoj lopti je deo velikog kruga, tzv. ortodroma (engl.: great circle), koja se u projekciji najčešće prikazuje kao kriva linija višeg reda, pa je nepodesna za navigacijske ciljeve, jer zahteva neprekidno menjanje (određivanje) kursa. Jedino u kartama urađenim u centralnoj perspektivnoj (azimutnoj) projekciji ortodroma se preslikava kao približno prava linija, Slika 4.8 ‒ gore. U Merkatorovoj projekciji ortodroma je kriva linija (duža od loksodrome), sa konveksnom stranom okrenutom prema bližem polu. Loksodroma u Merkatorovoj projekciji preslikava se kao prava linija, Slika 4.8 ‒ dole. Zbog toga je ova projekcija bila veoma mnogo korišćena za navigaciju. Posebno za pomorske karte.
4.3 Merkatorova projekcija, primeri
U ovom delu dati su primeri direktnog zadatka (uključujući računanje pratećih deformacija) i obrnutog zadatka.
Primer 1: Računanje koordinata jedne tačke, direktni zadatak
Elipsoidne koordinate pozicije Građevinskog fakulteta u Beogradu (\(\varphi=44.8057705\) i \(\lambda=20.4759749\)) iz koordinatnog sistema WGS84 transformisati u Merkatorovu projekciju, Slika 4.9.
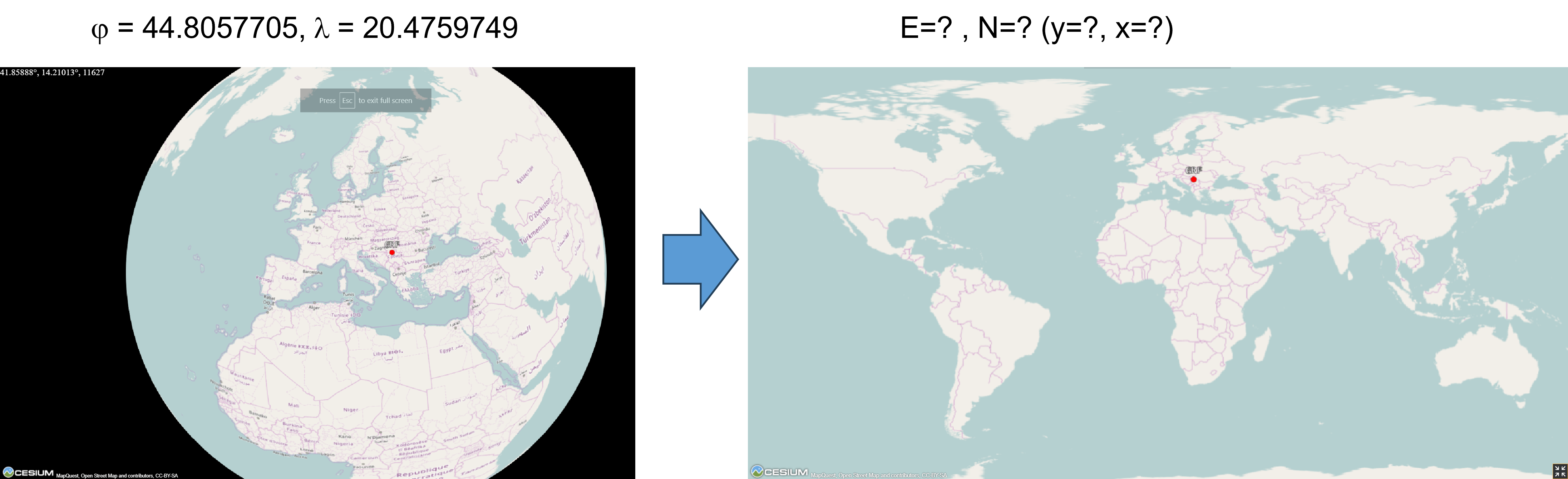
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = st_point( c(20.4759749, 44.8057705) ) # lon , lat
# potom pravimo kolekciju geometrije sfc
pts_sfc = st_sfc(grf, crs=4326)
# epsg kod 4326 je +proj=longlat +datum=WGS84 +type=crs
# transformacija u Merkatorovu projekciju
pts_sfc_M = st_transform(pts_sfc, crs = "+proj=merc +datum=WGS84")
pts_sfc_M
# Geometry set for 1 feature
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: 2279375.09936 ymin: 5560872.97673 xmax: 2279375.09936 ymax: 5560872.97673
# Projected CRS: +proj=merc +datum=WGS84
# matrica koordinata iz prostornih podataka
st_coordinates(pts_sfc_M)
# X Y
# [1,] 2279375.09936 5560872.97673
# koordinate treba zaokružiti do na cm
round(st_coordinates(pts_sfc_M),2)
# X Y
# [1,] 2279375.1 5560872.98
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import shapely.geometry
import geopandas as gpd
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = shapely.geometry.Point(20.4759749, 44.8057705)
# potom pravimo kolekciju geometrije sa koor. ref.sis
grf_geom_proj = gpd.GeoSeries([grf], crs=4326)
# prostorni lejer
grf_layer_proj = gpd.GeoDataFrame({'geometry': grf_geom_proj})
# transformacija u Merkatorovu projekciju
grf=grf_layer_proj.to_crs("+proj=merc +datum=WGS84")
print(grf)
# geometry
# 0 POINT (2279375.099 5560872.977)Primer 2: Računanje koordinata jedne tačke, srednji meridijan kao koordinatna osa
Za istu tačku sračunati pravougle koordinate kad je osa koordinatnog sistema postavljena da prolazi kroz srednji meridijan područja preslikavanja (Srbija) \(\lambda_0=21^o\).
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = st_point( c(20.4759749, 44.8057705) ) # lon , lat
# potom pravimo kolekciju geometrije sfc
pts_sfc = st_sfc(grf, crs=4326)
# epsg kod 4326 je +proj=longlat +datum=WGS84 +type=crs
# transformacija u Merkatorovu projekciju
pts_sfc_M = st_transform(pts_sfc, crs = "+proj=merc +lon_0=21 +datum=WGS84")
pts_sfc_M
# Geometry set for 1 feature
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -58334.2072949 ymin: 5560872.97673 xmax: -58334.2072949 ymax: 5560872.97673
# Projected CRS: +proj=merc +lon_0=21 +datum=WGS84
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# matrica koordinata iz prostornih podataka
st_coordinates(pts_sfc_M)
# X Y
# [1,] -58334.2072949 5560872.97673
# koordinate treba zaokružiti do na cm
round(st_coordinates(pts_sfc_M),2)
# X Y
# [1,] -58334.21 5560872.98
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import shapely.geometry
import geopandas as gpd
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = shapely.geometry.Point(20.4759749, 44.8057705)
# potom pravimo kolekciju geometrije sa koor. ref.sis
grf_geom_proj = gpd.GeoSeries([grf], crs=4326)
# prostorni lejer
grf_layer_proj = gpd.GeoDataFrame({'geometry': grf_geom_proj})
# transformacija u Merkatorovu projekciju
grf=grf_layer_proj.to_crs("+proj=merc +lon_0=21 +datum=WGS84")
print(grf)
# geometry
# 0 POINT (-58334.207 5560872.977)Kao što imamo slučaj kad je Grinič osa koordinatnog sistema da su sve koordinate u pravcu istoka (E, geodetski \(y\)) zapadno od Griniča negativne, tako i sad imamo slučaj da su sve koordinate u pravcu istoka negativne za \(\lambda<\lambda_0\), tj. za sve tačke zapadno od srednjeg meridijana područja. Da bi se izbegao rad sa negativnim koordinatama, često se definiše da početna koordinata koordinatnog sistema nije 0 nego neka unapred zadata vrednost.
Primer 3: Računanje koordinata jedne tačke, zadavanje početne vrednosti u pravcu istoka (false easting)
Sračunati koordinate za istu tačku kao u prethodnim primerima kada je zadata \(E_0\) (false easting) koordinata da iznosi 400.000 m.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = st_point( c(20.4759749, 44.8057705) ) # lon , lat
# potom pravimo kolekciju geometrije sfc
pts_sfc = st_sfc(grf, crs=4326)
# epsg kod 4326 je +proj=longlat +datum=WGS84 +type=crs
# transformacija u Merkatorovu projekciju
pts_sfc_M = st_transform(pts_sfc, crs = "+proj=merc +lon_0=21 +x_0=400000 +datum=WGS84")
pts_sfc_M
# Geometry set for 1 feature
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: 341665.792705 ymin: 5560872.97673 xmax: 341665.792705 ymax: 5560872.97673
# Projected CRS: +proj=merc +lon_0=21 +x_0=400000 +datum=WGS84
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# matrica koordinata iz prostornih podataka
st_coordinates(pts_sfc_M)
# X Y
# [1,] 341665.792705 5560872.97673
# koordinate treba zaokružiti do na cm
round(st_coordinates(pts_sfc_M),2)
# X Y
# [1,] 341665.79 5560872.98
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import shapely.geometry
import geopandas as gpd
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = shapely.geometry.Point(20.4759749, 44.8057705)
# potom pravimo kolekciju geometrije sa koor. ref.sis
grf_geom_proj = gpd.GeoSeries([grf], crs=4326)
# prostorni lejer
grf_layer_proj = gpd.GeoDataFrame({'geometry': grf_geom_proj})
# transformacija u Merkatorovu projekciju
grf=grf_layer_proj.to_crs("+proj=merc +lon_0=21 +x_0=400000 +datum=WGS84")
print(grf)
# geometry
# 0 POINT (341665.793 5560872.977)Primer 4: Računanje deformacija
Kao što je već više puta pomenuto, direktni zadatak obuhvata i računanje deformacionih parametara, a ne samo projekciju koordinata. Sračunati linearnu razmeru, linearnu deformaciju, razmer površina i deformaciju površina za tačku korišćenu u prethodnim primerima.
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# WGS84 a=6378137.0 rf=298.257223563
# 2 linearno nezavisna parametra WGS84 elipsoida
a=6378137.0
rf=298.257223563 # rf=1/f
# geodetksa širina tačke u radijanima
fi= 44.8057705 *pi/180
# funkcija za poluprečnik krivine prvog vertikala
N = function(fi, a=6377397.155 , rf=299.1528128 ){
# fi u radijanima
f = 1/rf
e = sqrt(2*f - f^2)
N = a / sqrt( 1- e^2 * (sin(fi))^2 )
return(N)
}
# linearna razmera
m=n=a/(N(fi)*cos(fi))
round(m,6)
# [1] 1.407269
# linearna deformacija
dc = m-1
round(dc,6)
# [1] 0.407269
# deformacija u m/km, koliko se deformiše 1 km
dc*1000
# [1] 407.269191238
paste("Dužina od 1 km sa elipsoida je u projekciji duža za",
round(dc*1000,1) ,"m na poziciji sa g. š. 44.8057705")
# [1] "Dužina od 1 km sa elipsoida je u projekciji duža za 407.3 m na poziciji sa g. š. 44.8057705"
# razmer površina
p=m^2
round(p,6)
# [1] 1.980407
# deformacija površina
dp= p-1
round(dp,6)
# [1] 0.980407
import math
# WGS84 a=6378137.0 rf=298.257223563
# 2 linearno nezavisna parametra WGS84 elipsoida
a = 6378137.0
rf = 298.257223563 # rf=1/f
# geodetska širina tačke u radijanima
fi = 44.8057705 * math.pi / 180
# funkcija za poluprečnik krivine prvog vertikala
def N(fi, a=6377397.155, rf=299.1528128):
f = 1 / rf
e = math.sqrt(2 * f - f ** 2)
N = a / math.sqrt(1 - e ** 2 * (math.sin(fi)) ** 2)
return N
# linearna razmera
m = n = a / (N(fi) * math.cos(fi))
print(round(m, 6))
# 1.407269
# linearna deformacija
dc = m - 1
print(round(dc, 6))
# 0.407269
# deformacija u m/km, koliko se deformiše 1 km
print(dc * 1000)
# 407.26919123811547
print("Dužina od 1 km sa elipsoida je u projekciji duža za",
round(dc * 1000, 1), "m na poziciji sa g. š. 44.8057705")
# Dužina od 1 km sa elipsoida je u projekciji duža za 407.3 m na poziciji sa g. š. 44.8057705
# razmer površina
p = m ** 2
print(round(p, 6))
# 1.980407
# deformacija površina
dp = p - 1
print(round(dp, 6))
# 0.980407Primer 5: Grafik deformacija u zavisnosti od geodetske širine
Napraviti grafik razmere površina u zavisnosti od geodetske širine u Merkatorovoj projekciji.
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# WGS84 a=6378137.0 rf=298.257223563
# 2 linearno nezavisna parametra WGS84 elipsoida
a=6378137.0
rf=298.257223563 # rf=1/f
# geodetksa širine tačaka od 0 do 80 N u radijanima
fi= seq(0,80,by=1) *pi/180
# funkcija za poluprečnik krivine prvog vertikala
N = function(fi, a=6378137.0 , rf=298.257223563 ){
# fi u radijanima
f = 1/rf
e = sqrt(2*f - f^2)
N = a / sqrt( 1- e^2 * (sin(fi))^2 )
return(N)
}
# linearna razmera
m=n=a/(N(fi)*cos(fi))
# razmer površina
p=m^2
plot(fi*180/pi,p, main = "Razmer površina u zavisnosti od geod. širine",
xlab = parse(text = "varphi"), ylab = "p",type = "l")
grid()
import numpy as np
import matplotlib.pyplot as plt
# WGS84 a=6378137.0 rf=298.257223563
# 2 linearno nezavisna parametra WGS84 elipsoida
a = 6378137.0
rf = 298.257223563 # rf=1/f
# geodetska širine tačaka od 0 do 80 N u radijanima
fi = np.arange(0, 81) * np.pi / 180
# funkcija za poluprečnik krivine prvog vertikala
def N(fi, a=6378137.0, rf=298.257223563):
# fi u radijanima
f = 1 / rf
e = np.sqrt(2 * f - f ** 2)
N = a / np.sqrt(1 - e ** 2 * (np.sin(fi)) ** 2)
return N
# linearna razmera
m = n = a / (N(fi) * np.cos(fi))
# razmer površina
p = m ** 2
plt.plot(fi * 180 / np.pi, p)
plt.title("Razmer površina u zavisnosti od geod. širine")
plt.xlabel(r"$\varphi$")
plt.ylabel("p")
plt.grid(True)
plt.show()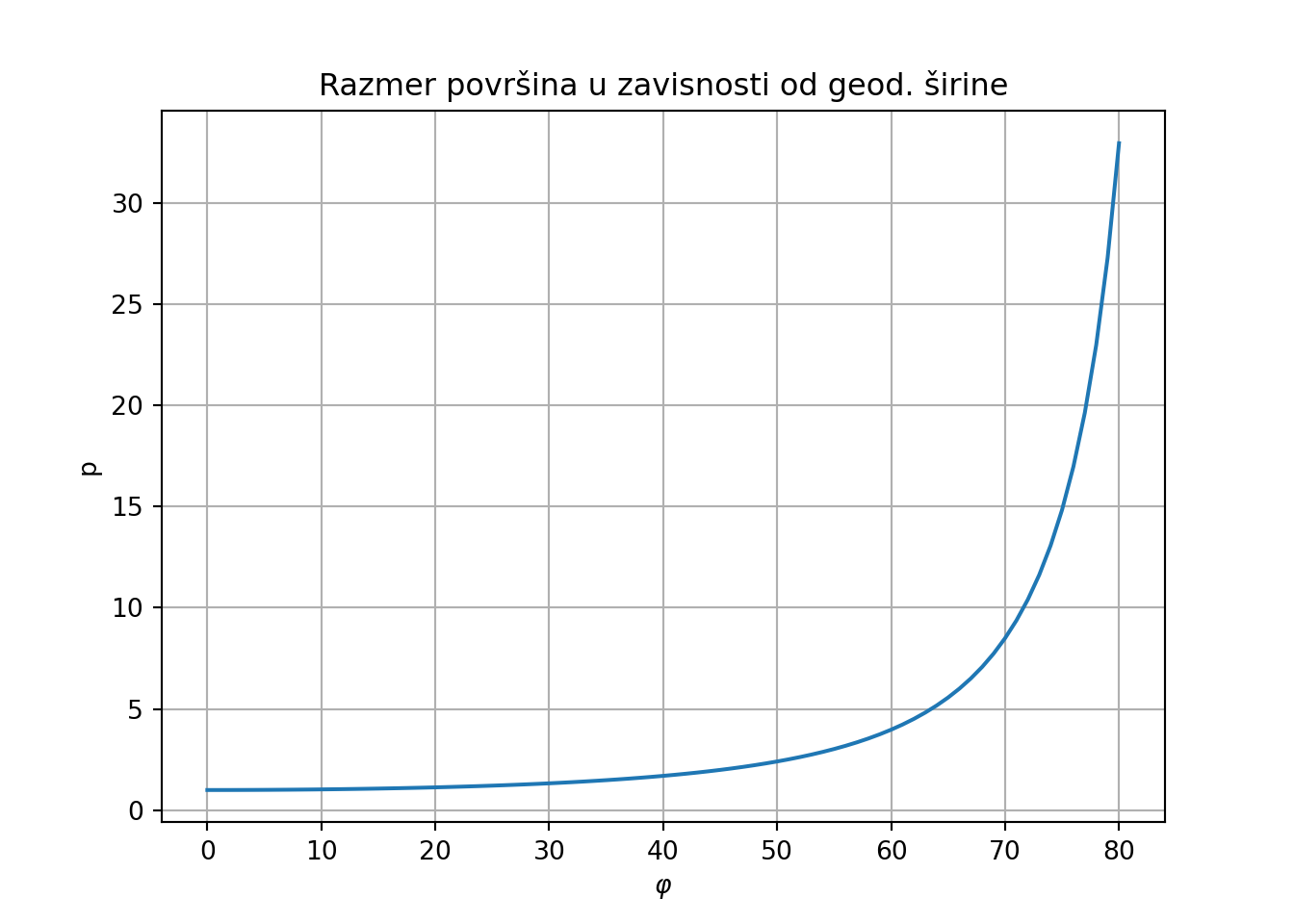
Vrlo je očigledno (Slika 4.11) da se dužine i površine veoma deformiši severnije od 60 stepeni geodetske širine kod Merkatorove projekcije.
Sledaća tabela (Tabela 4.1) pokazuje linearnu razmeru, linearnu deformaciju, razmer površina i deformaciju površina u zavisnosti od geodetske širine u Merkatorovoj projekciji.
options( digits = 12)
df =data.frame(Latituda = round(fi*180/pi ),
c = round(sqrt(p), 6),
dc= round(sqrt(p)-1 , 6),
p=round(p, 6),
dp =round(p-1 ,6) )
knitr::kable( df[seq(1,81,by=5), ],align = "c", row.names = FALSE,
format.args = list(scientific = FALSE, format = "f") ) | Latituda | c | dc | p | dp |
|---|---|---|---|---|
| 0 | 1.000000 | 0.000000 | 1.000000 | 0.000000 |
| 5 | 1.003794 | 0.003794 | 1.007603 | 0.007603 |
| 10 | 1.015324 | 0.015324 | 1.030883 | 0.030883 |
| 15 | 1.035044 | 0.035044 | 1.071316 | 0.071316 |
| 20 | 1.063761 | 0.063761 | 1.131587 | 0.131587 |
| 25 | 1.102718 | 0.102718 | 1.215987 | 0.215987 |
| 30 | 1.153734 | 0.153734 | 1.331102 | 0.331102 |
| 35 | 1.219430 | 0.219430 | 1.487008 | 0.487008 |
| 40 | 1.303601 | 0.303601 | 1.699375 | 0.699375 |
| 45 | 1.411845 | 0.411845 | 1.993306 | 0.993306 |
| 50 | 1.552665 | 0.552665 | 2.410769 | 1.410769 |
| 55 | 1.739527 | 0.739527 | 3.025953 | 2.025953 |
| 60 | 1.994973 | 0.994973 | 3.979917 | 2.979917 |
| 65 | 2.359687 | 1.359687 | 5.568123 | 4.568123 |
| 70 | 2.915150 | 1.915150 | 8.498099 | 7.498099 |
| 75 | 3.851618 | 2.851618 | 14.834963 | 13.834963 |
| 80 | 5.740046 | 4.740046 | 32.948123 | 31.948123 |
Primer 6: Transformacija vektorskih podataka i karta
Transformisati poligone opština u Srbiji u Merkatorovu projekciju. Poligoni opština se mogu preuzeti kroz WFS servis laboratorije za razvoj softvera otvorenog koda na Građevinskom fakultetu, OSGL Beograd.
library(sf)
# granice opština u Srb
url=paste('http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs',
'?service=WFS&version=1.0.0&',
'request=GetFeature&typeName=osgl_4:POP_age',sep='')
download.file(url, 'poage.gml')
pop = st_read('poage.gml')
# Reading layer `POP_age' from data source `C:\mk_knjiga\poage.gml' using driver `GML'
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# CRS: NA
st_crs(pop) = 4326
pop
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# Geodetic CRS: WGS 84
# First 10 features:
# gml_id ID_Municip NameASCII NameLatin Area SHAPE_Leng
# 1 POP_age.1 70335 Bosilegrad Bosilegrad 571273097 121715
# 2 POP_age.2 80195 Kanjiza Kanji�a 398623963 94729
# 3 POP_age.3 80438 Subotica Subotica 100734608 164832
# 4 POP_age.4 70572 Kladovo Kladovo 627254771 137660
# 5 POP_age.5 80454 Titel Titel 260745278 104386
# 6 POP_age.6 80110 Becej Becej 486479140 130561
# 7 POP_age.7 80268 Novi Becej Novi Becej 608393938 157111
# 8 POP_age.8 80136 Zabalj �abalj 399798048 127101
# 9 POP_age.9 80390 Srbobran Srbobran 284106212 89115
# 10 POP_age.10 80152 Zrenjanin Zrenjanin 132585270 272176
# SHAPE_Area NUTS0 NUTS1 NUTS2 NUTS3 TOTAL_POP ADULTS AVARAGE
# 1 5.71e+08 RS RS2 RS22 RS228 8129 6843 45.1774511
# 2 3.98e+08 RS RS1 RS12 RS124 25343 20842 42.44057531
# 3 1.01e+09 RS RS1 RS12 RS125 141554 116545 41.90601467
# 4 6.27e+08 RS RS2 RS22 RS221 20635 17644 46.75699055
# 5 2.61e+08 RS RS1 RS12 RS123 15738 12747 41.21559283
# 6 4.86e+08 RS RS1 RS12 RS123 37351 30217 41.47866188
# 7 6.08e+08 RS RS1 RS12 RS126 23925 19566 41.50948798
# 8 4.00e+08 RS RS1 RS12 RS123 26134 20616 39.71022423
# 9 2.84e+08 RS RS1 RS12 RS123 16317 13189 41.12824049
# 10 1.33e+09 RS RS1 RS12 RS126 123362 101780 42.19447642
# the_geom
# 1 MULTIPOLYGON (((22.3 42.6, ...
# 2 MULTIPOLYGON (((19.9 46.2, ...
# 3 MULTIPOLYGON (((19.7 46.2, ...
# 4 MULTIPOLYGON (((22.5 44.7, ...
# 5 MULTIPOLYGON (((20.2 45.3, ...
# 6 MULTIPOLYGON (((20.1 45.7, ...
# 7 MULTIPOLYGON (((20.3 45.8, ...
# 8 MULTIPOLYGON (((20.1 45.5, ...
# 9 MULTIPOLYGON (((20.1 45.5, ...
# 10 MULTIPOLYGON (((20.4 45.6, ...
pop = st_transform(pop, "+proj=merc +ellps=WGS84")
pop
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 2090000 ymin: 5110000 xmax: 2560000 ymax: 5780000
# Projected CRS: +proj=merc +ellps=WGS84
# First 10 features:
# gml_id ID_Municip NameASCII NameLatin Area SHAPE_Leng
# 1 POP_age.1 70335 Bosilegrad Bosilegrad 571273097 121715
# 2 POP_age.2 80195 Kanjiza Kanji�a 398623963 94729
# 3 POP_age.3 80438 Subotica Subotica 100734608 164832
# 4 POP_age.4 70572 Kladovo Kladovo 627254771 137660
# 5 POP_age.5 80454 Titel Titel 260745278 104386
# 6 POP_age.6 80110 Becej Becej 486479140 130561
# 7 POP_age.7 80268 Novi Becej Novi Becej 608393938 157111
# 8 POP_age.8 80136 Zabalj �abalj 399798048 127101
# 9 POP_age.9 80390 Srbobran Srbobran 284106212 89115
# 10 POP_age.10 80152 Zrenjanin Zrenjanin 132585270 272176
# SHAPE_Area NUTS0 NUTS1 NUTS2 NUTS3 TOTAL_POP ADULTS AVARAGE
# 1 5.71e+08 RS RS2 RS22 RS228 8129 6843 45.1774511
# 2 3.98e+08 RS RS1 RS12 RS124 25343 20842 42.44057531
# 3 1.01e+09 RS RS1 RS12 RS125 141554 116545 41.90601467
# 4 6.27e+08 RS RS2 RS22 RS221 20635 17644 46.75699055
# 5 2.61e+08 RS RS1 RS12 RS123 15738 12747 41.21559283
# 6 4.86e+08 RS RS1 RS12 RS123 37351 30217 41.47866188
# 7 6.08e+08 RS RS1 RS12 RS126 23925 19566 41.50948798
# 8 4.00e+08 RS RS1 RS12 RS123 26134 20616 39.71022423
# 9 2.84e+08 RS RS1 RS12 RS123 16317 13189 41.12824049
# 10 1.33e+09 RS RS1 RS12 RS126 123362 101780 42.19447642
# the_geom
# 1 MULTIPOLYGON (((2481361 522...
# 2 MULTIPOLYGON (((2220062 577...
# 3 MULTIPOLYGON (((2189608 577...
# 4 MULTIPOLYGON (((2501516 554...
# 5 MULTIPOLYGON (((2244923 564...
# 6 MULTIPOLYGON (((2233002 570...
# 7 MULTIPOLYGON (((2261325 571...
# 8 MULTIPOLYGON (((2237345 567...
# 9 MULTIPOLYGON (((2232410 567...
# 10 MULTIPOLYGON (((2268645 568...
# Karta opština u Merkatorovoj projekciji
plot(st_geometry(pop), graticule = TRUE, border = 'grey', axes = TRUE)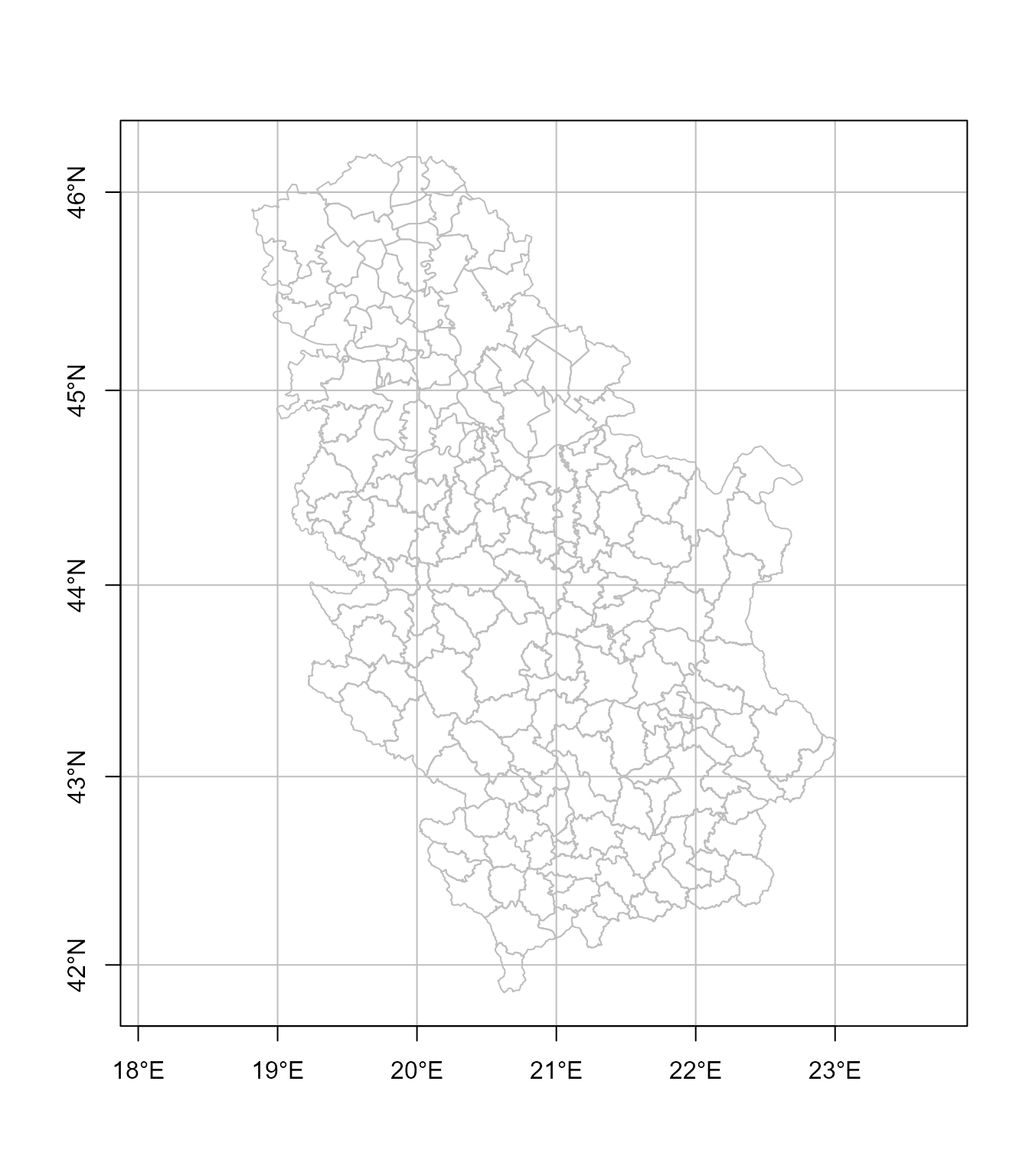
import geopandas as gpd
import matplotlib.pyplot as plt
import requests
# granice opština u Srb
url = 'http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs' + \
'?service=WFS&version=1.0.0&request=GetFeature&typeName=osgl_4:POP_age'
response = requests.get(url)
# snimamo fajl na disk
open('data/pop.gml', 'wb').write(response.content)
# 9461553
gdf = gpd.read_file('data/pop.gml')
# Podaci su u WGS84 (EPSG:4326)
gdf.crs = 'epsg:4326'
gdf
# gml_id ... geometry
# 0 POP_age.1 ... MULTIPOLYGON (((22.29045 42.59307, 22.29047 42...
# 1 POP_age.2 ... MULTIPOLYGON (((19.94315 46.17601, 19.94470 46...
# 2 POP_age.3 ... MULTIPOLYGON (((19.66958 46.18402, 19.66976 46...
# 3 POP_age.4 ... MULTIPOLYGON (((22.47150 44.71333, 22.47564 44...
# 4 POP_age.5 ... MULTIPOLYGON (((20.16648 45.32598, 20.16532 45...
# .. ... ... ...
# 192 POP_age.193 ... MULTIPOLYGON (((21.28057 42.44932, 21.28637 42...
# 193 POP_age.194 ... MULTIPOLYGON (((21.56451 42.73154, 21.56464 42...
# 194 POP_age.195 ... MULTIPOLYGON (((21.46112 42.62940, 21.46216 42...
# 195 POP_age.196 ... MULTIPOLYGON (((20.59400 42.88168, 20.60346 42...
# 196 POP_age.197 ... MULTIPOLYGON (((19.54257 44.48493, 19.54272 44...
#
# [197 rows x 15 columns]
# transformišemo u Merkatorovu projekciju
# epsg kod 3395 je
# +proj=merc +lon_0=0 +k=1 +x_0=0 +y_0=0 +datum=WGS84 +units=m +type=crs
gdf = gdf.to_crs(epsg=3395)
gdf
# gml_id ... geometry
# 0 POP_age.1 ... MULTIPOLYGON (((2481361.202 5221309.745, 24813...
# 1 POP_age.2 ... MULTIPOLYGON (((2220061.513 5777759.770, 22202...
# 2 POP_age.3 ... MULTIPOLYGON (((2189607.922 5779043.319, 21896...
# 3 POP_age.4 ... MULTIPOLYGON (((2501515.678 5546430.059, 25019...
# 4 POP_age.5 ... MULTIPOLYGON (((2244922.631 5642589.951, 22447...
# .. ... ... ...
# 192 POP_age.193 ... MULTIPOLYGON (((2368941.892 5199677.410, 23695...
# 193 POP_age.194 ... MULTIPOLYGON (((2400550.029 5242194.756, 24005...
# 194 POP_age.195 ... MULTIPOLYGON (((2389041.008 5226784.944, 23891...
# 195 POP_age.196 ... MULTIPOLYGON (((2292514.098 5264895.003, 22935...
# 196 POP_age.197 ... MULTIPOLYGON (((2175468.466 5510843.331, 21754...
#
# [197 rows x 15 columns]
# Karta
ax = gdf.plot(edgecolor='grey', figsize=(10, 8))
ax.set_axis_on()
ax.set_xlabel('E')
ax.set_ylabel('N')
plt.grid(True)
plt.show()
Primer 7: Loksodroma u Merkatorovoj projekciji
U poglavlju Referentne površi i koordinatni referentni sistemi 2.4.10 smo sračunali da dužina loksodrome od Beograda (\(\varphi=44.800153\) i \(\lambda=20.455727\)) do Tokija (\(\varphi=35.679207\) i \(\lambda=139.767118\)) iznosi 10163304 m (10163 km). Sračunati dužinu loksodrome u Merkatorovoj projekciji.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# geometrija bg, tk
bg = st_point( c(20.455727, 44.800153) ) # lon , lat
tk = st_point( c(139.767118, 35.679207) ) # lon , lat
# potom pravimo kolekciju geometrije sfc
pts_sfc = st_sfc(c(bg,tk), crs=4326)
# epsg kod 4326 je +proj=longlat +datum=WGS84 +type=crs
# transformacija u Merkatorovu projekciju
pts_sfc_M = st_transform(pts_sfc, crs = "+proj=merc +datum=WGS84")
pts_sfc_M
# Geometry set for 1 feature
# Geometry type: MULTIPOINT
# Dimension: XY
# Bounding box: xmin: 2277121.11345 ymin: 4231647.85989 xmax: 15558804.4054 ymax: 5559994.62218
# Projected CRS: +proj=merc +datum=WGS84
# matrica koordinata iz prostornih podataka
EN=st_coordinates(pts_sfc_M)
# loksodroma je prava linija u Merkatorovoj projekciji
# računamo dužinu iz koordinata
Dl = sqrt(diff(EN[,1])^2 +diff(EN[,2])^2)
# dužina u m
round(Dl)
# [1] 13347944
# dužina u km
round(Dl/1000)
# [1] 13348
# a dužina na elispoidu je 10163 km
import shapely.geometry
import geopandas as gpd
# pravimo GeoDataFrame bg, tk
bg = shapely.geometry.Point( 20.455727, 44.800153) # lon , lat
tk = shapely.geometry.Point( 139.767118, 35.679207) # lon , lat
data = {'geometry': [bg, tk]}
bgtk = gpd.GeoDataFrame(data, crs="+proj=longlat +datum=WGS84")
# Merkatorova proj. preslikavanje sa WGS84 (EPSG:3395)
# transformacija u Merkatorovu projekciju
bgtk = bgtk.to_crs("+proj=merc +datum=WGS84")
print(bgtk)
# geometry
# 0 POINT (2277121.113 5559994.622)
# 1 POINT (15558804.405 4231647.860)
# Prikaz koordinata na 6 decimala
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
E = bgtk["geometry"].x
N = bgtk["geometry"].y
# računamo dužinu iz koordinata
Dl = ((E[1]-E[0])**2 +(N[1]-N[0])**2)**0.5
# dužina u m
print( round(Dl) )
# 13347944
# dužina u km
print( round(Dl/1000) )
# 13348
# a dužina na elispoidu je 10163 kmPrimer 8: Primer inverznog zadatka kod Merkatorove projekcije
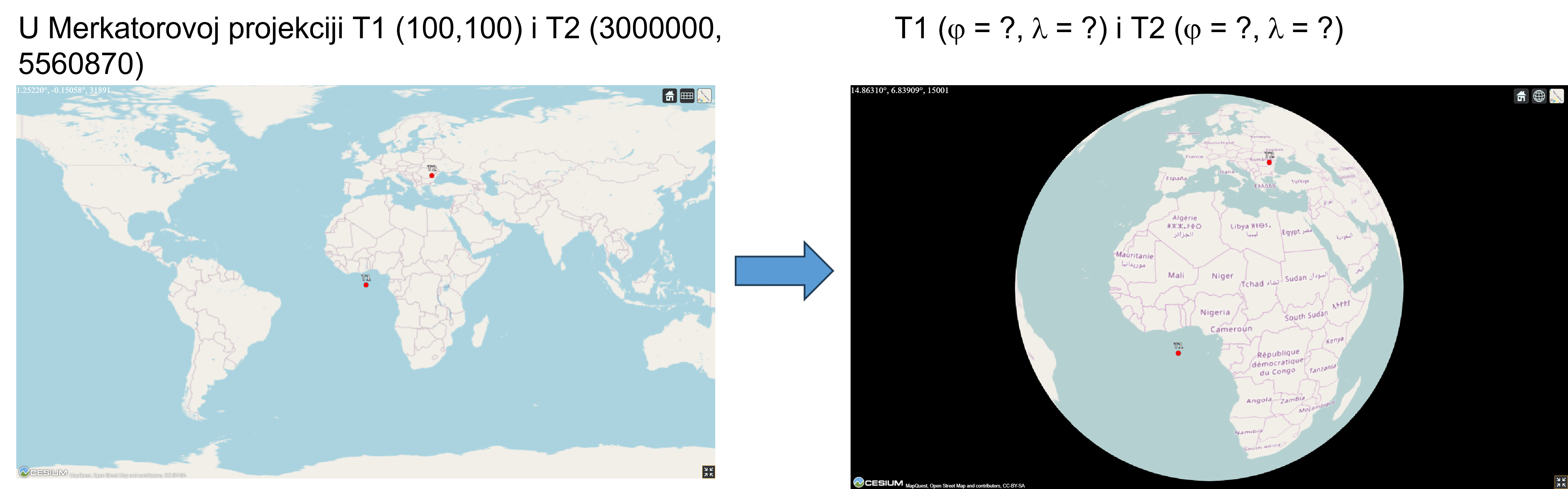
Pravougle Merkatorove koordinate T1(100, 100) i T2(3000000, 5560870) transformisati na elipsoidne u WGS84, Slika 4.14. Elipsoidne koordinate izraziti i u obliku stepen, minut i sekund.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Za tacke sa koordinatama 100, 100 i 3000000, 5560870 u Merkatorovoj projekciji
# Sračunaj koordinate na WGS84 elipsoidu
tM= st_sfc( st_point(c(100,100)), st_point(c(3000000, 5560870)),
crs = "+proj=merc +lon_0=0 +x_0=0 +y_0=0 +ellps=WGS84 +units=m" )
# inverzni zadatak iz pravouglih u longitudu, latitudu
tLL = st_transform(tM,
crs = "+proj=longlat +datum=WGS84 +no_defs") #ili 4326
ll = st_coordinates(tLL)
# Koordinate treba zaokružiti do na cm ili dm, što je oko 6. decimale
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
round(ll,6)
# X Y
# [1,] 0.000898 0.000904
# [2,] 26.949459 44.805751
# gedetska dužina i širina
# lon lat
lon = ll[,1]
lat = ll[,2]
# funkcija za stepen u stepen minut sekund
deg2dms <- function(deg){
deg_sign = sign(deg)
deg = abs(deg)
DEG = floor(deg)
MIN = floor((deg - DEG) * 60)
SEC = (deg - DEG - MIN/60) * 3600
SEC=round(SEC,2)
dms=paste(deg_sign*DEG,'\u00B0',MIN,"'",SEC,"''",sep='')
return(dms)
}
# gedetska dužina i širina
print(paste("T1 " ,deg2dms(lon[1]), deg2dms(lat[1])) )
# [1] "T1 0°0'3.23'' 0°0'3.26''"
print(paste( "T2 " ,deg2dms(lon[2]), deg2dms(lat[2])) )
# [1] "T2 26°56'58.05'' 44°48'20.71''"import shapely.geometry
import geopandas as gpd
# pravimo GeoDataFrame koordinate u Merkatorovoj projekciji
data = {'geometry': [shapely.geometry.Point(100, 100), shapely.geometry.Point(3000000, 5560870)]}
mer = "+proj=merc +lon_0=0 +x_0=0 +y_0=0 +ellps=WGS84 +units=m"
gdf = gpd.GeoDataFrame(data, crs= mer) # Merkatorova proj (EPSG:3395)
# transformacija u WGS84
gdf_wgs84 = gdf.to_crs("EPSG:4326")
print(gdf_wgs84)
# geometry
# 0 POINT (0.00090 0.00090)
# 1 POINT (26.94946 44.80575)
# Prikaz koordinata na 6 decimala
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
lon = gdf_wgs84["geometry"].x
lat = gdf_wgs84["geometry"].y
# gedetska dužina i širina
print("T1 " ,round(lon[0],6), round(lat[0],6))
# T1 0.000898 0.000904
print("T2 " ,round(lon[1],6), round(lat[1],6))
# T2 26.949459 44.805751
# funkcija za stepen u stepen minut sekund
def deg2dms(deg):
deg_sign = 1 if deg >= 0 else -1
deg = abs(deg)
DEG = int(deg)
MIN = int((deg - DEG) * 60)
SEC = (deg - DEG - MIN / 60) * 3600
SEC = round(SEC, 2)
dms = f"{deg_sign*DEG}\u00B0{MIN}'{SEC}''"
return dms
# gedetska dužina i širina
print(f"T1 {deg2dms(lon[0])} {deg2dms(lat[0])}")
# T1 0°0'3.23'' 0°0'3.26''
print(f"T2 {deg2dms(lon[1])} {deg2dms(lat[1])}")
# T2 26°56'58.05'' 44°48'20.71''
Bugayevskiy, Lev M, and John Snyder. 2013. Map Projections: A Reference Manual. CRC Press.
Jovanović, Velibor. 1984. Matematička Kartografija. VGI.
Kessler, Fritz C, Sarah E Battersby, Michael P Finn, and Keith C Clarke. 2017. “Map Projections and the Internet.” Choosing a Map Projection, 117–48.
Kilibarda, Milan, and Dragutin Protić. 2018. Geovizualizacija i Web Kartografija. Univerzitet u Beogradu, Građevinski fakultet. http://osgl.grf.bg.ac.rs/books/gvvk/index.html.
Krakiwsky, Edward J. 1973. Conformal Map Projections in Geodesy. 37. Department of Surveying Engineering. University of New Brunswick.
Lapaine, Miljenko, and E Lynn Usery. 2017. Choosing a Map Projection. Springer.
Peterson, Michael P. 2012. Online Maps with APIs and WebServices. Springer Science & Business Media.
Snyder, John Parr. 1987. Map Projections–a Working Manual. Vol. 1395. US Government Printing Office.