2  Referentne površi i koordinatni referentni sistemi

Precizno definisanje lokacija je od suštinskog značaja za dalje razumevenje matematičke kartografije. Ovo poglavlje pretstavlja ukorenjene koncepte geodetskih koordinata i njihovu primenu u različitim koordinatnim referentnim sistemima. U prethodnom poglavlju smo videli da se planeta Zemlja najčešće aproksimira referentnim površima i da se za aproksimaciju koriste: geoid, elipsoid, sfera i ravan. Kroz sledeće sekcije, razmotrićemo različite kocepte koordinata: u ravni, na sferi i elipsoidu, pravougle, polarne, krivolinijske, kao i njihovu konverziju iz jednog oblika u drugi. Pored toga opisana su računanja u ravni, na sferi i elipsoidu za one elemente koja su neophodna za buduća poglavlja koja slede i koja opisuju konkretne kartografske projekcije. Takođe, predstavljen je koncept geodetskog koordinatnog referentnog sistema i koordinatnog referentnog sistema u projekciji. Osim toga, upoznaćemo se sa PROJ (PROJ contributors 2023) bibliotekom, moćnim alatom za koordinatna računanja, i WKT-2 (Lott 2015) formatom za opis koordinatnih referentnih sistema. Kroz praktične primere ilustrovaćemo kako se računanja na elipsoidu obavljaju pomoću sf (Pebesma 2018a) i s2 (Dunnington, Pebesma, and Rubak 2023) R paketa.

2.1 Koordinate

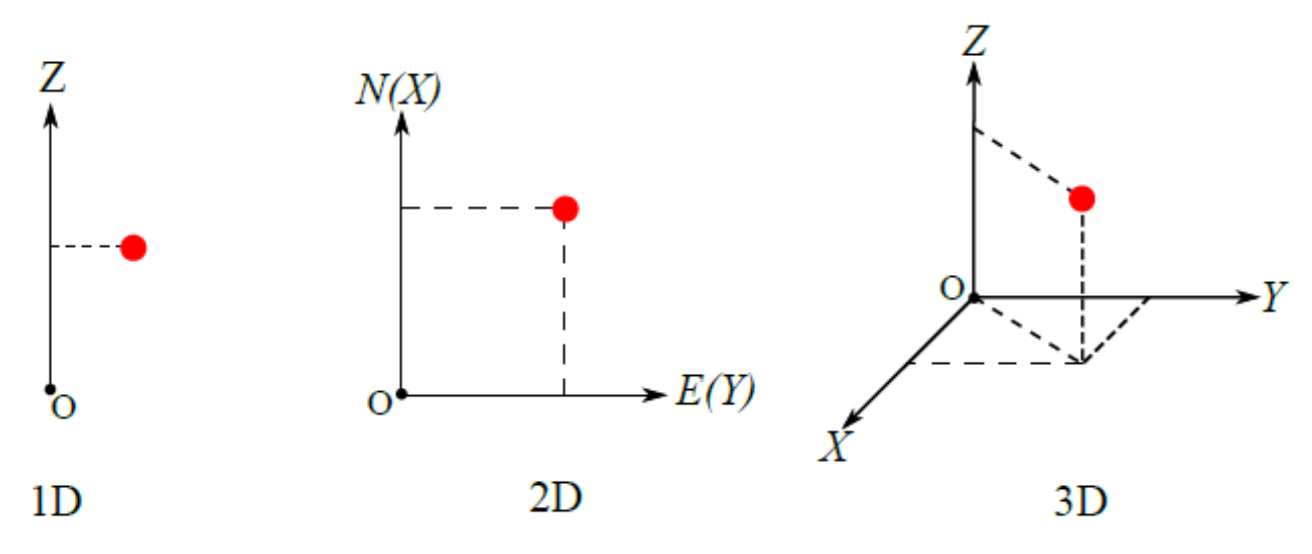
Koordinate (lat. co: zajedno i ordinatus: uređeni, definisani) su brojevi čijim se zadavanjem opisuje položaj tačaka u ravni, pravcu ili uopšteno u prostoru. Koordinata mora imati definisanu jedinicu (meru) i ishodište (koordinatni početak). Koordinatni sistemi su najčešće jednodimenzioni, dvodimenzioni ili trodimenzioni, Slika 2.1. U geodeziji je usvojeno da koordinata u pravcu severa ima oznaku \(X\) (ili \(x\)), a u pravcu istoka \(Y\) (ili \(y\)). To je zbog analogije da se obično tačka na elipsoidu zadaje redosledom geodetska širina pa geodetska dužina.

Slika 2.1: Koordinate u 1D, 2D i 3D prostoru, (Varga 2021).

2.2 Koordinatne u ravni

Kao što je već rečeno u prethodnom poglavlju (Poglavlje 1), u kartografiji često kooristimo koordinate u ravni. Kad se koriste kartografske projekcije deo planete ili cela planeta može se predstaviti njenom projekcijom u ravni karte. Ravan možemo parametrizovati parametarskim ili koordninatnim linijama. Parametarske linije u ravni odlikuju se time što duž svake od njih parametar ima odgovarajuću konstantnu vrednost (xi=const ili yi=const) koja se menja pri prelazu na drugu liniju istog sistema.

Vrednosti parametara nazivaju se koordinatama, a parametarske linije koordinatnim linijama. Mreža koordinatnih linija postavljenih na konstantnim razmacima (dx=const i dz=const) zamišljeno pokriva celu ravan i deli je na bezbroj malih kvadrata ili na konačan broj, Slika 2.2. Na katastarskim planovima uobičajeno je da su koordinatne linije materijalizovane decimetarskom mrežom.

Code 
E = c(7500000, 7500100)
N = c(4900000,4900100)
plot(E, N, asp=1, xlim = c(7500000, 7500110), ylim=c(c(4900000,4900110)))
grid( lty = 2, col = "gray", lwd = 2)

Slika 2.2: Koordinatne linije u ravni.
Code 
import matplotlib.pyplot as plt

E = [7500000, 7500100]
N = [4900000, 4900100]

plt.plot(E, N,  'o')
plt.gca().set_aspect('equal')
plt.xlim([7500000-10, 7500110])
# (7499990.0, 7500110.0)
plt.ylim([4900000-10, 4900110])
# (4899990.0, 4900110.0)
plt.grid(linestyle='dashed', color='gray', linewidth=2)
plt.show()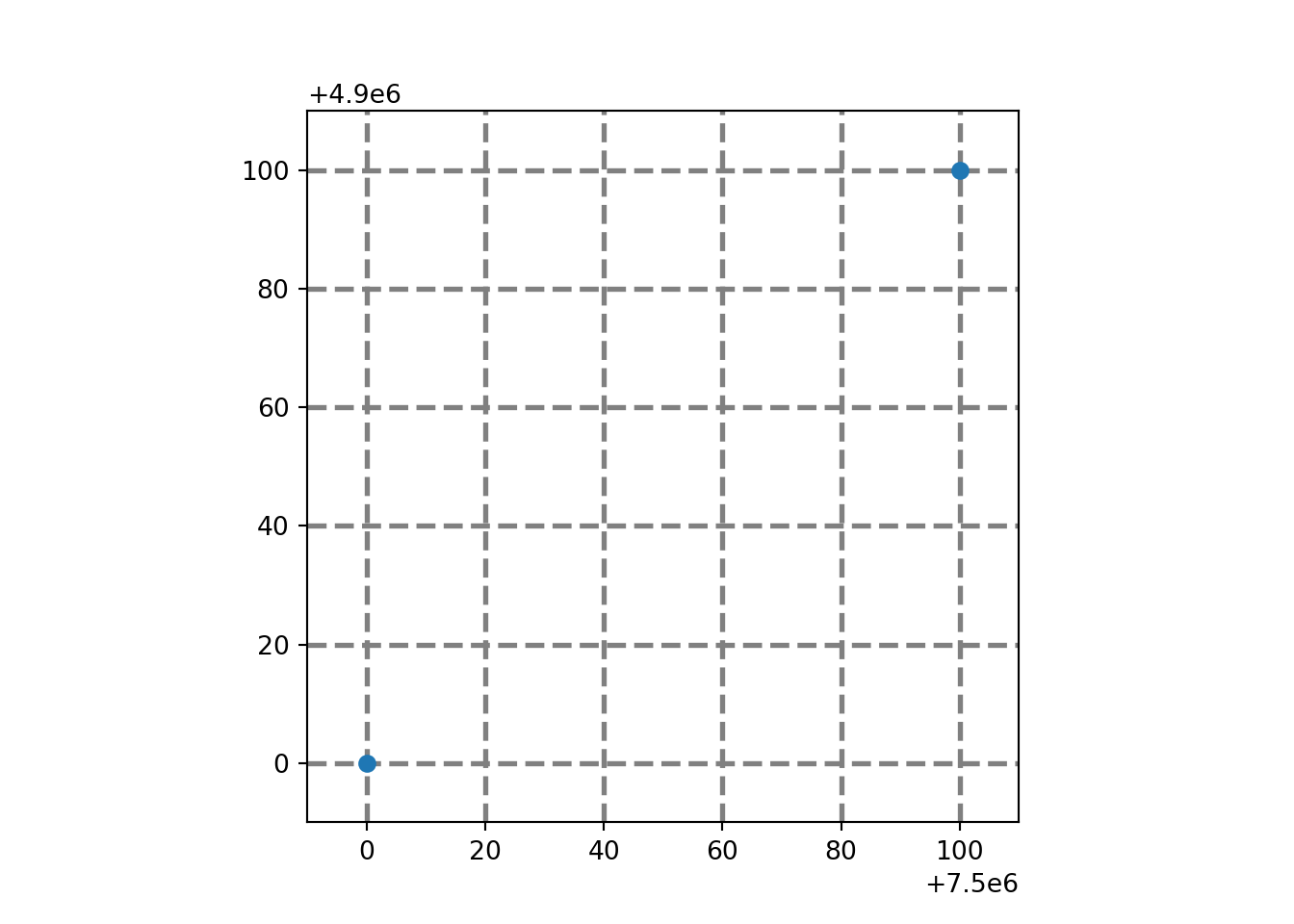

Koordinatne linije u ravni.

Razlike koordinata dobiju se izrazima, Slika 2.3:

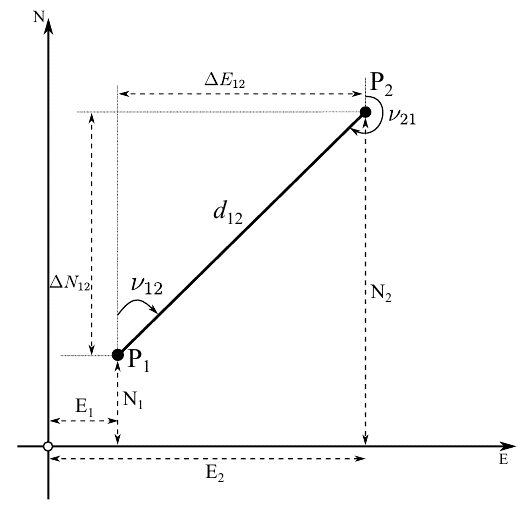
Slika 2.3: Direkcioni ugao, (Varga 2021).

\[ \begin{aligned} & \Delta \mathrm{E}_{2-1}=\mathrm{E}_2-\mathrm{E}_1=\mathrm{d}_{1-2} \sin \left(\mathrm{\nu}_{1-2}\right) \\ & \Delta \mathrm{N}_{2-1}=\mathrm{N}_2-\mathrm{N}_1=\mathrm{d}_{1-2} \cos \left(\mathrm{\nu}_{1-2}\right) \end{aligned} \]

Direkcioni uglovi (azimut u ravni) definisani su u smeru kazaljke na satu od severne ose.

\[ \nu_{1-2}=\nu_{2-1} \pm 180^{\circ} \]

Rastojanje između dve tačke u ravni računa se koristeći formulu:

\[ d_{12} = \sqrt{(E_2-E_1)^2+(N_2-N_1)^2} \]

Slika 2.4 prikazuje kako se računa direkcioni ugao u zavisnosti od toga koji je predznak razlike koordinata po horizontalnoj i vertikalnoj osi.

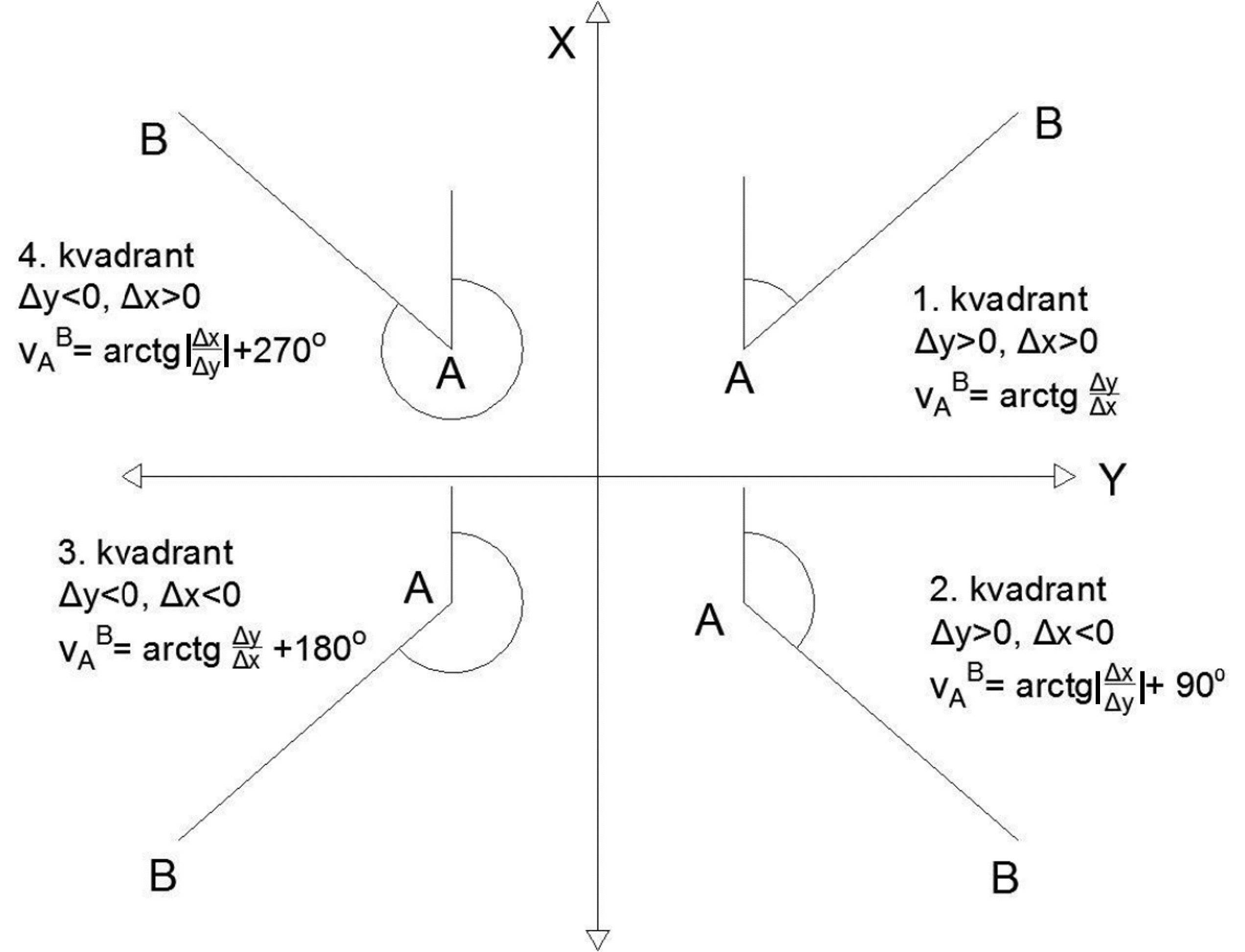
Slika 2.4: Direkcioni ugao, računanje.

Formula za direkcioni ugao data je sledećim izrazom:

\[ \operatorname{direkcioni}(\Delta E, \Delta N) = \begin{cases} \arctan\left(\frac {\Delta E} {\Delta N}\right) &\text{ako je } {\Delta N} > 0 \text{ i } {\Delta E} > 0, \\[5mu] \arctan\left (|\frac {\Delta N} {\Delta E}\right |) +\frac{\pi}{2} &\text{ako je } {\Delta N} < 0 \text{ i } {\Delta E} > 0, \\[5mu] \arctan\left (\frac {\Delta E} {\Delta N}\right ) +\pi &\text{ako je } {\Delta N} < 0 \text{ i } {\Delta E} < 0, \\[5mu] \arctan\left (|\frac {\Delta N} {\Delta E}\right |) +\frac{3\pi}{2} &\text{ako je } {\Delta N} > 0 \text{ i } {\Delta E} < 0, \\[5mu] \end{cases} \]

Formula za direkcioni ugao ako koristimo geodetske oznake koordinata:

\[ \operatorname{direkcioni}(\Delta Y, \Delta X) = \begin{cases} \arctan\left(\frac {\Delta Y} {\Delta X}\right) &\text{ako je } {\Delta X} > 0 \text{ i } {\Delta Y} > 0, \\[5mu] \arctan\left (|\frac {\Delta X} {\Delta Y}\right |) +\frac{\pi}{2} &\text{ako je } {\Delta X} < 0 \text{ i } {\Delta Y} > 0, \\[5mu] \arctan\left (\frac {\Delta Y} {\Delta X}\right ) +\pi &\text{ako je } {\Delta X} < 0 \text{ i } {\Delta Y} < 0, \\[5mu] \arctan\left (|\frac {\Delta X} {\Delta Y}\right |) +\frac{3\pi}{2} &\text{ako je } {\Delta X} > 0 \text{ i } {\Delta Y} < 0, \\[5mu] \end{cases} \]

Sledeći kod daje primer računanja direkcionog ugla. Prvo je kreirana funkcija za računanje direkcionog ugla, a potom on sračunat pozivom funkcije.

direkcioni <- function(YA, XA, YB, XB, jedinice = "rad") {
  # Ovo je funkcija koja računa direkcioni iz koordinata za dve zadate tačke
  # YA (EA) koordinta u pravcu istoka za tačku A
  # XA (NA) koordinta u pravcu severa  za tačku A
  # YB (EB) koordinta u pravcu istoka za tačku B
  # XB (NB) koordinta u pravcu severa  za tačku B
  # opcija jedinice može biti "rad" ili "st"
    
  dx <- XB - XA
  dy <- YB - YA
  
  if (dx > 0 && dy > 0) {
    dir <- atan(dy / dx)  # kv = 1
  } else if (dy > 0 && dx < 0) {
    dir <- atan(abs(dx / dy)) + pi/2  # kv = 2
  }else if (dy < 0 && dx < 0) {
    dir <- atan(abs(dx / dy)) + pi # kv = 3
  }else {
    dir <- atan(abs(dx / dy)) + pi*3/2  # kv = 4
  }
  
  if (jedinice != "rad") {
    dir <- 180/pi * dir
  }
  
  return(dir)
}

# Poziv funkcije
dab <- direkcioni(7500000, 4900000, 7500100, 4900100, "st")
print(dab)
# [1] 45
# test
direkcioni(0, 0, 1,1, "st")==45
# [1] TRUE
direkcioni(0, 0, 1,-1, "st")==135
# [1] TRUE
direkcioni(0, 0, -1,-1, "st")==225
# [1] TRUE
direkcioni(0, 0, -1,1, "st")==315
# [1] TRUE
def direkcioni(YA,XA,YB,XB, jedinice="rad"):
    """
    Ovo je funkcija koja računa direkcioni iz koordinata za dve zadate tačke
    YA (EA) koordinta u pravcu istoka za tačku A
    XA (NA) koordinta u pravcu severa  za tačku A
    YB (EB) koordinta u pravcu istoka za tačku B
    XB (NB) koordinta u pravcu severa  za tačku B
    opcija jedinice može biti "rad" ili "st"
    """
    
    import math
    # funkcija za arkus tangens je math.atan
    atan = math.atan
 
    dx = XB-XA
    dy = YB - YA

    if dx>0 and dy>0:
        dir = atan(dy/dx) #        kv = 1
    elif dy>0 and dx<0 :
        dir = atan(abs(dx/dy)) + math.pi/2  #   kv = 2
    elif dy<0 and dx<0 :
        dir = atan(dx/dy) + math.pi #         kv = 3
    else:
        dir = atan(abs(dx/dy)) + math.pi*3/2 # kv = 4
             
    if(jedinice != "rad"): dir= 180/math.pi *dir
    return dir


### Poziv funkcije
dab = direkcioni(7500000,4900000,7500100,4900100,"st")
print(dab)
# 45.0

# test
direkcioni(0, 0, 1,1, "st")==45
# True
direkcioni(0, 0, 1,-1, "st")==135
# True
direkcioni(0, 0, -1,-1, "st")==225
# True
direkcioni(0, 0, -1,1, "st")==315
# True

Polarne koordinate u ravni mogu se zadati sa dva parametra, radijus vektorom i uglom koji taj vektor zaklapa sa horizontalnom osom \(\psi\).

Code 
# Edzer Pebesma https://r-spatial.org/book

par(mar = rep(0,4))
plot(3, 4, xlim = c(-6,6), ylim = c(-6,6), asp = 1)
axis(1, pos = 0, at = 0:6)
axis(2, pos = 0, at = -6:6)
xd <- seq(-5, 5, by = .1)
lines(xd, sqrt(25 - xd^2), col = 'grey')
lines(xd, -sqrt(25 - xd^2), col = 'grey')
arrows(0, 0, 3, 4, col = 'red', length = .15, angle = 20)
text(1.5, 2.7, label = parse(text = "rho"), col = 'red')
xd <- seq(3/5, 1, by = .1)
lines(xd, sqrt(1 - xd^2), col = 'red')
text(1.2, 0.5, label = parse(text = "psi"), col = 'red')
lines(c(3,3), c(0,4), lty = 2, col = 'blue')
lines(c(0,3), c(4,4), lty = 2, col = 'blue')
text(3.3, 2.5, label = "N", col = 'blue')
text(1.5, 4.3, label = "E", col = 'blue')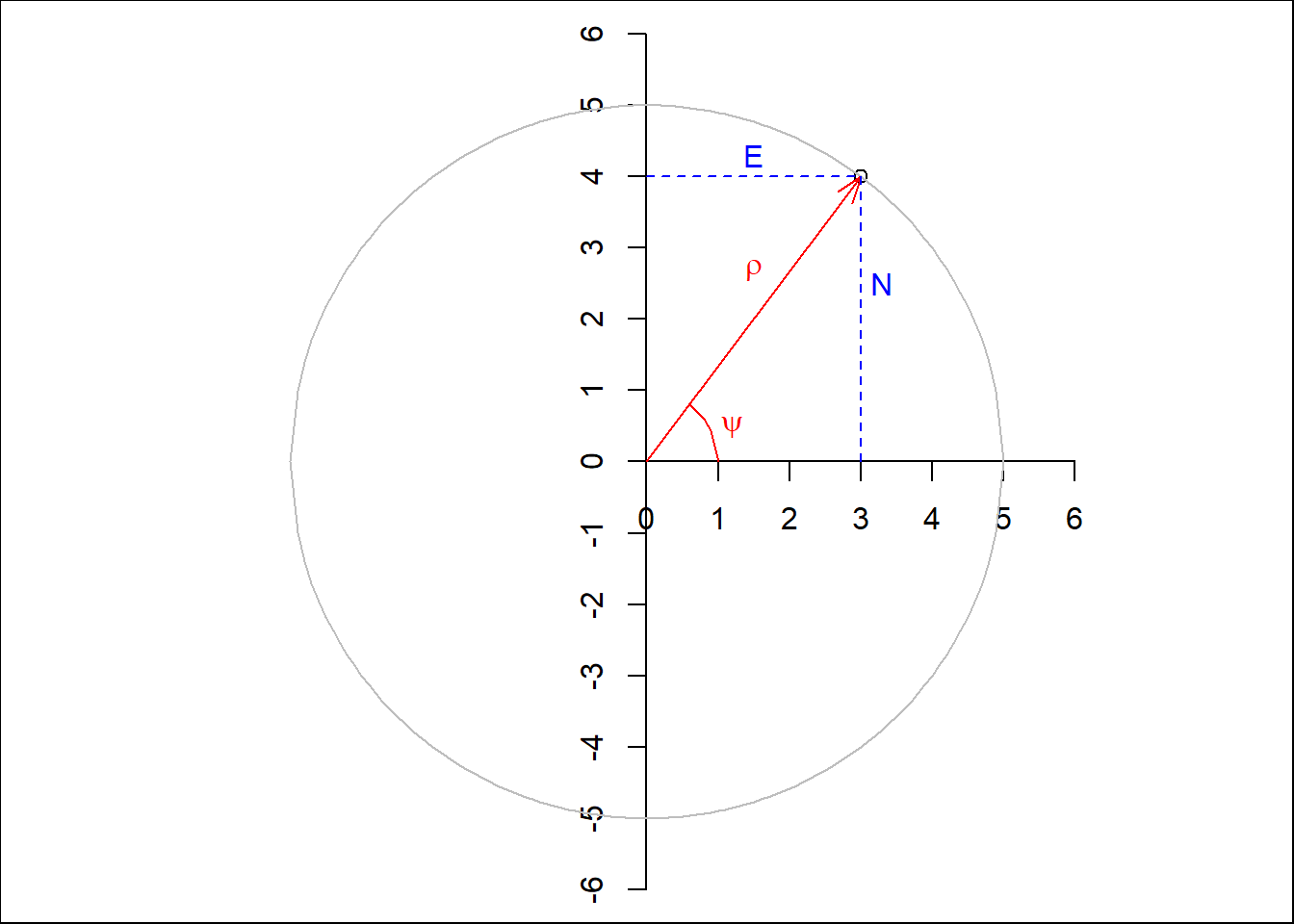

Slika 2.5: Odnos polarnih i pravouglih koordinata u ravni

Slika 2.5 pokazuje odnos polarnih i pravouglih koordinata u ravni. Tačka sa koordinatama \((E,N) = (3,4)\) je \((\rho,\psi) = (5, \mbox{arctan}(4/3))\), gde je \(\mbox{arctan}(4/3)\) oko \(53^{\circ}\). Jednostavan je odnos ova dva sistema koordinata u ravni.

\[E = \rho~\mbox{cos} \psi,\ \ \ N = \rho~\mbox{sin} \psi, \ \mbox{i}\] \[\rho = \sqrt{E^2 + N^2}, \ \ \ \psi = \mbox{atan2}(N, E)\] Funkcija \(\mbox{atan2}\) uzima u obzir kvadrante u odnosu na horizontalnu osu.

\[ \operatorname{atan2}(N, E) = \begin{cases} \arctan\left(\frac N E\right) &\text{ako je } E > 0, \\[5mu] \arctan\left(\frac N E\right) + \pi &\text{ako je } E < 0 \text{ i } N \ge 0, \\[5mu] \arctan\left(\frac N E\right) - \pi &\text{ako je } E < 0 \text{ i } N < 0, \\[5mu] +\frac{\pi}{2} &\text{ako je } E = 0 \text{ i } N > 0, \\[5mu] -\frac{\pi}{2} &\text{ako je } E = 0 \text{ i } N < 0, \\[5mu] \text{nedefinisano} &\text{ako je } E = 0 \text{ i } N = 0. \end{cases} \]

2.3 Koordinate na sferi

Kad se planeta Zemlja aproksimira sferom (loptom) koja je referentna površ (veće složenosti nego ravan, ali se zanemaruje činjenica da je Zemlja spljoštena na polovima i da je bolja aproksimacija elipsoid, (videti Slika 1.30), podrazumeva se da se centar sfere poklapa sa centrom mase Zemlje. Poluprečnik koji prolazi kroz usvojenu poziciju Severnog i Južnog pola naziva se obrtna osa lopte ili sfere, obrtna osa je prečnik PNPS, (Slika 2.6).

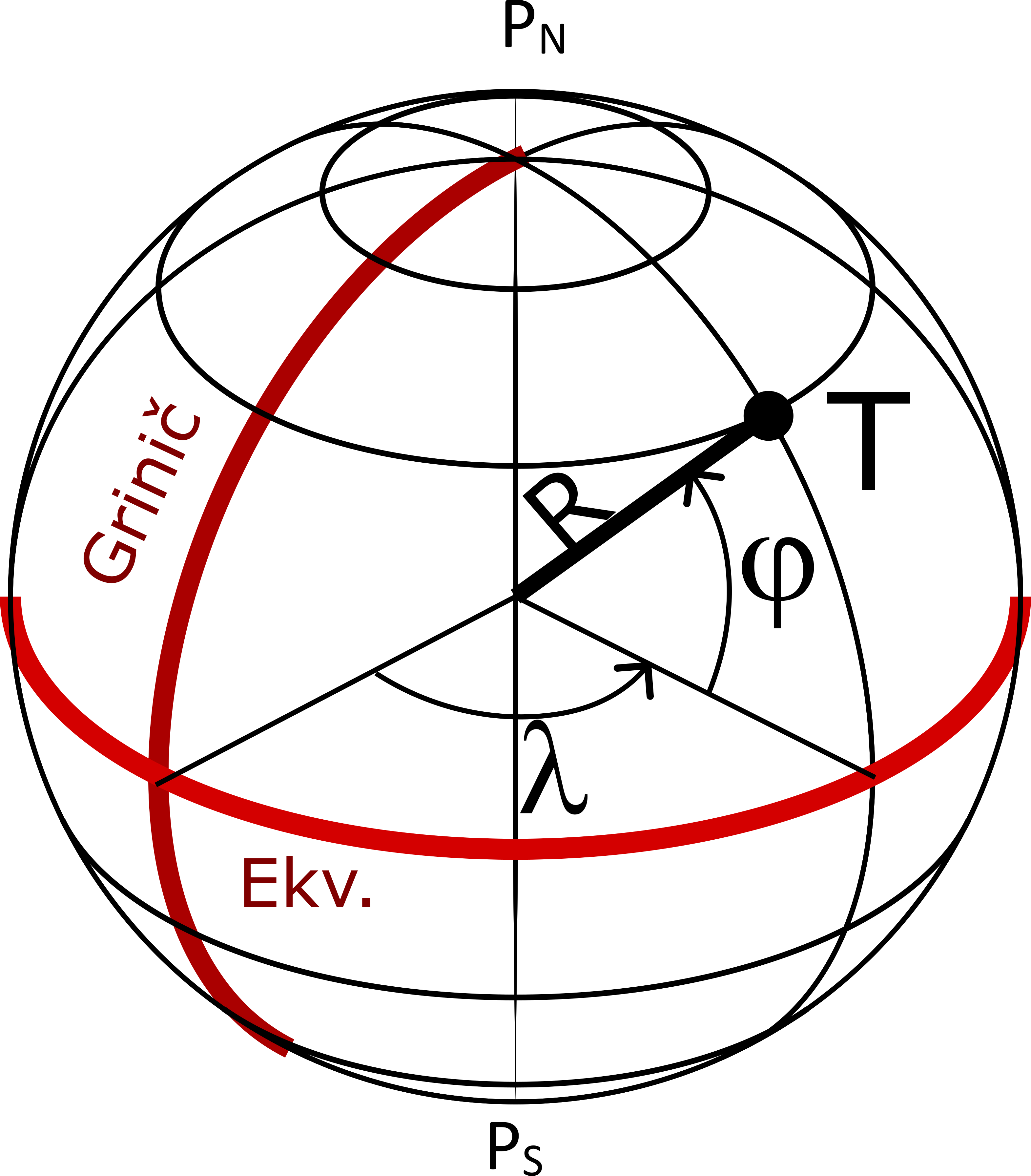
Slika 2.6: Aproksimacija Zemlje koristeći sferu (loptu).
Meridijani i paralele

Karakteristične tačke, linije i ravni Zemljine lopte dobijaju se njenim presecanjem sa ravnima postavljenim kroz obrtnu osu (meridijanske ravni), ili sa ravnima upravnim na ovu osu (ravni paralela). Meridijanske ravni seku loptinu površ po velikim krugovima tako da meridijani na lopti odgovaraju velikim krugovima. Paralele predstavljaju male krugove, osim Ekvatora koji prolazi kroz centar sfere.. Koordinatni počekat na sferi definisan je presekom Ekvatora i usvojenog početnog meridijana (koji prolazi kroz Griničku observatoriju).

Meridijani i paralele na sferi predstavljaju parametarske, tj. koordinatne linije, to je jedna od mogućih parametrizacija. Pozicija bilo koje tačke na sferi može se definisati presekom jednog meridijana i jedne paralele. Kod slučaja kada smo imali ravan gde je bilo koja tačka određena presekom samo jedne x i samo jedne y koordinatne linije, to je slučaj regularne parametrizacije površi. Kod sfere imamo slučaj da postoje i singularne tačke, a to su polovi u kojima se sustiče svaki meridijan, a poluprečnik paralele u polovima je 0. Polovi nisu određeni presekom samo jedne paralele i samo jednog meridija, zato su to singularne tačke, pa i parametrizacija sfere meridijanima i paralelama nije u potpunosti regularna parametrizacija površi.

Geografske krivolinijske koordinate \(\varphi\) i \(\lambda\) na sferi

Koordinatne linije paralela zadaju se geografskom širinom \(\varphi\) (ugao koji radijus Zemlje u odnosnoj tački zaklapa sa ekvatorskom ravni) i geografskom dužinom \(\lambda\) (ugao koji ravan meridijana odnosne tačke zaklapa sa ravni početnog meridijana). Tako da je svaka koordinata definisana parom krivolinijskih koordinata geografskom širinom i dužinom, \(\varphi\) i \(\lambda\).

Ako zadamo koordinate tačke GRF sa geografskom širinom (\(\varphi=44.8057705\)) i dužinom (\(\lambda=20.4759749\)) u stepenima, i prestavimo na virtuelnom globusu, dobija se prikaz, Slika 2.7. Dakle tu tačku definiše presek koordinatne linije paralele sa g. širinom 44.8057705 i meridijana sa g. dužinom 20.4759749 stepeni. U narednom primeru su korišćeni R paketi, webglobe (Barnes 2020) i plotKML (Hengl et al. 2015).

Code 
# install.packages("webglobe")
library(webglobe)


wg <- webglobe(immediate=FALSE)
wg <- wg + wgpoints(44.8057705,20.4759749,label="Beograd GRF",alt=0,colour="blue")
wg

# Drugi prikaz na Google Earth 
library(sf)
library(plotKML)
grf = st_point( c(20.4759749, 44.8057705) )
att = data.frame(Pozicija = c("lon:20.4759749, lat:44.8057705"))
grf = st_sf(att, geometry =  st_sfc(grf, crs=4326 ) )

#tacke na meridijanu g. dužina je konstanstna
m = as.matrix( data.frame(x=rep(20.4759749,100), y=seq(-90,90,length.out=100) ))
# tacke na paraleli g.širina je konstantana
p = as.matrix(data.frame(x=seq(-180,180,length.out=100), y= rep(44.8057705,100)))
# meridijan i paralela tačke GRF              
mip =  st_sf(data.frame(ime=c("meridijan", "paralela"),
                        st_sfc( st_linestring(m), 
                                st_linestring(p),crs=4326) ))

# Grinič
g = as.matrix( data.frame(x=rep(0,100), y=seq(-90,90,length.out=100) ))
# Ekvator
e = as.matrix(data.frame(x=seq(-180,180,length.out=100), y= rep(0,100)))
# Grinič i Ekvator            
gie = st_sf(data.frame(ime=c("meridijan", "paralela"),
                        st_sfc( st_linestring(g),           
                               st_linestring(e),crs=4326) ))

plotKML(grf)
plotKML(mip)
plotKML(gie, colour="red")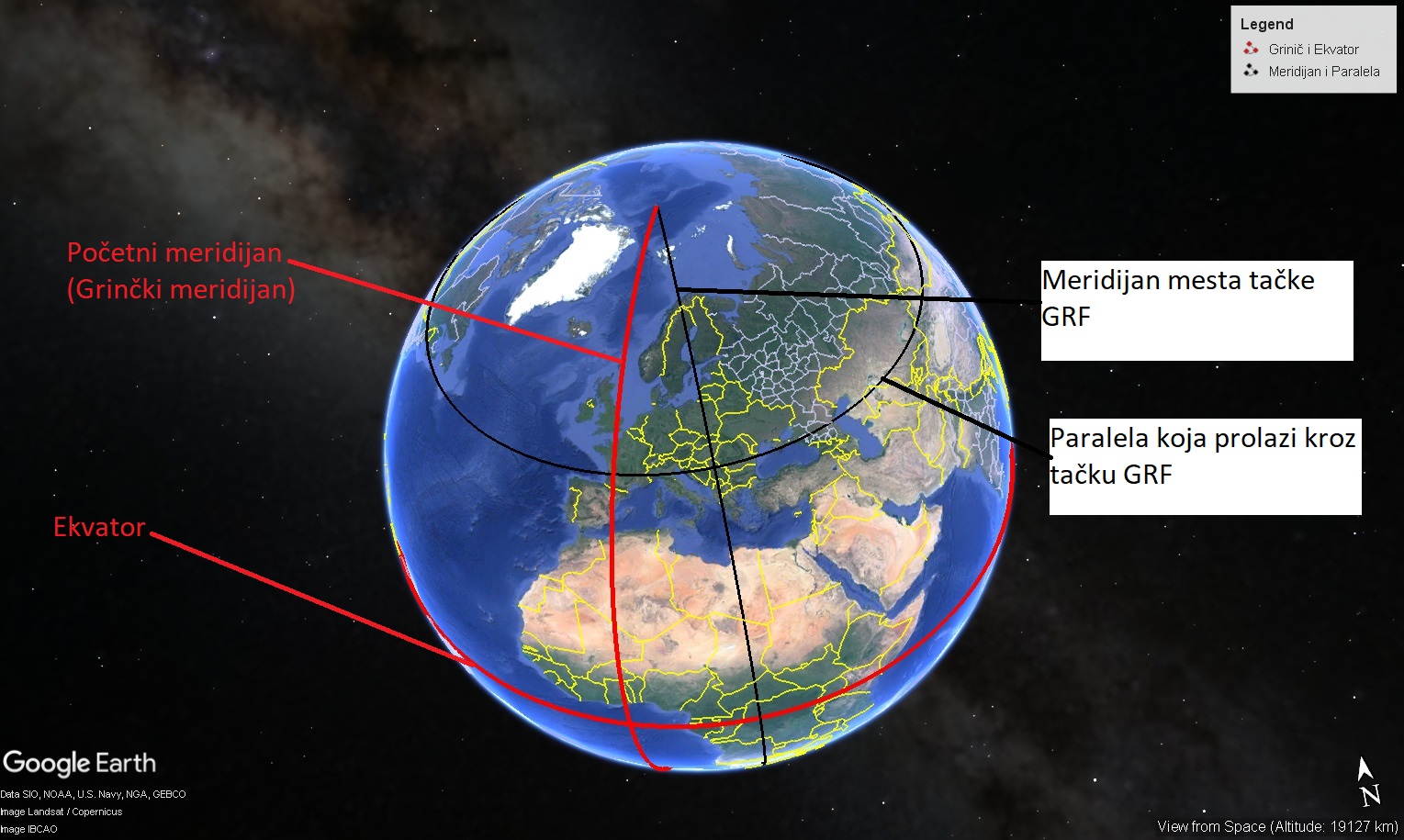

Slika 2.7: Pravougle koordinate na sferi.

Pravougle koordinate na sferi

Slika 2.8 prikazuje pravougle koordinate na sferi.

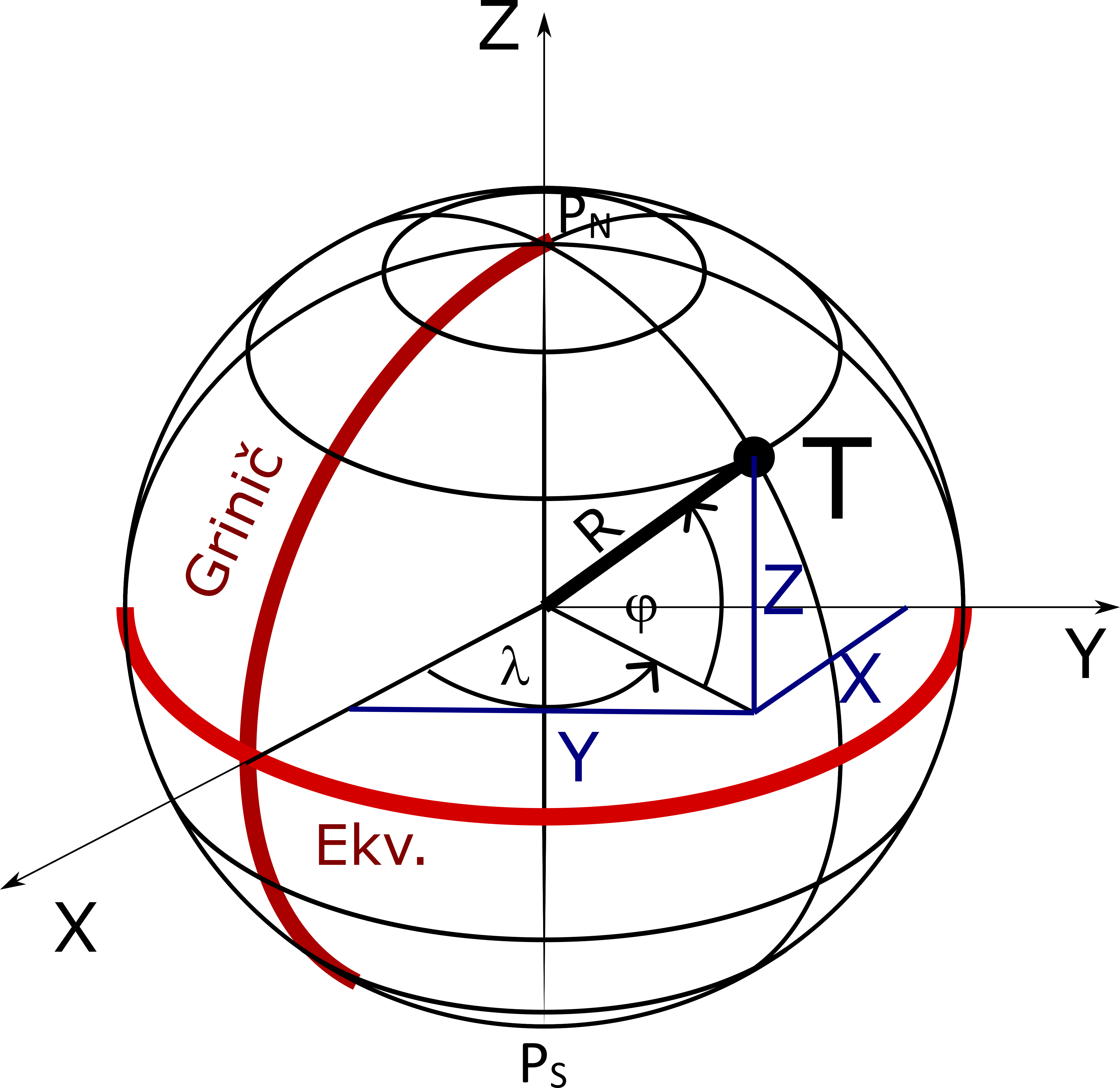
Slika 2.8: Geografske koordinate na sferi, primer GRF.

Formule za pravougle koordinate na sferi, ako su nam poznate krivolinijske zadate geografskom širinom i dužinom, \(\varphi\) i \(\lambda\), i poluprečnik sfere R.

\[ \begin{aligned} & X=R \cos \varphi \cos \lambda, \\ & Y=R \cos \varphi \sin \lambda, \\ & Z=R \sin \varphi . \end{aligned} \]

Obrnuto, ako znamo pravougle možemo doći do krivolinijskih koristeći formulu:

\[ \begin{aligned} & \varphi=\operatorname{asin}(\mathrm{Z} / \mathrm{R}) \\ & \lambda=\operatorname{atan2}(\mathrm{Y}, \mathrm{X}) \end{aligned} \]

Polarne sferne koordinate

Sfera ili elipsoid se mogu zadati koristeći i polarne koordinate. U ovom poglavlju biće definisane samo sferne polarne koordinate, a na sličan način mogle bi biti definisane i elipsoidne polarne koordinate.

Slika 2.9: Polarne sferne koordinate.

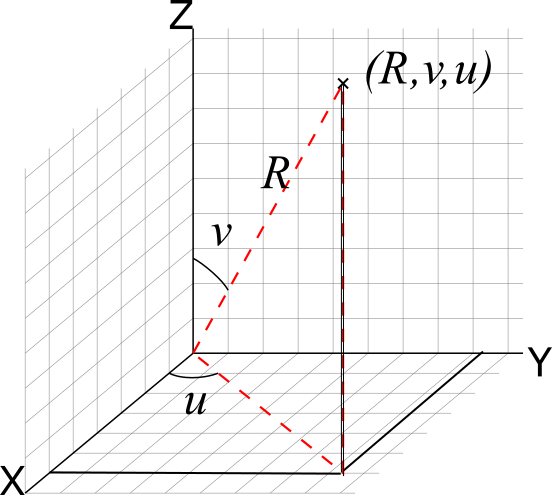
Odnos polarnih i pravouglih koordinata na sferi je sledeći: \[ \begin{aligned} & X=R \cos u \sin v, \\ & Y=R \sin u \sin v, \\ & Z=R \cos v \end{aligned} \] Gde je R poluprečnik sfere, v je deklinacija i u je pravac projekcije radijusa u ravni u odnosu na X osu.

Poluprečnik krivine meridijana i paralele

Poluprečnik krivine meridijana jeste poluprečnik meridijanskog luka. To je veliki krug na sferi, poluprečnika R.

Poluprečnik krivine paralele za tačku T je poluprečnik paralele (malog kruga) koji prolazi kroz tačku T, Slika 2.8.

\[ r=R \cos \varphi \]

Dužina luka meridijana i paralele

Ako uočimo luk TE, Slika 2.6, jasno je da iz definicije ugla u radijanima važi:

\[ \varphi=\mathrm{TE} / \mathrm{R} \] Odvade sledi: \[ \mathrm{Lm}=\mathrm{TE}=\mathrm{R} \varphi, \quad \varphi \text { je u radijanima } \] Deo luka između \(\varphi_1\) i \(\varphi_2\)

\[ \mathrm{Lm}=\mathrm{R}\left(\varphi_1-\varphi_2\right) \] Slično luk paralele imamo:

\[ \operatorname{Lp}=r\left(\lambda_1-\lambda_2\right)=\operatorname{Rcos} \varphi\left(\lambda_1-\lambda_2\right) \] Uglovi su u radijanima.

Površina sfernog trapeza

Površina sfernog trapeza se odnosi na deo išrafiran na slici, Slika 2.10.

Slika 2.10: Sferni trapez.

Formula za računanje površine sfernog trapeza je: \[ P=2 R^2\left(\lambda_2-\lambda_1\right) \cos \frac{\varphi_2-\varphi_1}{2} \cos \frac{\varphi_1+\varphi_2}{2} \] Uglovi su dati u radijanima.

Primer računanja elipsoidnog trapeza, koristeći R paket geosphere (Hijmans 2022).

# Instalacija paketa geosphere
# install.packages('geosphere')
library(geosphere)
# Warning: package 'geosphere' was built under R version 4.2.3
options(digits=12) # broj cifara za prikaz brojeva u konzoli

# poluprecnik sfere u m
R = 6377000
# Zadavanje tacaka fi , lam u stepenima
T1_deg = c(40, 20) 
T2_deg = c(48, 24)

# Površina eliposidnog trapeza koristeci funkciju iz geosphere paketa
# ulazni parametar f-je mora da bude matrica(ili dataframe) sa 2 kolone:
# prva je lon, druga lat
# Zadaje se svaka tacka poligona u odabranom smeru 
# (kazaljke na satu ili obrnutom), i na kraju opet pocetna tacka

p <- rbind(c(T1_deg[2], T1_deg[1]), 
           c(T1_deg[2], T2_deg[1]), 
           c(T2_deg[2], T2_deg[1]), 
           c(T2_deg[2], T1_deg[1]), 
           c(T1_deg[2], T1_deg[1]))
# površina u km2
# pošto koristimo sferu parametar sploštenosti je 0
# funkcija može da računa i na elipsoidu
round( areaPolygon(p, a = R , f= 0 ) / 1000000 , 2)
# [1] 284865.96

Geodetska linija i loksodroma na lopti

Po definiciji ‒ matematički, geodetska linija je kriva na datoj površi u čijoj se svakoj tački glavna normala krive poklapa sa odgovarajućom normalnom na površ.

Glavna karakteristika geodetske linije je da predstavlja najkraću liniju koja povezuje dve zadate tačke na bilo kojoj analitički određenoj površi. Ovu osobinu imaju prava u ravni i luk velikog kruga lopte, između dveju tačaka, pa se za njih može reći da su to svojevrsne geodetske linije na ravni, odnosno na lopti. Pri tome, treba imati u vidu da se u matematičkoj kartografiji za najkraću udaljenost između dve tačke na lopti, tj. za luk velikog kruga, koristi termin ortodroma.

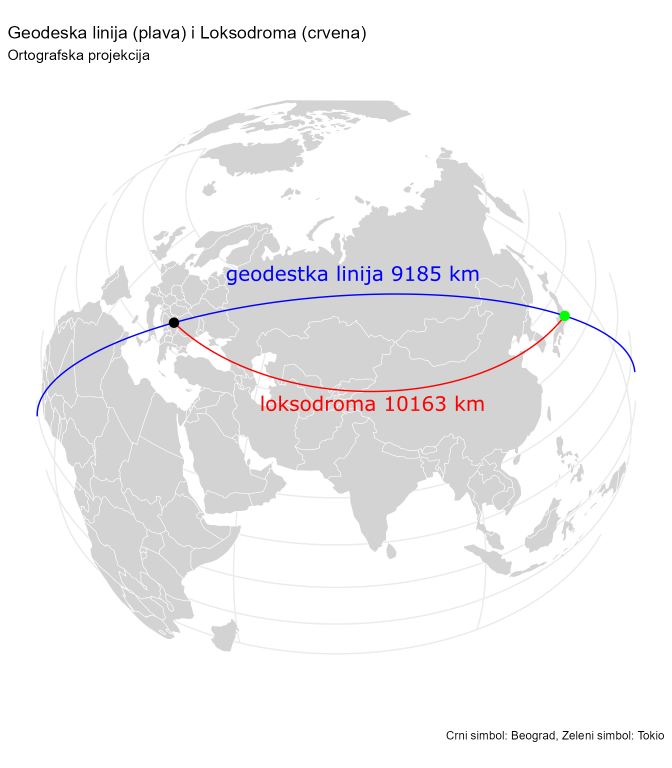
Kriva na površi Zemljinog elipsoida, koja sve meridijane seče pod istim uglom (azimutom) naziva se loksodroma. Ovo svojstvo je čini podesnom za navigaciju, jer omogućava da se po njoj putuje (plovi ili leti) sa konstantnim kursom. Slika 2.11 daje shematski prikaz loksodrome između tačaka T1 i T2.

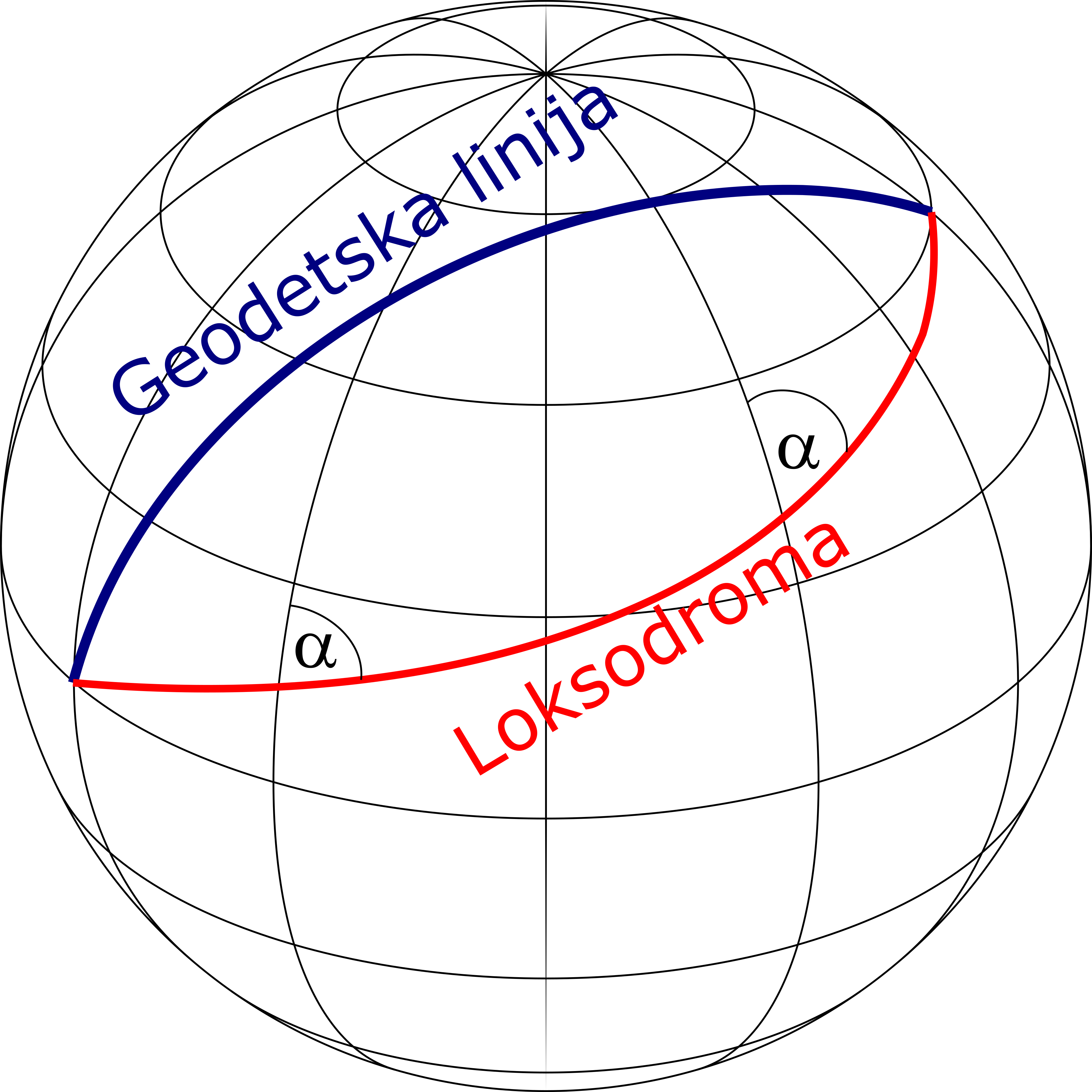
Slika 2.11: Odnos geodetske linije, ortodrome i loksodrome na sferi.

U sledećem primeru je izračunata dužina između Beograda i Tokija po geodetskoj liniji i loksodromi, koristeći R paket geosphere, (Hijmans 2022), poluprečnik kojim se aproksimira Zemlja je uzet da je 6.377 km.

library(geosphere)
# poluprecnik sfere u m
R = 6377000
options(digits=12) # broj cifara za prikaz brojeva u konzoli
# Zadavanje tacaka fi , lam
T1_deg = c(44.800153, 20.455727) 
T2_deg = c(35.679207, 139.767118)

# funkcija računa geotesku liniju na elipsoidu, 
# ako kažemo da je spljoštenost 0
# onda funkcija važi i za sferu
azimut = bearingRhumb( c(T1_deg[2], T1_deg[1]), c(T2_deg[2], T2_deg[1]) )
# Loksodroma = R*(fi2-f1)*sec(alfa)
Loksodroma = R * (T1_deg[1]*pi/180- T2_deg[1]*pi/180 ) / abs(cos(azimut*pi/180))


Ortodroma = distGeo(c(T1_deg[2], T1_deg[1]), c(T2_deg[2], T2_deg[1]), a=R, f=0)

options(digits=12)
round(Ortodroma,2)
# [1] 9206566.75
round(Loksodroma,2)
# [1] 10161491.81

#razilka u dužini u m
round(Loksodroma-Ortodroma,2)
# [1] 954925.07

#razilka u dužini u km
round((Loksodroma-Ortodroma)/1000,2)
# [1] 954.93

2.4 Koordinate na elipsoidu

U diferencijalnoj geometriji obrtnom površi smatra se površ nastala obrtanjem neke krive oko zamišljene ose. Linije preseka ove površi sa ravnima koje prolaze kroz obrtnu osu nazivaju se meridijani, a linije preseka sa ravnima upravnim na obrtnu osu nazivaju se paralele. U geodeziji se pod obrtnim Zemljinim elipsoidom podrazumeva geometrijsko telo koje nastaje obrtanjem elipse oko njene male ose, Slika 2.12.

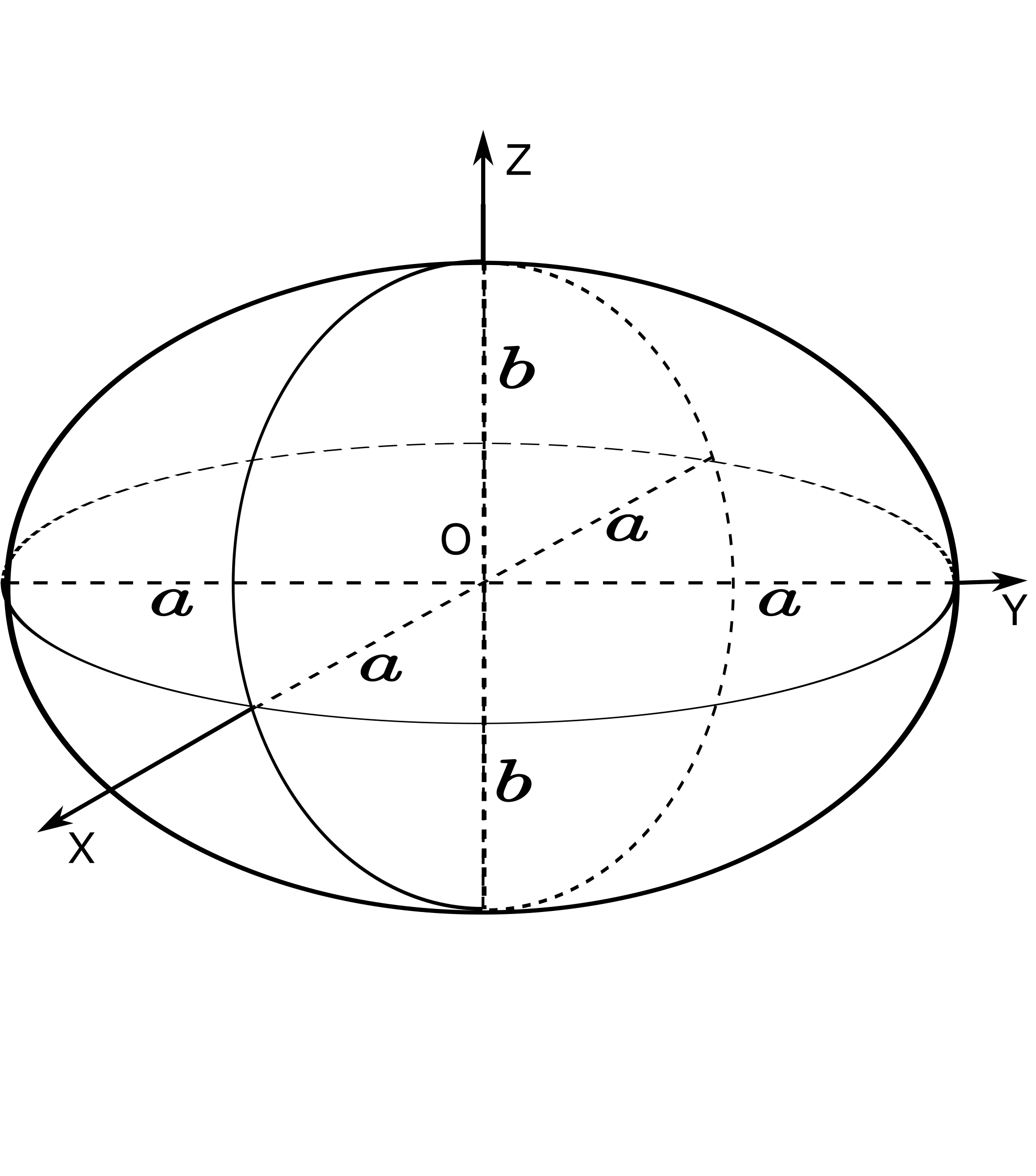
Slika 2.12: Obrtni elipsoid za aproksimaciju Zemlje.

Ravni koje sadrže obrtnu osu elipsoida nazivaju se meridijanske ravni i te ravni koje sadrže obrtnu osu seku površ elipsoida seku po meridijanskim elipsama. Ravan koja je upravna na obrtnu osu i prolazi kroz centar elipsoida naziva se ekvatorijalna ravan. Ona preseca elipsoid po najvećem paralelnom krugu (poluprečnika a, koliko je i velika poluosa elipsoida), koji se naziva Ekvator, sve ostale paralele su manji krugovi. Meridijani i paralele predstavljaju jednu od parametricija elipsoida, slično kao kod sfere. Polovi su singularne tačke.

Elipsoid kojim se aproksimira oblik Zemlje je dvoosni elipsoid i zadaje se sa dva linearno nezavisna parametra. Na primer:

  • velikom i malom poluosom elipsoida (a, b),

  • velikom poluosom i spljoštenošću (a, f), ili

  • velikom osom i prvim numeričkim ekscentricitetom (a, e), Tabela 2.1.

Tabela 2.1: Parametri elipsoida.
Parametar Opis
a Velika poluosa
f = (a-b)/a Spljoštenost
b = a- fa Mala poluosa
e2 = 2f -f 2 Prvi numerički ekscentricitet
e’ 2 = (2f - f 2)(1 - f )–2 Drugi numerički ekscentricitet

U geodeziji se koristi veliki broj elipsoida za aproksimaciju planete Zemlje. Ovde su dati neki zadati sa 2 linearno nezavisna parametra, velikom poluosom i inverznom spljoštenošću (1/f):

 MERIT a=6378137.0 rf=298.257 MERIT 1983                           
 SGS85 a=6378136.0 rf=298.257 Soviet Geodetic System 85            
 GRS80 a=6378137.0 rf=298.257222101 GRS 1980(IUGG, 1980)           
 IAU76 a=6378140.0 rf=298.257 IAU 1976                             
 airy a=6377563.396 b=6356256.910 Airy 1830                        
 APL4.9 a=6378137.0. rf=298.25 Appl. Physics. 1965                 
 NWL9D a=6378145.0. rf=298.25 Naval Weapons Lab., 1965             
 mod_airy a=6377340.189 b=6356034.446 Modified Airy               
 andrae a=6377104.43 rf=300.0 Andrae 1876 (Den., Iclnd.)           
 aust_SA a=6378160.0 rf=298.25 Australian Natl & S. Amer. 1969    
 GRS67 a=6378160.0 rf=298.2471674270 GRS 67(IUGG 1967)             
 bessel a=6377397.155 rf=299.1528128 Bessel 1841                   
 bess_nam a=6377483.865 rf=299.1528128 Bessel 1841 (Namibia)      
 clrk66 a=6378206.4 b=6356583.8 Clarke 1866                        
 clrk80 a=6378249.145 rf=293.4663 Clarke 1880 mod.                 
 clrk80ign a=6378249.2 rf=293.4660212936269 Clarke 1880 (IGN).     
 CPM a=6375738.7 rf=334.29 Comm. des Poids et Mesures 1799         
 delmbr a=6376428. rf=311.5 Delambre 1810 (Belgium)                
 engelis a=6378136.05 rf=298.2566 Engelis 1985                     
 evrst30 a=6377276.345 rf=300.8017 Everest 1830                    
 evrst48 a=6377304.063 rf=300.8017 Everest 1948                    
 evrst56 a=6377301.243 rf=300.8017 Everest 1956                    
 evrst69 a=6377295.664 rf=300.8017 Everest 1969                    
 evrstSS a=6377298.556 rf=300.8017 Everest (Sabah & Sarawak)       
 fschr60 a=6378166. rf=298.3 Fischer (Mercury Datum) 1960          
 fschr60m a=6378155. rf=298.3 Modified Fischer 1960                
 fschr68 a=6378150. rf=298.3 Fischer 1968                          
 helmert a=6378200. rf=298.3 Helmert 1906                          
 hough a=6378270.0 rf=297. Hough                                   
 intl a=6378388.0 rf=297. International 1909 (Hayford)             
 krass a=6378245.0 rf=298.3 Krassovsky, 1942                       
 kaula a=6378163. rf=298.24 Kaula 1961                             
 lerch a=6378139. rf=298.257 Lerch 1979                            
 mprts a=6397300. rf=191. Maupertius 1738                          
 new_intl a=6378157.5 b=6356772.2 New International 1967          
 plessis a=6376523. b=6355863. Plessis 1817 (France)               
 SEasia a=6378155.0 b=6356773.3205 Southeast Asia                  
 walbeck a=6376896.0 b=6355834.8467 Walbeck                        
 WGS60 a=6378165.0 rf=298.3 WGS 60                                 
 WGS66 a=6378145.0 rf=298.25 WGS 66                                
 WGS72 a=6378135.0 rf=298.26 WGS 72                                
 WGS84 a=6378137.0 rf=298.257223563 WGS 84                         
 sphere a=6370997.0 b=6370997.0 Normal Sphere (r=6370997)

Geodetske koordinate na elipsoidu

Geodetska širina \(\varphi\) je ugao u ravni meridijana, između ravni Ekvatora i normale na elipsoidu koja prolazi kroz tačku P. Geodetska dužina \(\lambda\) je ugao između ravni početnog meridijana (najčešće Grinički meridijan) i meridijanske ravni koja prolazi kroz tačku P. Geodetska (elipsoidna) visina h je geometrijska udaljenost od površi elipsoida (gde je h=0 m) do tačke P na fizičkoj površi Zemlje merena duž normale na elipsoidu, P’P (Slika 2.13).

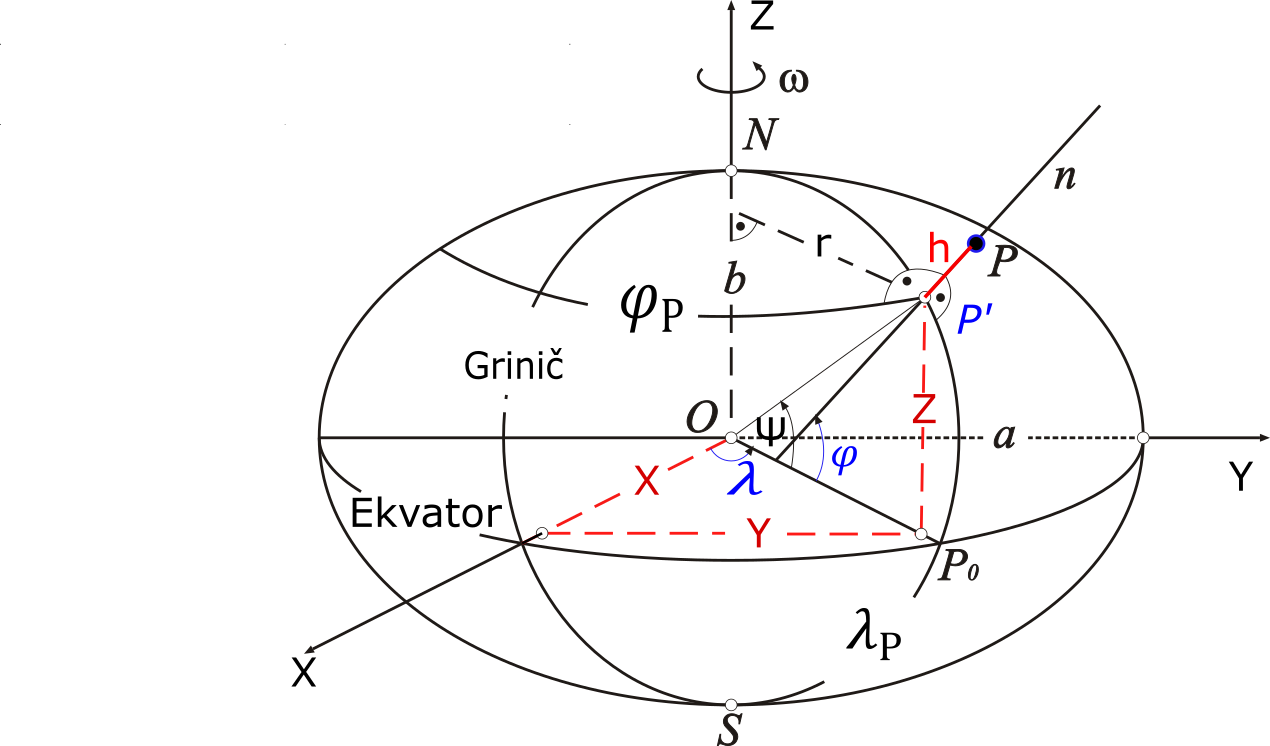
Slika 2.13: Obrtni elipsoid za aproksimaciju Zemlje sa prikazom koordinata. Modifikovan izvor: https://commons.wikimedia.org/wiki/File:Earth_ellipsoid.svg

Na slici može se oučiti ugao \(\psi\) (Slika 2.13) koji predstavlja geocentričnu širinu.

Normalni preseci i poluprečnici krivina

Ako površ elipsoida presečemo ravnima koje prolaze kroz normalnu na elipsoid u nekoj tački, nastaju krive linije koje nazivamo normalnim presecima. Razumljivo je da se kroz normalu svake tačke može postaviti beskonačno mnogo ravni i da će svaka od njih imati odgovarajući normalni presek. No, između bezbroj normalnih preseka postoje dva, međusobno upravna, tzv. glavni normalni preseci, koji su veoma značajni za površ elipsoida, pa i za primenu u matematičkoj kartografiji.

Slika 2.14: Normalni preseci.

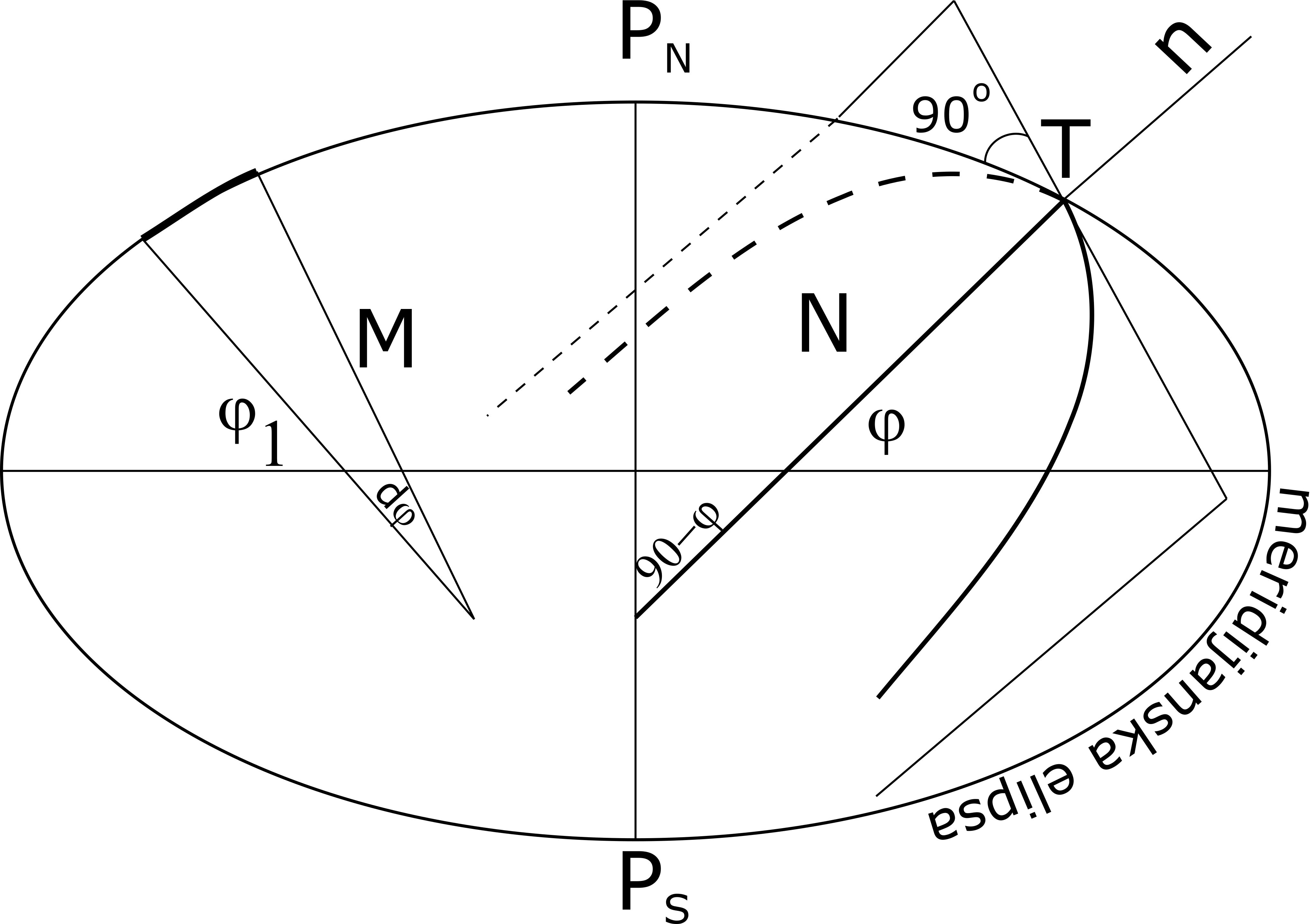
Meridijansku ravan definiše normala u tački T i pol PN, Slika 2.14. Ravan koja sadrži normalu u tački T, a upravna je na meridijansku ravan jeste ravan prvog vertikala. Presek ravni prvog vertikala sa elipsoidom definiše elipsu prvog vertikala. Meridijanski presek i prvi vertikal su glavni preseci.

Poluprečnik krivine meridijana

Meridijansku ravan definiše normala u tački T i pol PN, Slika 2.15. Da bismo izveli formulu za poluprečnik krivine u tački T, prethodno treba naći vezu između ravanskih pravouglih koordinata \(x\) i \(y\) u ravni meridijana i geodetske širine \(\varphi\).

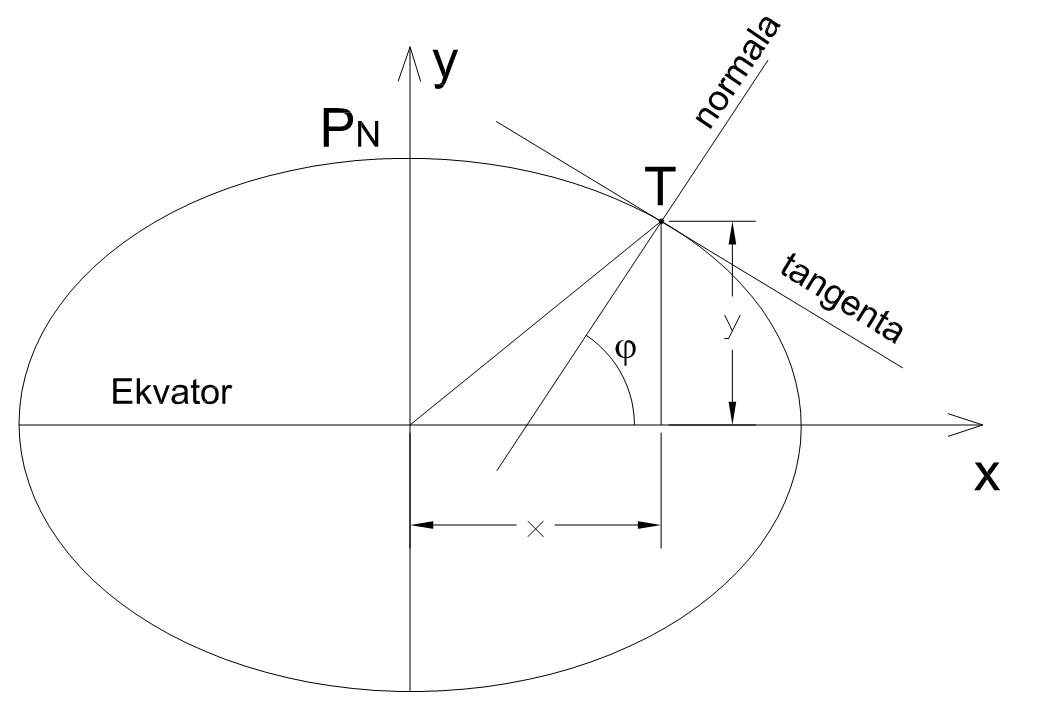
Slika 2.15: Meridijanska ravan i pravougle koordinate u meridijanskoj ravni.

Jednačina meridijanske elipse je:

\[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \]

Diferenciranjem se dobija:

\[ \frac{2 x d x}{a^2}+\frac{2 y d y}{b^2}=0 \]

Odakle sledi da je prvi izvod y po x:

\[ \frac{d y}{d x}=-\frac{b^2}{a^2} \frac{x}{y} \]

Iz definicije prvog izvoda znamo da je to nagib tangente u posmatranoj tački, pa možemo da znamo i koliki je nagib normale u posmatranoj tački, Slika 2.15. Jasno je sa slike da je ugao koji tangenta zaklapa sa x osom u smeru suprotnom kazaljci na satu, \(90+\varphi\), a još je lakše uočiti da je ugao u smeru kazaljke na satu \(90-\varphi\). Dakle, možemo pisati da važi:

\[ \frac{d y}{d x}=-\frac{b^2}{a^2} \frac{x}{y}=\tan (\varphi+90) \]

Odakle sledi da je:

\[ \begin{aligned} & \tan \varphi=\frac{a^2}{b^2} \frac{y}{x} \\ & y=\frac{b^2}{a^2} x \tan \varphi \end{aligned} \]

Znajući da je prvi numerički ekscentricitet elipse zadat formulom:

\[ e^2=1-\frac{b^2}{a^2} \]

Dobijamo:

\[ y=x\left(1-e^2\right) \tan \varphi \] Ako se vratimo na jednačinu elipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), lako možemo rešiti jednačinu elipse po x (zamenimo y), a potom po y i dobiti vezu između ravanskih pravouglih koordinata x i y u ravni meridijana i geodetske širine \(\varphi\).

\[ \begin{aligned} & x=\frac{a \cos \varphi}{\sqrt{1-e^2 \sin ^2 \varphi}} \\ & y=\frac{a\left(1-e^2\right) \sin \varphi}{\sqrt{1-e^2 \sin ^2 \varphi}} \end{aligned} \] Neka su T i T’ tačke koje su na infinitezimalnom rastojanju, Slika 2.16, tako da element ds možemo posmatrati kao linearan. Poluprečnik krivine meridijana u tački T se onda može sračunati kao:

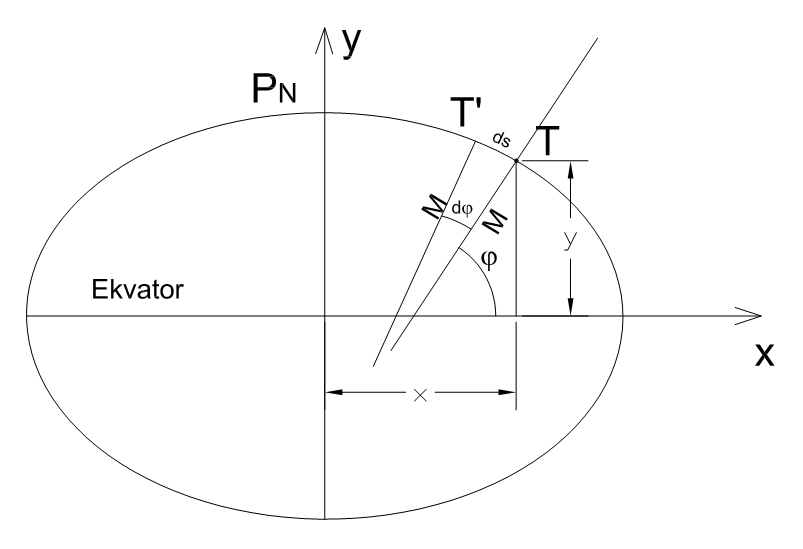
Slika 2.16: Poluprečnik krivine meridijana.

\[ M=\frac{d s}{d \varphi}=\frac{\sqrt{d x^2+d y^2}}{d \varphi} \Rightarrow \quad M=\sqrt{\left(\frac{d x}{d \varphi}\right)^2+\left(\frac{d y}{d \varphi}\right)^2} \] Diferenciranjem pravouglih koordinata x i y dobija se:

\[ \begin{aligned} & \frac{d x}{d \varphi}=\frac{a\left(1-e^2\right) \sin \varphi}{\sqrt{\left(1-e^2 \sin ^2 \varphi\right)^3}} \\ & \frac{d y}{d \varphi}=\frac{a\left(1-e^2\right) \cos \varphi}{\sqrt{\left(1-e^2 \sin ^2 \varphi\right)^3}} \end{aligned} \]

Konačno dobijamo formulu za računanje poluprečnika krivine meridijana:

\[ M=M(\varphi)=\frac{(a b)^2}{\left((a \cdot \cos \varphi)^2+(b \cdot \sin \varphi)^2\right)^{\frac{3}{2}}}=\frac{a\left(1-e^2\right)}{\left(1-e^2 \sin ^2 \varphi\right)^{\frac{3}{2}}} \]

Ceo postupak je mogao biti mnogo kraći, čim smo došli do formula za x i y u zavisnosti od \(\varphi\) mogli smo direktno primeniti formulu za računanje poluprečnika krivine i dobiti rezultat, računajući prvi i drugi izvod.

\[ M=\frac{\left(y^{\prime \prime}\right)^2}{\left(1+\left(y^{\prime}\right)^2\right)^{\frac{3}{2}}}=\frac{\frac{d^2 y}{d x^2}}{\left(1+\left(\frac{d y}{d x}\right)^2\right)^{\frac{3}{2}}} \]

Poluprečnik krivine paralele i poluprečnik krivine po prvom vertikalu

Kao što je već rečeno, ravan koja sadrži normalu u tački T, a upravna je na meridijansku ravan, jeste ravan prvog vertikala. Presek ravni prvog vertikala sa elipsoidom definiše elipsu prvog vertikala u tački T čiji poluprečnik krivine u tački T tražimo, Slika 2.17.

Slika 2.17: Poluprečnik krivine prvog vertikala N i poluprečnik krivine paralele r.

Sa slike se jasno uočava trougao cTn , sa r je označen poluprečnik krivine paralele, odnosno poluprečnik paralele (paralela je mali krug na elipsoidu, paralelna ekvatorijalnom krugu). Takođe, lako je uočiti da je r=x, apscisi u ravni meridijana. Dakle, poluprečnik paralele je:

\[ r=x=\frac{a \cos \varphi}{\sqrt{1-e^2 \sin ^2 \varphi}} \] Iz trougla cTn je jednostavno naći formulu za računanje poluprečnika krivine po prvom vertikalu:

\[ N=N(\varphi)=\frac{r}{\cos \varphi}=\frac{x}{\cos \varphi}=\frac{a}{\sqrt{1-e^2 \sin ^2 \varphi}} \] Znajući formulu za N može se definisati i drugi oblik formule za poluprečnik krivine meridijana:

\[M(\varphi)=\frac{1-e^2}{a^2} N(\varphi)^3\]

Do formule za poluprečnik krivine paralele moglo se doći i koristeći teoremu Menjea, kojom se definiše odnos kosog preseka (u našem slučaju paralele) i normalnog preseka (u ovom slučaju prvog vertikala).
Teorema Menjea: Poluprečnik krivine kosog preseka jednak je proizvodu poluprečnika krivine normalnog preseka i kosinusa ugla između normalnog i kosog preseka.

Poluprečnik krivine u proizvoljnom pravcu

Ojlerova formula za poluprečnik krivine normalnog preseka u proizvoljnom (azimutu) pravcu je:

\[ \frac{1}{r}=\frac{\cos ^2 \alpha}{M}+\frac{\sin ^2 \alpha}{N} \] odakle sledi da je poluprečnik krivine normalnog preseka u pravcu azimuta \(\alpha\):

\[ r=\frac{M N}{N \cos ^2 \alpha+M \sin ^2 \alpha} \]

Srednji poluprečnik krivine

Srednji poluprečnik krivine je aritmetička sredina iz poluprečnika krivina svih normalnih preseka u tački T.

\[ r_0=\frac{1}{2 \pi} \int_0^{2 \pi} \frac{M N}{N \cos ^2 \alpha+M \sin ^2 \alpha}=\sqrt{M N}=\frac{a \sqrt{1-e^2}}{1-e^2 \sin ^2 \varphi} \]

Dužina meridijanskog luka

Uzmimo na meridijanu dve proizvoljno bliske tačke T1 i T2, čije su širine \(\varphi\) i \(\varphi +d\varphi\). Normale u ovim tačkama, odnosno radijusi krivina meridijanskog luka, zaklapaće ugao \(d\varphi\), Slika 2.18. Pošto su tačke na ifinitezimalnoj (nemreljivoj) maloj udaljenosti, možemo smatrati da je poluprečnik krivine meridijana i u jednoj i u drugoj tački M.

Slika 2.18: Dužina luka meridijana.

Onda imamo da dužinu \(dL_m\) možemo dobiti iz definicije ugla u radijanima:

\[ dL_m= M d \varphi \] Jasno je da možemo dobiti i ukupnu dužinu meridijanskog luka, ako integralimo prethodni izraz:

\[ L_m=\int_{\varphi_1}^{\varphi_2} M d \varphi \]

Rešenje ovog integrala daje nam opštu formulu za dužinu luka meridijana (Jovanović 1984):

\[ \begin{aligned} L_m & =a\left(1-e^2\right)\left[A\left(\varphi_2-\varphi_1\right)-\frac{B}{2}\left(\sin 2 \varphi_2-\sin 2 \varphi_1\right)+\right. \\ & \left.+\frac{C}{4}\left(\sin 4 \varphi_2-\sin 4 \varphi_1\right)-\frac{D}{6}\left(\sin 6 \varphi_2-\sin 6 \varphi_1\right)+\ldots\right] \end{aligned} \]

gde su:

\[ \begin{aligned} & A=1+\frac{3}{4} e^2+\frac{45}{64} e^4+\frac{175}{256} e^6+\ldots \\ & B=\frac{3}{4} e^2+\frac{15}{16} e^4+\frac{525}{512} e^6+\ldots \\ & C=\quad \frac{15}{64} e^4+\frac{105}{256} e^6+\ldots \\ & D=\quad \frac{35}{256} e^6+\ldots \\ & \end{aligned} \]

Uglovi su izraženi u radijanima, e predstavlja prvi numerički ekscentricitet.

U sledećem primeru sračunata je dužina meridijanskog luka na dva načina na Beselovom elipsoidu.

# Zadavanje tacaka fi , lam
T1_deg = c(43,21) 
T2_deg = c(45,23)

# Duzina meridijanskog luka na elipsoidu
M = function(fi,  a=6377397.155 , rf=299.1528128 ){
  f = 1/rf
  e = sqrt(2*f - f^2)
  M = a*(1-e^2)/(1-e^2*sin(fi)^2)^(3/2)
  return(M)
}
fi1 = T1_deg[1] * pi/180 # stepeni u radijane
fi2 = T2_deg[1] * pi/180 # stepeni u radijane
# Integral -  numeričko rešenje integrala
Lm = integrate(M, lower=fi1, upper=fi2, rel.tol=0.1)$value
# u m
round(Lm,2)
# [1] 222200
# u km
round(Lm/1000,2)
# [1] 222

# Drugi način po gore datoj formuli

dmer  <- function( lat1deg,  lat2deg, a=6377397.155 , rf=299.1528128) {
  f = 1/rf
  e = sqrt(2*f - f^2)
  fi1 = lat1deg*pi/180
  fi2 = lat2deg*pi/180
  A = 1 + 3 / 4 * e^2 + 45 / 64 * e^4 + 175 / 256 * e^6
  B = 3 / 4 * e^2 + 15 / 16 * e^4 + 525 / 512 * e^6
  C= 15 / 64 * e^4 + 105 / 256 * e^6
  D= 35/256 *e^6

  Lm = a*(1-e^2)*(A*(fi2-fi1)-B/2*(sin(2*fi2) - sin(2*fi1)) + 
                    C/4*(sin(4*fi2) - sin(4*fi1)) -
                    D/6 *(sin(6*fi2) - sin(6*fi1) ) )
  return(abs(Lm))
}

Lm2 = dmer(T1_deg[1], T2_deg[1])  # dmer(43,45)

# u m
round(Lm2,2)
# [1] 222200
# u km
round(Lm2/1000,2)
# [1] 222

Dužina luka paralele

Paralele su na obrtnom elipsoidu krugovi, Slika 2.17, računanje dužina lukova paralela svodi se na određivanje kružnih lukova sa centralnim uglom jednakim razlici geodetskih dužina krajnjih tačaka luka:

\[ L_p=N_{\varphi}\left(\lambda_2-\lambda_1\right) \cos \varphi \]

Površina elipsoidnog trapeza

Uočimo elipsoidni trapez na slici (Slika 2.19). Primenićemo sličan postupak kao kod računanja dužine meridijanskog luka.

Slika 2.19: Površina elipsoidnog trapeza.

Jasno je da površinu elipsoidnog trapeza možemo definisati kao:

\[ P=\int_{\varphi_1}^{\varphi_2} \int_{\lambda_1}^{\lambda_2} M N \cos \varphi d \varphi d \lambda \]

Rešenje integrala je (Jovanović 1984):

\[ \begin{aligned} P= & a^2\left(1-e^2\right) \left(\lambda_2-\lambda_1\right)\left[A\left(\sin \varphi_2-\sin \varphi_1\right)-B\left(\sin 3 \varphi_2-\sin 3 \varphi_1\right)+\right. \\ & \left.+C\left(\sin 5 \varphi_2-\sin 5 \varphi_i\right)-D\left(\sin 7 \varphi_2-\sin 7 \varphi_1\right)+\ldots\right] \end{aligned} \]

gde su: \[ \begin{aligned} & A=1+\frac{e^2}{2}+\frac{3}{8} e^4+\frac{5}{16} e^6+\ldots \\ & B=\frac{e^2}{6}+\frac{3}{10} e^4+\frac{3}{16} e^6+\ldots \\ & C=\quad \frac{3}{80} e^4+\frac{4}{16} e^6+\ldots \\ & D=\quad \frac{1}{112} e^6+\ldots \\ & \end{aligned} \]

e je prvi numerički ekscentricitet elipsoida koji se koristi, uglovi su u radijanima.

Primer računanja elipsoidnog trapeza, koristeći R paket geosphere (Hijmans 2022), na elipsoidu WGS84.

# Instalacija paketa geosphere
# install.packages('geosphere')
library(geosphere)
options(digits=12) # broj cifara za prikaz brojeva u konzoli

#  WGS84 a=6378137.0 rf=298.257223563 WGS 84 
a=6378137
f=1/298.257223563
# Zadavanje tacaka fi , lam u stepenima
T1_deg = c(40, 20) 
T2_deg = c(48, 24)

# Površina eliposidnog trapeza koristeci funkciju iz geosphere paketa
# ulazni parametar f-je mora da bude matrica(ili dataframe) sa 2 kolone:
# prva je lon, druga lat
# Zadaje se svaka tacka poligona u odabranom smeru 
# (kazaljke na satu ili obrnutom), i na kraju opet pocetna tacka

p <- rbind(c(T1_deg[2], T1_deg[1]), 
           c(T1_deg[2], T2_deg[1]), 
           c(T2_deg[2], T2_deg[1]), 
           c(T2_deg[2], T1_deg[1]), 
           c(T1_deg[2], T1_deg[1]))

# površina u km2 
round( areaPolygon(p, a = a , f= f ) / 1000000 , 2)
# [1] 284892.04

Primer računanja ortodrome i loksodrome na elipsoidu

Sledeći primer računa dužinu geodetske linije i loksodrome na elispoidu WGS84, od Beograda (\(\varphi=44.800153\) i \(\lambda=20.455727\)) do Tokija (\(\varphi=35.679207\) i \(\lambda=139.767118\)).


options(digits=12) # broj cifara za prikaz brojeva u konzoli

#  WGS84 a=6378137.0 rf=298.257223563 WGS 84 
a=6378137
f=1/298.257223563
# Zadavanje tacaka fi , lam u stepenima
T1_deg = c(44.800153, 20.455727) # BG
T2_deg = c(35.679207, 139.767118) # TK

# Ortodroma – sf paket sa s2 paketom
library(sf)
# Warning: package 'sf' was built under R version 4.2.3
# Linking to GEOS 3.9.3, GDAL 3.5.2, PROJ 8.2.1; sf_use_s2() is TRUE
bg = st_as_sfc("POINT(20.455727 44.800153)", crs = 4326) 
tk = st_as_sfc("POINT(139.767118 35.679207)", crs = 4326) 
sf_use_s2(TRUE) # koristi elipsoidna računanja
Or = st_distance(bg,tk)

# Kako f-ja distRhumb iz paketa geosphere računa dužinu loksodrome samo na sferi, 
# potrebno je definisati drugu f-ju koja računa dužinu loksodrome i na elipsoidu

# Loksodroma
lox  <- function(long1, lat1, long2, lat2, a=6378137, e=0.0818191908426215  ) {
  b <- a*sqrt(1-e^2)
  f <- (a-b)/a
  l1 = long1*pi/180
  l2 = long2*pi/180
  fi1 = lat1*pi/180
  fi2 = lat2*pi/180
  q1 = log( tan(pi/4+fi1/2) * ( (1-e*sin(fi1))/(1+e*sin(fi1)) )^(e/2) )
  q2 = log( tan(pi/4+fi2/2) * ( (1-e*sin(fi2))/(1+e*sin(fi2)) )^(e/2) )
  alfa = atan2((l2-l1),(q2-q1))
  A0 = 1 - 1/4*e^2 - 3/64*e^4 - 5/256*e^6 - 175/16384*e^8
  A2 = 3/8*(e^2 + 1/4*e^4 + 15/128*e^6 + 35/512*e^8)
  A4 = 15/256*(e^4 + 3/4*e^6 + 35/64*e^8 + 105/256*e^10)
  A6 = 35/3072*(e^6 + 5/4*e^8 + 315/256*e^10)
  m1 = a*(A0*fi1 - A2*sin(2*fi1) + A4*sin(4*fi1) - A6*sin(6*fi1))
  m2 = a*(A0*fi2 - A2*sin(2*fi2) + A4*sin(4*fi2) - A6*sin(6*fi2))
  s <- (m2 - m1)/cos(alfa)
  
  return(s)
}

Lo = lox(T1_deg[2], T1_deg[1], T2_deg[2], T2_deg[1], a=a, e=sqrt(2*f -f*2) )


options(digits=12)
round(Or,2)
# Units: [m]
#            [,1]
# [1,] 9184644.51
round(Lo,2)
# [1] 10163303.58

#razilka u dužini u m
round(Lo-as.numeric(Or),2)
# [1] 978659.06

#razilka u dužini u km
round((Lo-as.numeric(Or))/1000,2)
# [1] 978.66

Odnos geodetske linije i loksodrome sračunat u primeru je prikazan na karti u Azimutnoj ortografskoj projekciji, Slika 6.11.

Slika 2.20: Odnos geodetske linije i loksodrome.

Pravougle elipsoidne koordinate

Odnos krivolinijskih i pravouglih elipsoidnih koordinata (Slika 2.13) dat je izrazima:

\[ \begin{aligned} & X=(N+h) \cos \varphi \cos \lambda \\ & Y=(N+h) \cos \varphi \sin \lambda \\ & Z=\left(N\left(1-e^2\right)+h\right) \sin \varphi \end{aligned} \]

Takođe, ako znamo elipsoidne pravougle, možemo doći do krivolinijskih:

\[ \lambda=\operatorname{atan2}(\mathrm{Y}, \mathrm{X}) \]

Geodetska dužina i elipsoidna visina se dobijaju iterativnim postupkom (nekoliko iteracija, \(h_0=0\)).

\[ \begin{aligned} & \varphi_0=\arctan \frac{Z}{\sqrt{X^2+Y^2}} \\ & N_i=\frac{a}{\sqrt{1-e^2 \sin ^2 \varphi_i}} \\ & h_i=\frac{\sqrt{X^2+Y^2}}{\cos \varphi_i}-N_i \\ & \varphi_{i+1}=\arctan \left(\frac{Z}{\sqrt{X^2+Y^{-2}}}\left(1-\frac{e^2 N_i}{N_i+h_i}\right)^{-1}\right) \end{aligned} \]

2.5 Geodetski koordinatni referentni sistem

Da bi se znala tačna lokacija neke tačke u prostoru, pored koordinata te tačke na elipsoidu, potrebno je poznavati i druge parametre sistema, a to su oblik elipsoida i geodetski datum. Geodetski datum je set konstanti koje definišu položaj elipsoida u odnosu na Zemlju, u odnosu na centar mase i usvojene ose Zemlje.

Geodetski koordinatni referentni sistem

Geodetski koordinatni referentni sistem je geometrijski model u kome je definisan:

  • Model oblika zemlje (npr: elipsoid sa parametrima a i e);
  • Početni meridijan (najčešće Grinički meridijan, što se podrazumeva i često izostavlja iz definicije);
  • Geodetski datum.

Datum može biti definisan na dva načina, kao topocentrični datum i geocentrični datum.

Geocentrični datum se definiše sa sedam parametara i to na sledeći način:

  • Tri parametra koja definišu položaj referentnog elipsoida u odnosu na centar Zemlje ‒ \((\Delta X,\ \text{ΔY},\ \text{ΔZ})\) (ili tx, ty, tz);
  • Tri parametra koja definišu orijentaciju referentnog elipsoida ‒ \((\alpha,\ \beta,\ \gamma)\);
  • Parametar razmere ‒ \((\mu\ (\text{ili}\ \mu=1+s))\), parametar \(s\) je najčešće u ppm (eng. parts per million ‒ (jedan) deo na milion) jedinicama.

Slika 2.21 pokayuje odnos referentnog elipsoida (lokalnog, negeocentričnog, referenc elipsoida) i globalnog elipsoida. Globalni geocentrični elipsoid je takav da najbolje aproksimira celokupnu površ Zemlje (geoida).

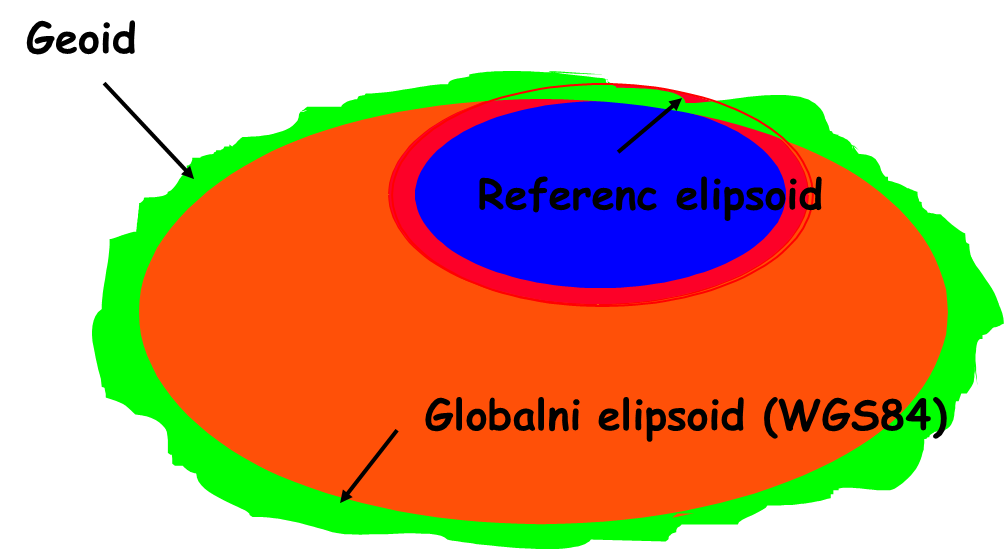
Slika 2.21: Odnos geoida, globalnog i referenc elipsoida (lokalnog elipsoida), radi ilustracije odnos je karikiran u odnosu na dimenzije.

WGS84 je konvencionalni terestrički referentni sistem uz koji se vezuje globalni elipsoid WGS84 kojim se aproksimira geoid na celoj njegovoj površini. Centar mase elipsoida se poklapa sa centrom mase Zemlje, a ose se poklapaju sa usvojenim osama Zemlje. Prema tome sedam datumskih parametara zadaju se tako da pokazuju koliko je referenc elipsoid transliran po sve tri ose u odnosu na WGS84, koliko je rotiran po sve tri ose i koliki je odnos dužina na WGS84 i referenc elipsoidu. Referenc ili lokalni elipsoid je takav da najbolje aproksimira deo površi zemlje.

Trodimenzionalnom Helmertovom transformacijom mogu se transformisati koordinate između lokalnog elipsoida i globalnog, i obrnuto. Skup pravouglih geocentričnih Dekartovih koordinata XWGS84¸ YWGS84, ZWGS84 može se transformisati u skup negeocentričnih Dekartovih koordinata XBessel¸ YBessel, ZBessel jednačinom, u ovom primeru na Beselovom elipsoidu, koji ima datum Hermanskogel (stari Državni koordinatni sistem u Srbiji), Slika 2.22.

\[ \begin{bmatrix} X^{Besel} \\ Y^{Besel} \\ Z^{Besel} \end{bmatrix} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix} + (1 + s\times10^{-6}) \cdot \begin{bmatrix} 1&-r_z&r_y \\ r_z&1&-r_x \\ -r_y & r_x & 1 \end{bmatrix} \cdot \begin{bmatrix} X^{WGS84} \\ Y^{WGS84} \\ Z^{WGS84} \end{bmatrix} \]

gde su:

  • tx, ty i tz, parametri translacije po korespondentnim koordinatnim osama,
  • s parametar razmere i
  • R matrica rotacije oko koordinatnih osa XWGS84, YWGS84 i ZWGS84.

Ukoliko su uglovi rotacije \(\alpha\), \(\beta\) i \(\gamma\) oko koordinatnih osa XWGS84, YWGS84 i ZWGS84 mali (pri transformaciji rezultata iz sistema WGS84 u lokalni koordinatni sistem, oni su reda nekoliko lučnih sekundi), onda se matrica R može predstaviti u obliku:

\[ R=\begin{bmatrix} 1&-r_z&r_y \\ r_z&1&-r_x \\ -r_y & r_x & 1 \end{bmatrix} \approx \begin{bmatrix} 1&-\gamma&\beta \\ \gamma&1&-\alpha \\ -\beta & \alpha & 1 \end{bmatrix} . \]

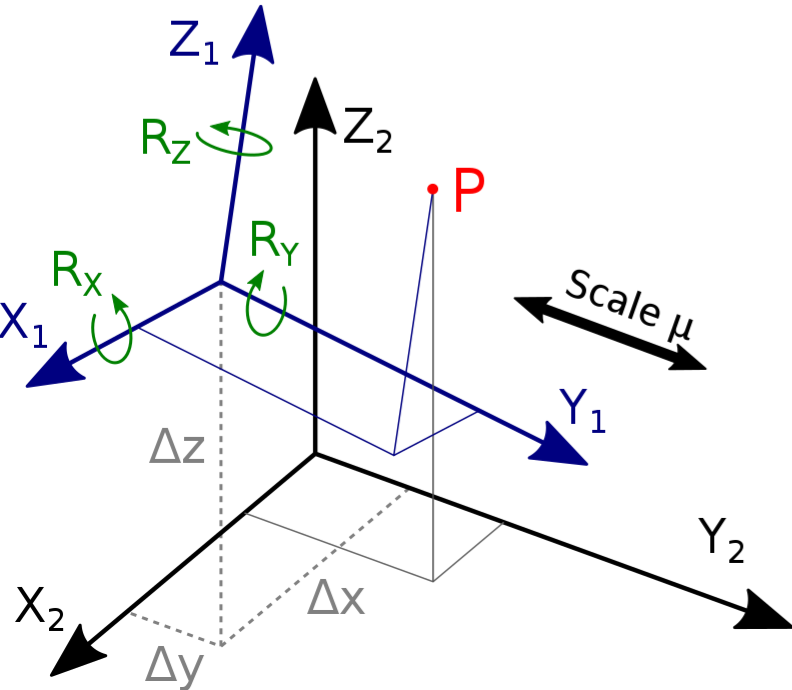
Slika 2.22: Trodimenzionalna transformacija datuma, https://w.wiki/6rCU .

Prema tome, ako je poznato sedam datumskih parametara (tx, ty, tz, \(\alpha\), \(\beta\), \(\gamma\) i s), vrednosti koordinata XBessel, YBessel, ZBessel mogu se izračunati na osnovu koordinata XWGS84¸ YWGS84, ZWGS84.

\[ \begin{matrix} X^{Bessel} & = & t_x+(1+s\times10^{-6})\cdot (X^{WGS84}-r_z\cdot Y^{WGS84}+r_y\cdot Z^{WGS84}),\\ Y^{Bessel} & = & t_y+(1+s\times10^{-6})\cdot (r_z\cdot X^{WGS84}+Y^{WGS84}-r_x\cdot Z^{WGS84}),\\ Z^{Bessel} & = & t_z+(1+s\times10^{-6})\cdot (-r_y\cdot X^{WGS84}+r_x\cdot Y^{WGS84}+Z^{WGS84}).\\ \end{matrix} \]

2.6 Koordinatni referentni sistem u projekciji

Najčešće su koordinate za prostorne podatke date kao pravougle koordinate u ravni karte, i uobičajeno je da te koordinate imaju oznaku (\(x,y\) ili \(X,Y\) ili \(E,N\)). Formule koje se koriste da se krivolinijske koordinate sa sfere ili elipsoida (geodetske koordinate) transformišu u ravan karte predstavljaju kartografske projekcije. Tada se koordinate definišu u koordinatnom referentnom sistemu u projekciji. Kod kartografskih projekcija u procesu preslikavanja dolazi do deformacija uglova (oblika), dužina i površina. Generalno, prema karakteru deformacija, projekcije se dele na konformne (zadržava se jednakost oblika, uglova), ekvivalentne (nema deformacija površina) i uslovne. Računanje pravouglih koordinata iz krivolinijskih naziva se direktni kartografski zadatak, i obratno kad se računaju krivolinijske iz pravouglih naziva se inverzni kartografski zadatak.

Detaljno o nekim projekcijama biće reči u drugom delu knjige.

Koordinatni referentni sistem u projekciji

Koordinatni referentni sistem u projekciji je geometrijski model u kome je definisana:

  • Projekcija;
  • Model oblika zemlje (npr: elipsoid sa parametrima a i e);
  • Početni meridijan (npr: Grinički meridijan);
  • Geodetski datum.

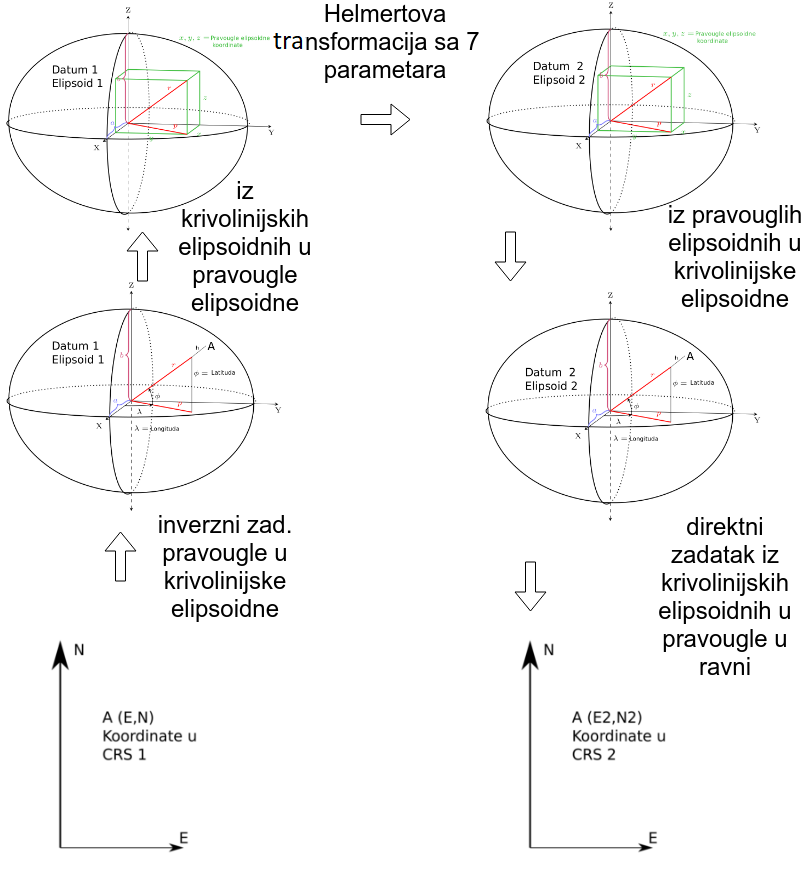
Kad su poznate koordinate u projekciji i definisan koordinatni referentni sistem, onda je moguće transformisati koordinate iz jednog koordinatnog referentnog sistema u drugi, Slika 2.23.

Slika 2.23: Shematski prikaz transformacije iz jednog koordinatnog sistema u projekciji u drugi.

2.7 Uvod u PROJ biblioteku

Biblioteka PROJ ili ranije poznata kao PROJ.4 trenutno raspolaže trima funkcionalnostima za transformaciju koordinata i geodetsko računanje:

  • proj/invproj – direktna i inverzna kartografska projekcija,
  • cs2cs – konverzija između koordinatnih sistema (geografskih ili u projekciji),
  • geod/invgeod – direktna i inverzna geodetska računanja.

Biblioteka PROJ.4 (PROJ contributors 2023) razvijena je početkom 1980. godine kao RATFOR program ((RATional FORtran, programski jezik)) gde većina kodova potiče od GCTP (Geological Survey’s General Cartographic Transformation Package). Program PROJ.4 je rekodiran u C programskom jeziku kada je MAPGEN paket, čiji je sastavni deo program PROJ.4, transformisan u UNIX operativni sistem. U program su dodate mnoge nove projekcije. Biblioteka je zasnovana na radu Geralda Evendena, kasnije ju je održavao Frank Warmerdam, koji je i tvorac GDAL biblioteke, a sada je održava zajednica programera.

PROJ biblioteka dolazi sa MIT (Massachusetts Institute of Technology) licencom koja dozvoljava slobodnu upotrebu, kopiranje, menjanje sadržaja, podlicenciranje, prodaju uz uslov da se uključi izvorna licenca i dopuštenje.

Instalacija PROJ biblioteke zavisi od operativnog sistema, a u daljem tekstu će biti data kratka ilustracija korišćenja biblioteke. U samoj biblioteci su sadržani parametri mnogih elipsoida, kao i predefinisanih geodetskih datuma sa vrednostima parametara.

Koristeći PROJ.4 notaciju može se zadati bilo koji koordinatni referentni sistem, bez ograničenja da se koriste samo predefinisani datumi koji su sadržani u biblioteci, s tim što se datum zadaje u odnosu na WGS84. Treba napomenuti da je sa x označen pravac istoka, a sa y pravac severa, kao u matematici (suprotno od geodetske notacije).

+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel  +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m

Zadat je koordinatni referentni sistem u Gaus-Krigerovoj projekciji za Srbiju, sa sledećim parametrima:

 +proj=tmerc - Gaus-Kriger (Transverzalna merkatorova) projekcija,                  
 +lat_0=0 +lon_0=21 - koordinatni početak na elipsoidu,                            
 +k=0.9999 - razmera duž srednjeg meridijana,                                        
 +x_0=7500000 +y_0=0 - koord. početak u ravni karte pravac ist. i sev.                          
 +ellps=bessel - elipsoid                                                            
 +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 - 3 translacije, 3 rotacije, razmera u odnosu na WGS84 izražena u ppm (parts per milion)  
 +=m - jedinice metri.

Pored toga, koordinatni referentni sistem u PROJ.4 notaciji može se zadati i koristeći EPSG kod. EPSG Geodetic Parameter Dataset je kolekcija definicija koordinatnih referentnih sistema i parametara koji opisuju te referentne sisteme.

Na stranici http://spatialreference.org/ ili na http://epsg.io mogu se naći definicije koordinatnih referentnih sistema u više notacija: EPSG, proj4, WKT, GML, JSON,… Na slici (Slika 2.24) dat je primer za WGS84 koordinatni sistem koji ima EPSG kod 4326.

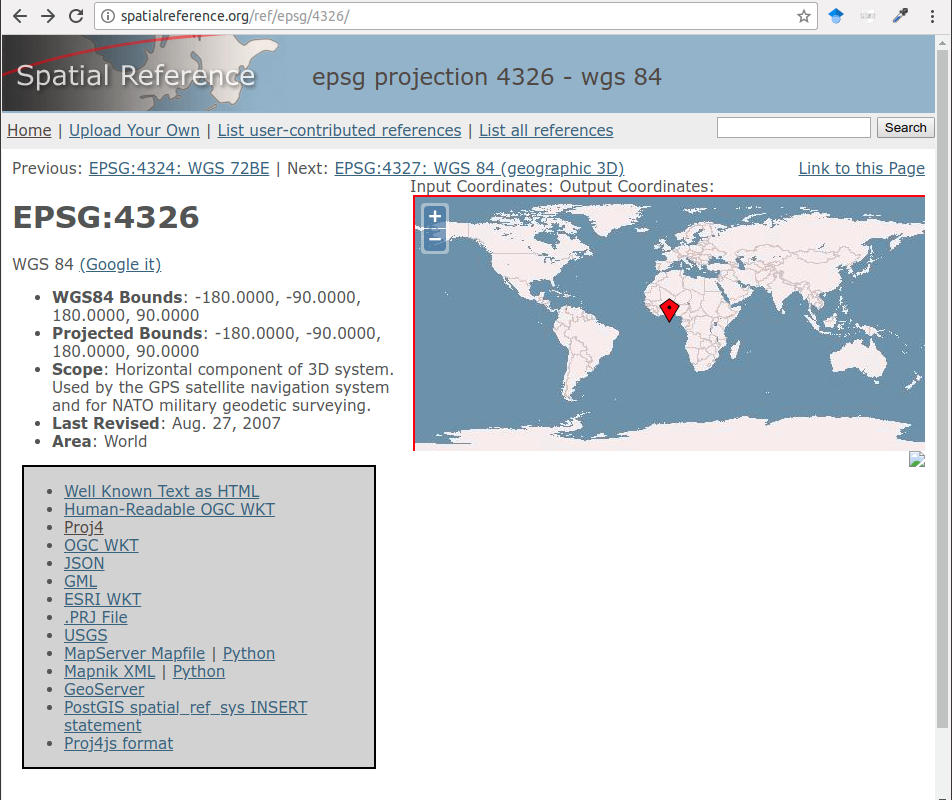
Slika 2.24: Primer korišćenja http://spatialreference.org/ sa mogućnostima preuzimanja parametara koordinatnih referentnih sistema u više notacija.

Primer direktnog računanja dat je za Gaus-Krigerovu projekciju:

proj +proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel  
21.33254 45.22587
   7526110.73   5009091.15

Pozivanjem proj komande očekuje se da korisnik unese elipsoidne koordinate preko terminala ili iz tekstualnog fajla da bi se dobile pravougle koordinate. Koristeći linux funkcionalnost komanda se može izvršiti i direktno iz jedne komande linije.

echo 21.33254 45.22587 | proj +proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel 
7526110.73  5009091.15

Kod inverznog kartografskog računanja neophodno je zadati i parametar -I, komanda očekuje ulazne pravougle koordinate i kao rezultat dobijaju se elipsoidne koordinate longituda i latituda. 

proj +proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel -I 
7526110.73 5009091.15
   21.332540       45.225870

Koordinatna transformacija iz jednog sistema u drugi ilustrovana je primerom konverzije iz Gaus-Krigerovog starog državnog sistema (elipsoid Bessel i datum Hermanskogel) u novi UTM koordinatni referentni sistem za Srbiju (elipsoid GRS80 sa ETRS89 datumom za Srbiju):

echo 7526110.73  5009091.15 | cs2cs +proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m +to +proj=utm +zone=34 +ellps=GRS80 +towgs84=0.26901,0.18246,0.06872,-0.01017,0.00893,-0.01172,0.04 +units=m
525672.87   5008094.39 42.46

Dat je i primer transformacije iz Gaus-Krigera za Srbiju u WGS84, gde je WGS84 zadat EPSG kodom, a detalji o funkciji se mogu naći na url adresi: http://proj4.org/apps/cs2cs.html.

echo 7526110.73  5009091.15 | cs2cs +proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m +to +init=epsg:4326 -f %12.6f
   21.327021       45.225867    42.986502

U 2018. godini, nakon uspešne inicijative GDAL Coordinate System Barn Raising, brojne kompanije koje su profitirale od širokog spektra geoprostornog softvera otvorenog koda podržale su razvoj modernijeg i zrelijeg sistema transformacije koordinata. Tokom nekoliko godina, PROJ.4 je evoluirao kroz verzije 5, 6, 7, 8 i 9 i stoga je preimenovan u PROJ.

Lista novina u PROJ biblioteci data je taksativno (Pebesma and Bivand 2023):

  • iako se PROJ.4 notacija i dalje može koristiti za inicijalizaciju koordinatnih referentnih sistema, neki koordinatni sistemi se ne mogu predstaviti koristeći ovu notaciju, novi format koji zamenjuje PROJ4 za zapis koordinatnih referentnih sistemaje WKT-2 (opisan u sledećem odeljku);

  • WGS84 kao centralni referentni sistem nije obavezno koristiti, transformacije koordinata više ne moraju da prolaze kroz određeni datum;

  • postoji više putanja konverzije ili transformacije (tzv. piplines) za prelazak sa KRS A na KRS B i mogu sadržati i informacije o odgovarajućoj tačnosti transformacije; PROJ će podrazumevano koristiti najprecizniji, ali je moguća korisnička kontrola;

  • moguće je ulančavati proizvoljan broj elementarnih operacija transformacije, uključujući zamenu osa i transformacije jedinica;

  • gridovani datumi, kojih je sada mnogo više, više se ne distribuiraju u biblioteci, već su dostupni iz mreže za isporuku sadržaja (CDN); PROJ omogućava mrežni pristup gridovanim datumima, ali i preuzimanje samo delova grida koji su zaista potrebni, čuvajući ih u keš memoriji ili u stalnoj memoriji korisnika za buduću upotrebu;

  • transformacije koordinata dobijaju podršku za epohe, transformacije zavisne od vremena (i otuda: četvorodimenzionalne koordinate, uključujući izvorno i ciljno vreme);

  • skup datoteka sa registrovanim koordinatnim referentnim sistemima skladišti se u SQLite bazi podataka;

  • redosled geodetskih koordinata je određen u samoj definiciji koordinatnog referentnog sistema, ne forsira se obavezan redosled geodetska dužina pa širina.

Lista svih podržanih projekcija data je na adresi https://proj.org/en/9.2/operations/projections/index.html.

Biblioteka PROJ je implementirana u mnogim GIS softverima i može se jednostavno koristiti kroz grafički interfejs. Takođe, PROJ biblioteka je implementirana u R-u, Pythonu i mnogim drugim programskim jezicima.

2.8 WKT-2

WKT-2 je sintaksa za definisanje i opis koordinatnih referentnih sistema definisana kao OGC standard (Lott 2015). Sintaksa WKT-2 se može koristiti za definisanje sledećih koordinatnih referentnih sistema:

Koordinatni referentni sistem EPSG:4326 koji je u proj4 notaciji ima sledeći zapis:

+proj=longlat +datum=WGS84 +no_defs +type=crs

Dok isti koordinatni sistem ima detaljniji zapis u WKT-2 notaciji:

GEOGCRS["WGS 84",
    ENSEMBLE["World Geodetic System 1984 ensemble",
        MEMBER["World Geodetic System 1984 (Transit)"],
        MEMBER["World Geodetic System 1984 (G730)"],
        MEMBER["World Geodetic System 1984 (G873)"],
        MEMBER["World Geodetic System 1984 (G1150)"],
        MEMBER["World Geodetic System 1984 (G1674)"],
        MEMBER["World Geodetic System 1984 (G1762)"],
        MEMBER["World Geodetic System 1984 (G2139)"],
        ELLIPSOID["WGS 84",6378137,298.257223563,
            LENGTHUNIT["metre",1]],
        ENSEMBLEACCURACY[2.0]],
    PRIMEM["Greenwich",0,
        ANGLEUNIT["degree",0.0174532925199433]],
    CS[ellipsoidal,2],
        AXIS["geodetic latitude (Lat)",north,
            ORDER[1],
            ANGLEUNIT["degree",0.0174532925199433]],
        AXIS["geodetic longitude (Lon)",east,
            ORDER[2],
            ANGLEUNIT["degree",0.0174532925199433]],
    USAGE[
        SCOPE["Horizontal component of 3D system."],
        AREA["World."],
        BBOX[-90,-180,90,180]],
    ID["EPSG",4326]]

2.9 Primeri računanja na elipsoidu koristeći sf i s2 paket

Sračunati pravougle elipsoidne koordinate na WGS84 za tačku GRF, zadatu sa geodetskom dužinom \(\lambda=20.4759749\), i širinom \(\varphi=44.8057705\) u stepenima, koristeći sf paket (Pebesma 2018b).

library(sf)
p = st_as_sfc("POINT(20.4759749 44.8057705)", crs = 4326) 
p = st_transform(p, "+proj=geocent")
p[[1]]
# POINT Z (4246439 1585649 4472060)

Transformisati tačku GRF(lon=20.4759749, lat=44.8057705)) sa WGS84 na Beselov elipsoid sa datumom Hermanskogel.
Izraziti razliku geodetskih koordinata u sekundama. Koliko bi se približno razlikovala pozicija ovih tačaka da su na istom elipsoidu (aproksimirati elipsoid loptom)?

library(sf)
options(digits = 12)
pw = st_as_sfc("POINT(20.4759749 44.8057705)", 
     crs = 4326) 
pb = st_transform(pw, 
        crs="+proj=longlat +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m +type=crs")
pb[[1]] # koordinate na Beselu datum Hermanskogel
# POINT (20.4813687832 44.8057493124)

round( (as.numeric( pb[[1]] ) - as.numeric( pw[[1]] ) )*3600 ,1 )
# [1] 19.4 -0.1

# Zamislimo da su koordinate na istom elipsoidu.
# Koliko je jedna sekunda metara kružnog luka lopte?
# Ugao u radijanima kod meridijana  df = l/R => l=R*df
# Kod paralele dl= l/Rcos(fi) => l=R*cos(fi)*dl

l= 6377000* cos(44.8057705*pi/180)* (19.4/3600 *pi/180)

# Da su ove koordinate na istom elipsoidu razlikovale bi se približno za 
round(l,1) # m
# [1] 425.5

Sračunati dužinu geodetske linije na WGS84 elipsoidu, od Beograda (lon=20.455727, lat=44.800153) do Tokija (lon=139.767118, lat= 35.679207).

library(sf)
options(digits = 12)
bg = st_as_sfc("POINT(20.455727 44.800153)", crs = 4326) 
tk = st_as_sfc("POINT(139.767118 35.679207)", crs = 4326) 
sf_use_s2(TRUE) # koristi elipsoidna računanja
st_distance(bg,tk)
# Units: [m]
#               [,1]
# [1,] 9184644.51421
# u km napomena koristimo pipe karakter |> i paket units
st_distance(bg,tk)|> units::set_units(km)
# Units: [km]
#               [,1]
# [1,] 9184.64451421

Sračunati dužinu vektora između tačaka Beograd (lon=20.455727, lat=44.800153) i Tokijo (lon=139.767118, lat= 35.679207) koristeći elipsoidne pravougle koordinate. Uporediti dužinu ovog vektora u prostoru sa pre dobijenom dužinom geodetske linije koja je kriva linija na elipsoidu.

library(sf)
options(digits = 12)
bg = st_as_sfc("POINT(20.455727 44.800153)", crs = 4326) 
tk = st_as_sfc("POINT(139.767118 35.679207)", crs = 4326)

(bgXYZ = st_transform(bg, "+proj=cart +ellps=WGS84"))
# Geometry set for 1 feature 
# Geometry type: POINT
# Dimension:     XYZ
# Bounding box:  xmin: 4247411.12991 ymin: 1584302.22106 xmax: 4247411.12991 ymax: 1584302.22106
# z_range:       zmin: 4471616.94533 zmax: 4471616.94533
# Projected CRS: +proj=cart +ellps=WGS84
# POINT Z (4247411.12991 1584302.22106 4471616.94...
(tkXYZ = st_transform(tk, "+proj=cart +ellps=WGS84"))
# Geometry set for 1 feature 
# Geometry type: POINT
# Dimension:     XYZ
# Bounding box:  xmin: -3959765.51423 ymin: 3350158.57583 xmax: -3959765.51423 ymax: 3350158.57583
# z_range:       zmin: 3699337.17349 zmax: 3699337.17349
# Projected CRS: +proj=cart +ellps=WGS84
# POINT Z (-3959765.51423 3350158.57583 3699337.1...

dXYZ = as.numeric(bgXYZ[[1]]) - as.numeric(tkXYZ[[1]])

d= sqrt(dXYZ[1]^2 +dXYZ[2]^2 +dXYZ[3]^2)

round(d,2) #m
# [1] 8430445.61

round(d/1000,2) #km
# [1] 8430.45

Koristeći s2 (Dunnington, Pebesma, and Rubak 2023) paket sračunati površinu kopnenih masa i pokrivenost Zemlje morima i okeanima. Sve sračunate površine su površine na elipsoidu, ne u projekciji.

options(digits = 12)
library(sf)
library(s2)
# Warning: package 's2' was built under R version 4.2.3
# preuzmimo poligone ili multipoligone granica svih država iz s2 paketa
co = s2::s2_data_countries()
plot(co)


head(co)
# <geodesic s2_geography[6] with CRS=OGC:CRS84>
# [1] POLYGON ((61.2108171 35.6500723, 60.8031934 34.4041019, 60.5284298 33.676446, 60.9637004 33.5288323, 60.5360779 32.9812688...       
# [2] MULTIPOLYGON (((16.3265284 -5.8774704, 13.3755974 -5.8642412, 13.0248694 -5.9843889, 12.7351713 -5.9656821, 12.3224317 -6.1000925...
# [3] POLYGON ((20.5902474 41.8554042, 20.52295 42.21787, 20.2837545 42.3202595, 20.0707 42.58863, 19.8016134 42.5000935...               
# [4] POLYGON ((51.5795187 24.2454971, 51.6177076 24.0142193, 52.0007333 23.0011545, 55.006803 22.4969475, 55.2083411 22.70833...         
# [5] MULTIPOLYGON (((-65.5 -55.2, -65.05 -54.7, -66.45 -54.45, -67.75 -53.85, -68.25 -53.1...                                            
# [6] POLYGON ((43.5827458 41.0921433, 43.7526579 40.7402009, 43.6564364 40.253564, 44.4000086 40.0050003, 44.7939897 39.7130026...

# sračunati površinu celu kopnenu masu
# napravimo prvo uniju svih država
kopno = s2_union_agg(co)

plot(kopno)


# km2
s2_area(kopno) / 1000000
# [1] 147255540.467

# sračunati odnos okeana i cele površine
g = as_s2_geography(TRUE) #ceo elipsoid
okeani = s2_difference(g, kopno) # okeani

s2_area(okeani) / s2_area(g)
# [1] 0.711301048574
Barnes, Richard. 2020. “Webglobe: 3D Interactive Globes.” https://CRAN.R-project.org/package=webglobe.
Dunnington, Dewey, Edzer Pebesma, and Ege Rubak. 2023. “S2: Spherical Geometry Operators Using the S2 Geometry Library.” https://CRAN.R-project.org/package=s2.
Hengl, Tomislav, Pierre Roudier, Dylan Beaudette, and Edzer Pebesma. 2015. “plotKML: Scientific Visualization of Spatio-Temporal Data” 63. https://www.jstatsoft.org/v63/i05/.
Hijmans, Robert J. 2022. “Geosphere: Spherical Trigonometry.” https://CRAN.R-project.org/package=geosphere.
Jovanović, Velibor. 1984. Matematička Kartografija. VGI.
Lott, Roger. 2015. “Geographic Information-Well-Known Text Representation of Coordinate Reference Systems.” Open Geospatial Consortium. http://docs.opengeospatial.org/is/12-063r5/12-063r5.html.
Pebesma, Edzer. 2018a. Sf: Simple Features for R. https://CRAN.R-project.org/package=sf.
———. 2018b. “Simple Features for r: Standardized Support for Spatial Vector Data” 10. https://doi.org/10.32614/RJ-2018-009.
Pebesma, Edzer, and Roger Bivand. 2023. “Spatial Data Science,” March. https://doi.org/10.1201/9780429459016.
PROJ contributors. 2023. PROJ Coordinate Transformation Software Library. Open Source Geospatial Foundation. https://doi.org/10.5281/zenodo.5884394.
Varga, Matej. 2021. “Geometrijska geodezija: Glavni geodetski zadatci, transformacije i konverzije koordinata, Priručnik algoritama i numeričkih primjera.” Unpublished. https://doi.org/10.13140/RG.2.2.17926.70725.