
6 Azimutne projekcije
Treća važna familija kartografskih projekcija su azimutne (ili perspektivne, zenitne) projekcije. Kod ovih projekcija preslikavanje se vrši direktno na ravan koja je tipično tangirajuća na različite tačke Zemljine lopte kao što su polovi, tačka na Ekvatoru ili tačka u centru prodručja preslikavanja. Glavne varijacije uključuju polarne, ekvatorijalne ili kose kad ravan tangira tačku koja je najčešće sredina područja projiciranja. Mogu biti i sekuće, gde ravan seče loptu ili elipsoid po unapred zadatoj liniji, Slika 6.1.
Neke od azimutnih projekcija su perspektivne, dok druge nisu. Perspektivne cilindrične i konusne projekcije se ređe koriste (formule izvodimo analitički kao što je pokazano u prethodnim poglavljima), perspektivne azimutne projekcije imaju čestu upotrebu zbog svojih svojstava da se tačke linearno projiciraju sa Zemljine lopte (ili elipsoida) na ravan, za sve azimutne projekcije formule se mogu izvesti i na analitički način.
Kod polarnih azimutnih stereografskih projekcija (centar projiciranja u suprotnom polu) meridijani i paralele istovremeno su i glavni pravci, jer je mreža meridijana i paralela ortogonalna kao i na originalnoj površi. Meridijani su prave linije, a paralele su krugovi, Slika 6.2.

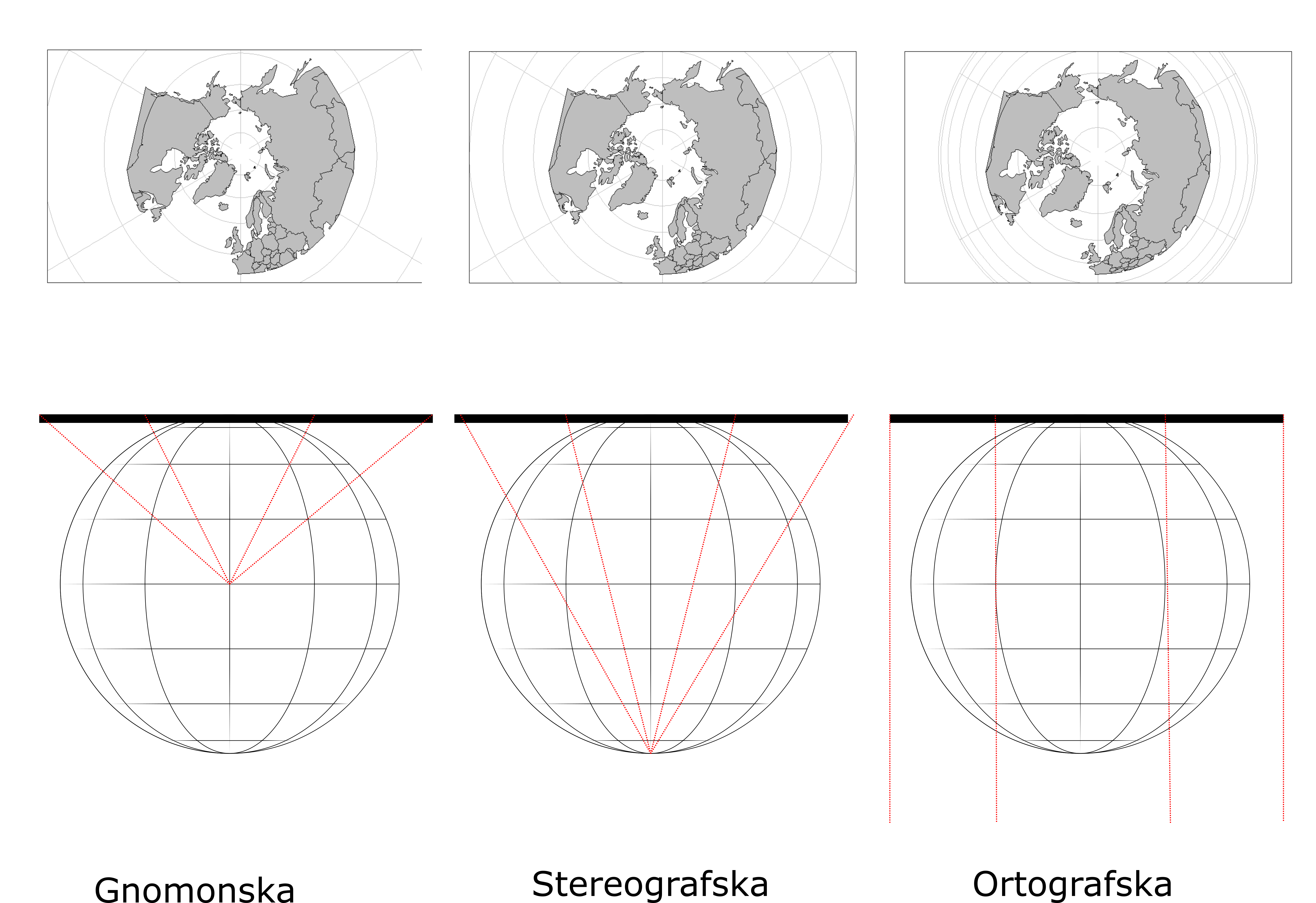
Prema položaju tačke projiciranja azimutne projekcije se dele na (Slika 6.3): gnomonske (centar projiciranja u centru lopte), stereografske (centar projiciranja u suprotnom polu) i ortografske (centar projiciranja u beskonačnosti).
6.1 Gnomonska projekcija
Gnomonska projekcija je prava perspektiva (tačke se linearno projiciraju sa Zemljine lopte (ili elipsoida) na ravan). Tačka projiciranja je centar Zemlje, a geometrija prostornih podataka se projicira na tangentnu ravan. Svi veliki krugovi sa sfere (geodetske linije), ne samo oni koji prolaze kroz centar sfere, prikazani su kao prave linije. Kod preslikavanja sa elipsoida na ravan geodetske linije se preslikavaju kao približno prave linije.
Osobine (Snyder (1987)):
- Svi meridijani su prave linije.
- Sve paralele osim Ekvatora i polova su elipse, parabole ili hiperbole.
- U pogledu deformacija nije ni konformna ni ekvivalentna.
- Svi veliki krugovi su prikazani kao prave linije.
- Manje od jedne hemisfere može biti prikazano oko datog centra.
- Bez deformacija samo u centru, tački gde ravan tangira sferu.
- Deformacije se brzo povećavaj udaljavnjemu od centra.
- Pravci iz centralne tačke se preslikavaju bez deformacija.
- Koristi se samo u sfernom obliku.
Izvanredna (i jedina korisna) karakteristika Gnomonske projekcije proizilazi iz činjenice da svaki luk velikog kruga, najkraća udaljenost između bilo koje dve tačke na površini sfere, leži u ravni koja prolazi kroz centar globusa (sfere). Dakle, svi lukovi velikog kruga projektuju se kao prave linije na ovoj projekciji. Deformacija dužine geodetske linije je velika, ali je njen pravac precizan za preslikavanje sa sfere (ne i za elipsoid kad je pravac približan).
Formule možemo jednostavno izvesti (Slika 6.4).
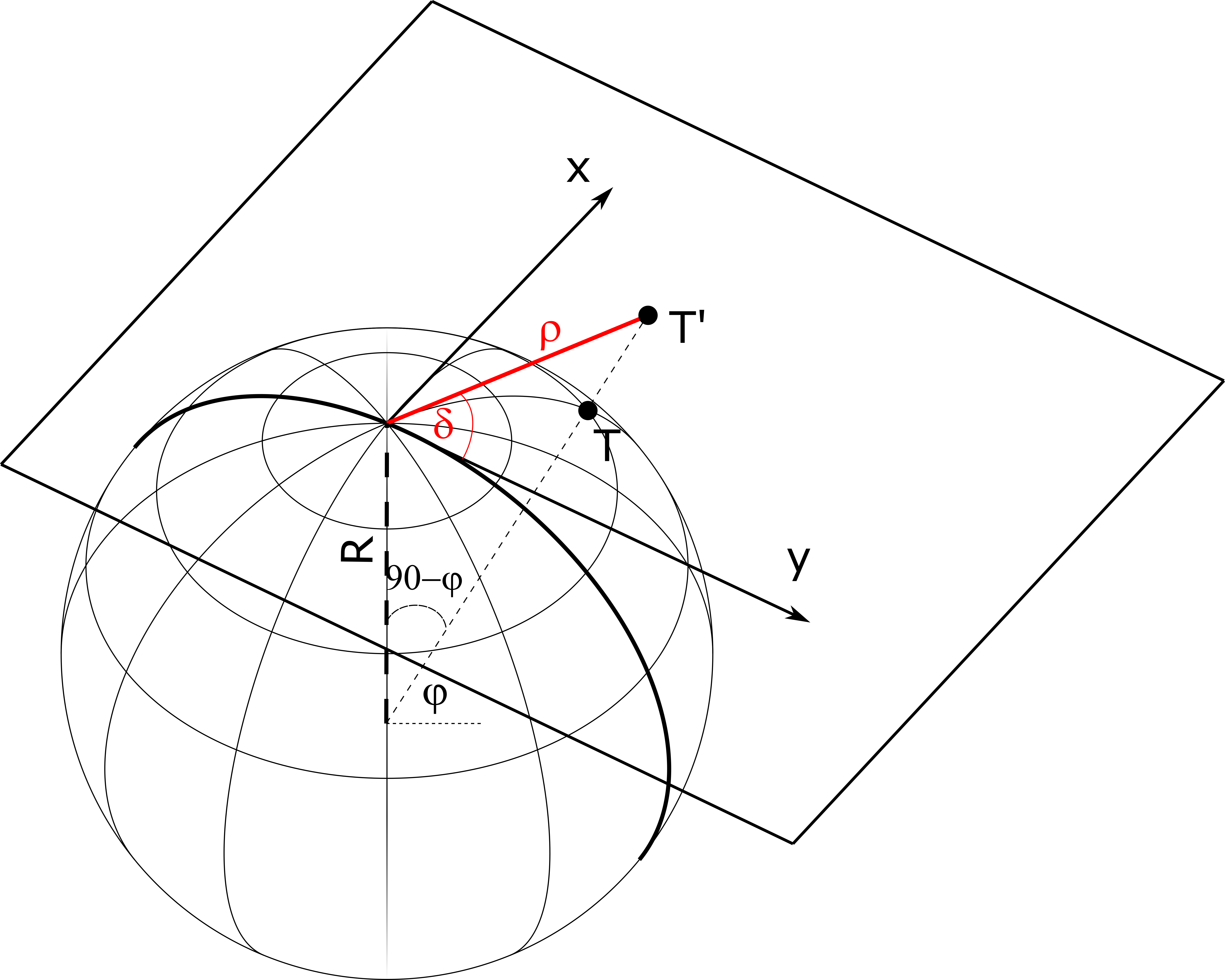
Polarne koordinate imaju oblik: \[ \begin{aligned} & \rho=R \cot \varphi \\ & \delta=\lambda-\lambda_0 \end{aligned} \]
Pravougle koordinate su za Severni pol:
\[ \begin{aligned} & x=R \cot \varphi \sin \left(\lambda-\lambda_0\right) \\ & y=-R \cot \varphi \cos \left(\lambda-\lambda_0\right) \end{aligned} \]
Pravougle koordinate su za Južni pol:
\[ \begin{aligned} & x=-\mathrm{R} \cot \varphi \sin \left(\lambda-\lambda_0\right) \\ & y=R \cot \varphi \cos \left(\lambda-\lambda_0\right) \end{aligned} \]
Polarne koordinate za tangirajuću tačku na Ekvatoru su:
\[ \begin{aligned} & \rho=-R \cot \varphi \\ & \delta=\pi-\lambda+\lambda_0 \end{aligned} \] Pravougle koordinate za tangirajuću tačku na Ekvatoru su:
\[ \begin{aligned} & x=R \tan \left(\lambda-\lambda_0\right) \\ & y=R \tan \varphi / \cos \left(\lambda-\lambda_0\right) \end{aligned} \]
Za bilo koju tangirajuću tačku (\(|\varphi_0|<90\)), Slika 6.5, imamo da je centralna tačka obeležena sa Z, kroz tu tačku prolazi i almukantarat koji ima zenitno odstojanje \(z\).

Tada važi opšti oblik:
\[ \begin{aligned} & \rho=R \tan z\\ & \delta=a_z \quad, a_z \quad \text{je zenitni azimut} \\ & \mu_z=1 / \cos ^2 z \quad, \quad \text{linearna razmera u pravcu vertikala} \\ & \mu_a=1 / \cos z \quad , \quad \text{linearna razmera u pravcu almukantarata} \end{aligned} \] \[ \begin{aligned} & x=R \mu_a \cos \varphi \sin \left(\lambda-\lambda_0\right) \\ & y=R \mu_a\left[\cos \varphi_0 \sin \varphi-\sin \varphi_0 \cos \varphi \cos \left(\lambda-\lambda_0\right)\right] \end{aligned} \]
\[ \begin{aligned} & \sin z \cos a_z=\sin \varphi \cos \varphi_0-\sin \varphi_0 \cos \varphi \cos \lambda \\ & \sin z \sin a_z=\sin \lambda \cos \varphi \\ & \cos z=\sin \varphi_o \sin \varphi+\cos \varphi_0 \cos \varphi \cos \lambda \end{aligned} \]
Inverzni zadatak za Gnomonsku projekciju:
\[ \varphi=\arcsin \left[\cos z \sin \varphi_0+\left(y \sin z \cos \varphi_0 / \rho\right)\right] \]
Za \(\varphi_0=90^o\) (Severni pol):
\[ \lambda=\lambda_0+\arctan [x /(-y)] \]
Za \(\varphi_0=-90^o\) (Južni pol):
\[ \lambda=\lambda_0+\arctan (x / y) \]
Za bilo koje \(\varphi_0\) različito od \(90^o\) i \(-90^o\) :
\[ \lambda=\lambda_0+\arctan \left[x \sin z /\left(\rho \cos \varphi_0 \cos z-y \sin \varphi_0 \sin z\right)\right] \]
Gde su:
\[ \begin{aligned} & \rho=\left(x^2+y^2\right)^{1 / 2} \\ & z =\arctan (\rho / R) \end{aligned} \]
Kod Gnomonske projekcije udaljavanjem od tangentne tačke (centralne tačke) deformacije dužina, površina i uglova rastu, Slika 6.6. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 300 km na sferi (R=6377 km) i odgovarajuće površine u projekciji. Sa slike je očigledno da je prvi glavni pravac u pravcu meridijana, dok je drugi glavni pravac u pravcu paralele.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(-180,180, by=60)
f = c(20, 30, 40, 50, 60, 70, 90) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +a=6377000 +b=6377000") #sfr R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000, radius=6377000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf, radius=6377000)
# transformacija poligona elipsi u Gn projekciji
gn_crs = "+proj=gnom +lat_0=90 +lon_0=0 +a=6377000 +b=6377000"
tissot.gn <- st_transform(tissot.sf, gn_crs)
# površine u projekciji
tissot.gn$a_proj <- st_area(tissot.gn)
# odnos površina u projekciji i na sferi
tissot.gn$p <- tissot.gn$a_proj/tissot.gn$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# izdvojimo okvirno severni deo lopte
sf_use_s2(FALSE)
north <- st_crop(world, xmin = -180, xmax = 180,
ymin = 20, ymax = 90)
sf_use_s2(TRUE)
north_gn = st_transform(north, crs = gn_crs)
ll = st_centroid(tissot.gn)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(north_gn), graticule = TRUE,
col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.gn),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.gn$p,1)) ,col='red' , cex = 0.8)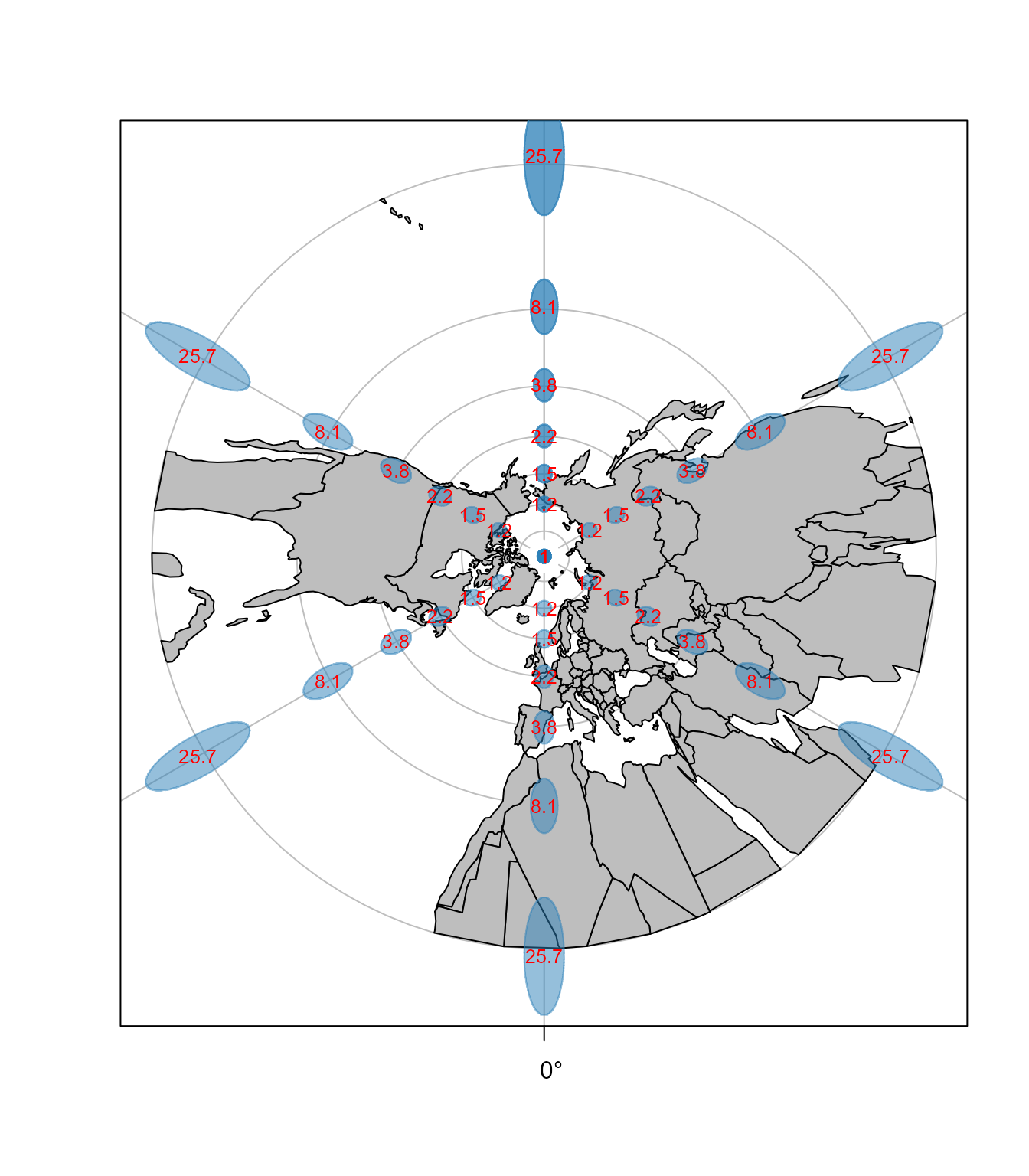
Gnomonska projekcija tangentna tačka je definisana u Beogradu, udaljavanjem od tangentne tačke deformacije dužina, površina i uglova rastu, Slika 6.7. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 300 km na sferi (R=6377 km) i odgovarajuće površine u projekciji. Lako je uočiti sa karte da mreža meridijana i paralela u ovoj varijanti Gnomonske projekcije nije ortogonalna.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(10,90, by=30)
f = c(20, 30, 45, 60, 70, 90) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +a=6377000 +b=6377000")#sfr. R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000, radius=6377000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf, radius=6377000)
# transformacija poligona elipsi u Gn projekciji
gn_crs = "+proj=gnom +lat_0=44.800153 +lon_0=20.455727 +a=6377000 +b=6377000"
tissot.gn <- st_transform(tissot.sf, gn_crs)
# površine u projekciji
tissot.gn$a_proj <- st_area(tissot.gn)
# odnos površina u projekciji i na sferi
tissot.gn$p <- tissot.gn$a_proj/tissot.gn$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# izdvojimo okvirno severni deo lopte
sf_use_s2(FALSE)
north <- st_crop(world, xmin = 0, xmax =90,
ymin = 20, ymax = 90)
sf_use_s2(TRUE)
north_gn = st_transform(north, crs = gn_crs)
ll = st_centroid(tissot.gn)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(north_gn), graticule = TRUE,
col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.gn),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.gn$p,1)) ,col='red' , cex = 0.8)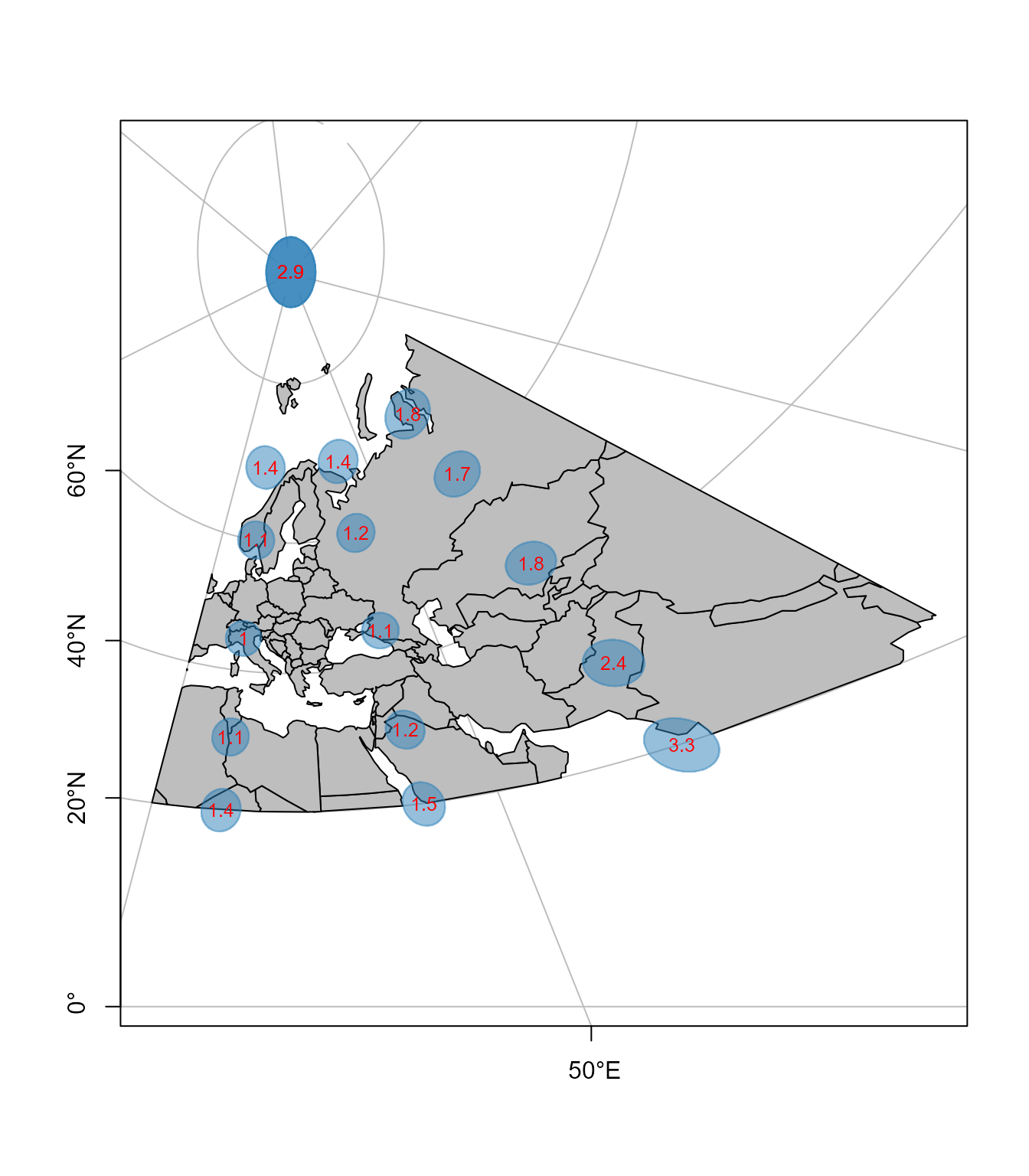
6.2 Stereografska projekcija
Stereografska projekcija je prava perspektiva u sfernom obliku (tačke se linearno projiciraju sa Zemljine lopte na ravan), sa projekcionim centrom na površini sfere u tački tačno suprotnoj od tačke tangente za ravan, ili suprotno centru projekcije, čak i ako je ravan sekantna. Ova projekcija je konformna za sferu ili elipsoid. Elipsoidni oblik nije istinski perspektivan, formule se izvode analitički.
Osobine (Snyder (1987)):
- Konformna je u pogledu deformacija.
- Centralni meridijan i određena paralela (ako je prikazana) su prave linije.
- Svi meridijani na polarnom aspektu i Ekvator na ekvatorijalnom aspektu su prave linije.
- Svi ostali meridijani i paralele prikazani su kao lukovi krugova.
- Perspektivna projekcija za sferu.
- Pravci iz centra projekcije su tačni (osim na elipsoidnim kosim ili ekvatorijalnim).
- Razmer dužina i površina se povećava udaljavanjem od centra projekcije.
- Tačka nasuprot centru projekcije ne može da se kartira.
- Koristi se za polarne karte i razne specijalne karte.
Univerzalna polarna stereografska projekcija (UPS (Universal Polar Stereographic)) koristi se za UTM koordinatni sistem u polarnim oblastima, i to od širine \(83^o30' N\) i od \(79^o30' S\). Kod UPS projekcije se koristi sekuća ravan. Linearna razmera na svakom polu je podešena na 0.994 tako da je geodetska širina standardne paralele (\(c=1\)), \(\varphi_0=81.11451786859362545\) (što je oko \(\varphi_0=81^o 06' 52.3''\) ) severno i za Južni pol, južno, Slika 6.8. Koordinatni početak u ravni definisan je koordinatama (false esating = 2000000, false nothing = 2000000).
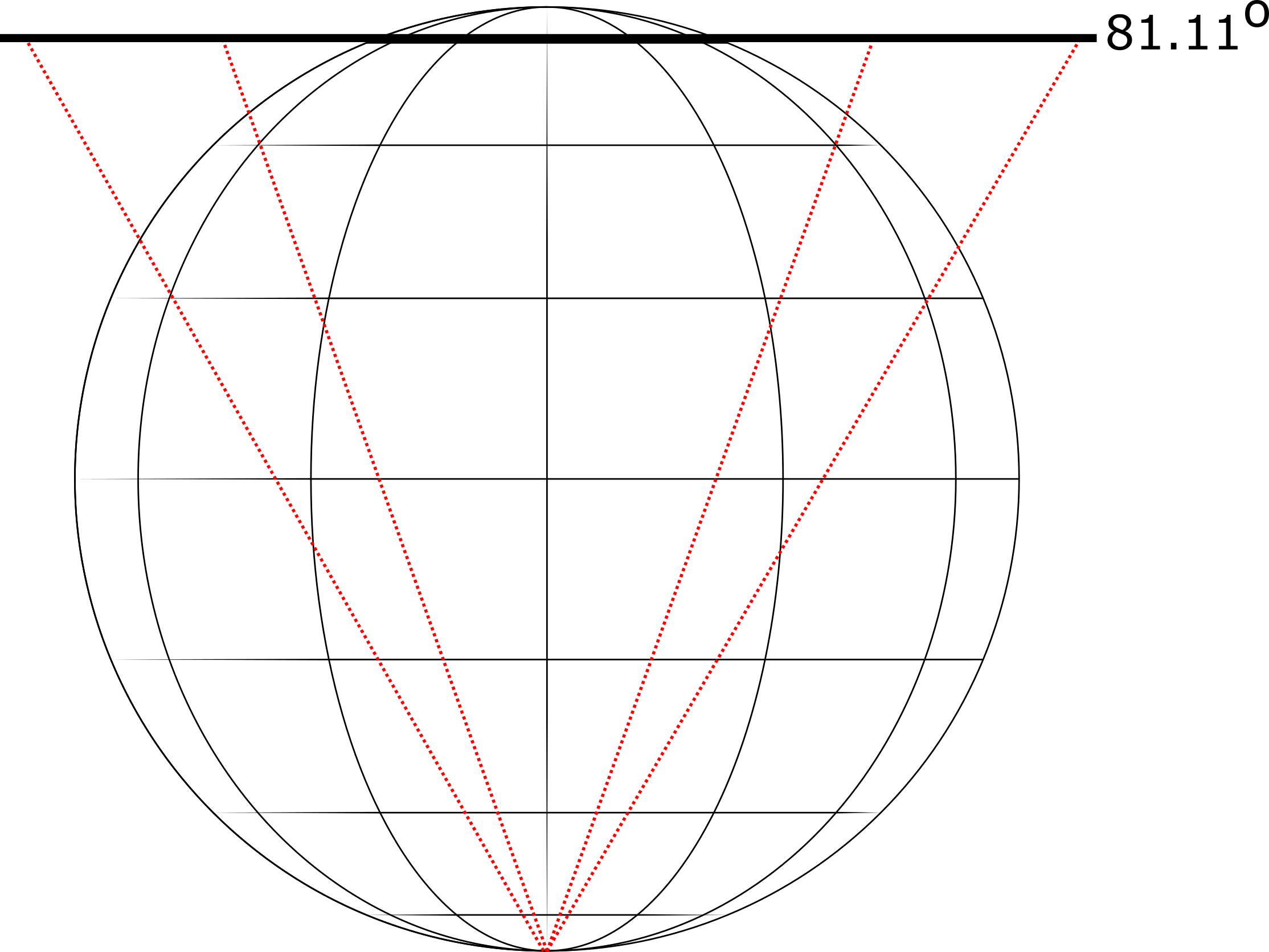
Jednačine UPS projekcije za preslikavanje sa elipsoida date su sledećim formulama (Hager et al. 1989):
\[ \begin{aligned} & C_0=\frac{2 a}{\left(1-e^2\right)^{1 / 2}}\left[\frac{1-e}{1+e}\right]^{e / 2} \\ & \tan \frac{z}{2}=\left[\frac{1+e \sin \varphi}{1-e \sin \varphi}\right]^{e / 2} \tan \left(\frac{\pi}{4}-\frac{\varphi}{2}\right) \\ & \rho(\varphi)=0.9994 C_0 \tan \frac{z}{2} \end{aligned} \]
Pravougle koordinate za Severni pol:
\[ \begin{aligned} & x=N=2000000-\rho(\varphi) \cos \lambda \\ & y=E=2000000+\rho(\varphi) \sin \lambda \end{aligned} \]
Pravougle koordinate za Južni pol:
\[ \begin{aligned} & x=N=2000000+ \rho(\varphi) \cos \lambda \\ & y=E=2000000+ \rho(\varphi) \sin \lambda \end{aligned} \]
Linearna razmera data je formulom:
\[ c=m=n= \frac{\rho(\varphi)} { N(\varphi)cos(\varphi)} \] Gde je \(N\) poluprečnik krivine prvog vertikala, \(N=N(\varphi)=\frac{a}{\sqrt{1-e^2 \sin ^2 \varphi}}\).
Inverzni zadatak kod UPS projekcije:
\(\lambda=\operatorname{arccot} \frac{-\Delta N}{\Delta E} \quad\) za Severni pol. \(\lambda=\operatorname{arccot} \frac{\Delta N}{\Delta E} \quad\) za Južni pol.
Gde je:
\(\Delta N = N - N_0 = N - 2000000\) \(\Delta E = E - E_0 = E - 2000000\)
Kod računanja širine prvo se sračuna \(\rho\):
\[ \rho=\left|\frac{\Delta E}{\sin \lambda}\right| \quad \text { gde } \Delta E \neq 0 \]
ili
\[ \rho=\left|\frac{\Delta N}{\cos \lambda}\right| \quad \text { gde } \Delta N \neq 0 \]
Potom:
\[ \tan \frac{z}{2}=\frac{\rho}{\left(c_0 C_0\right)} = \frac{\rho}{\left(0.9994 C_0\right)} \]
Dalje je:
\[ \chi=\frac{\pi}{2}-z \]
Konačno imamo formulu za geodetsku širinu u obliku:
\[ \varphi=\chi+\bar{A} \sin 2 \chi+\bar{B} \sin 4 \chi+\bar{C} \sin 6 \chi+\bar{D} \sin 8 \chi \]
Gde su:
\[ \begin{aligned} & \bar{A}=\frac{e^2}{2}+\frac{5 e^4}{24}+\frac{e^6}{12}+\frac{13 e^8}{360} \\ & \bar{B}=\frac{7 e^4}{48}+\frac{29 e^6}{240}+\frac{811 e^8}{11520} \\ & \bar{C}=\frac{7 e^6}{120}+\frac{81 e^8}{1120} \\ & \bar{D}=\frac{4279 e^8}{161280} \\ & e^2 = (prvi.\quad num.\quad eksc.\quad el.)^2 = \frac{a^2-b^2}{a^2} \end{aligned} \]
UPS projekcija je prikazana sa elipsama deformacija, Slika 6.8. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 300 km na elipsoidu i odgovarajuće površine u projekciji.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(-180,180, by=60)
f = c(20, 30, 40, 50, 60, 70, 90) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = 4326)
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na wgs84 (geometrija je skoro ista kao grs80)
sf_use_s2(FALSE) # koristi elipsoidna računanja
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u UPS projekciji
ups_crs = "+proj=ups"
tissot.ups <- st_transform(tissot.sf, ups_crs)
# površine u projekciji
tissot.ups$a_proj <- st_area(tissot.ups)
# odnos površina u projekciji i na sferi
tissot.ups$p <- tissot.ups$a_proj/tissot.ups$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# izdvojimo okvirno severni deo lopte
north <- st_crop(world, xmin = -180, xmax = 180,
ymin = 20, ymax = 90)
sf_use_s2(TRUE)
north_ups = st_transform(north, crs = ups_crs)
ll = st_centroid(tissot.ups)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(north_ups), graticule = TRUE,
col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.ups),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.ups$p,1)) ,col='red' , cex = 0.8)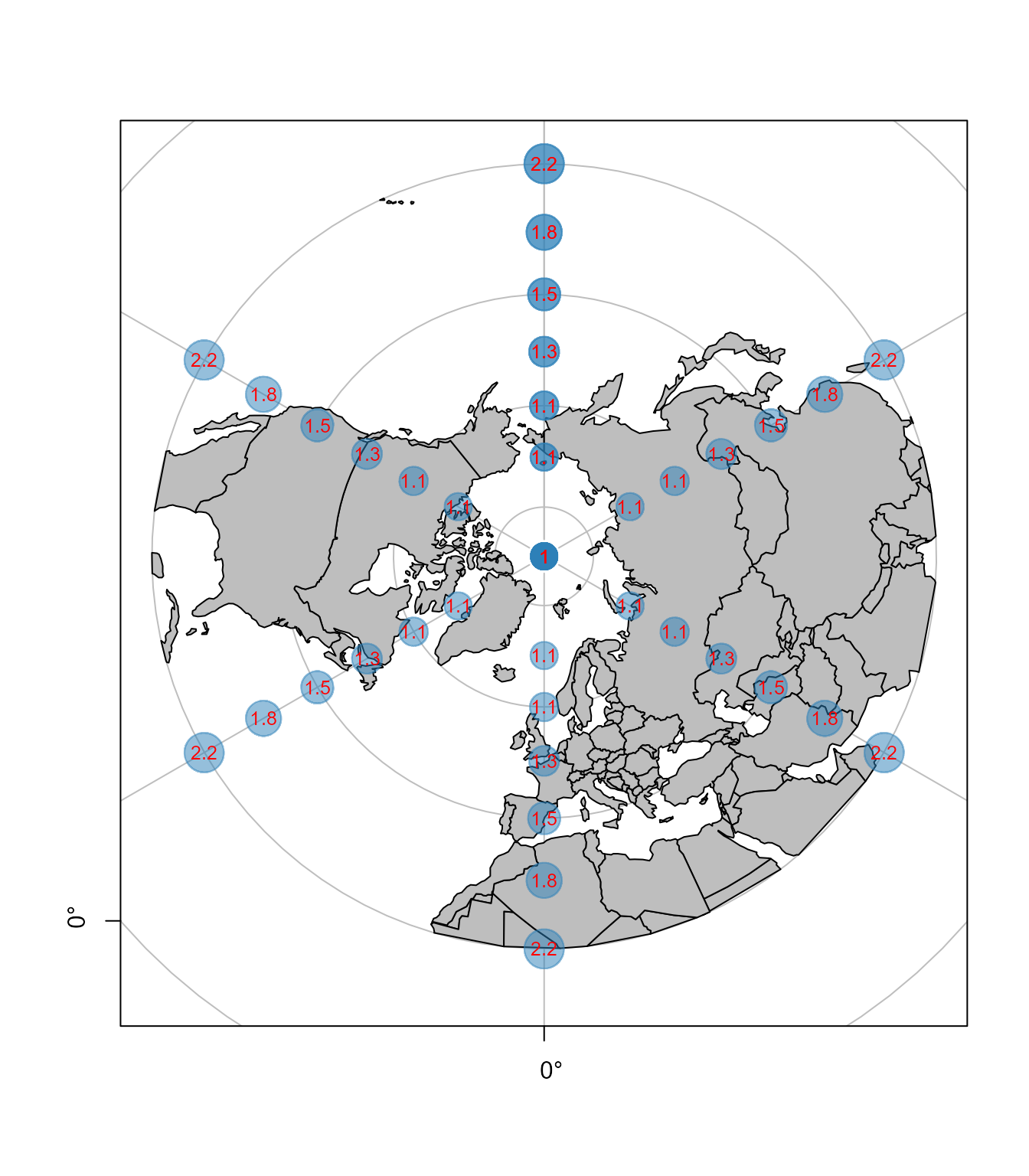
6.3 Ortografska projekcija
Ortografska projekcija je prava perspektiva, u kojoj je Zemlja projektovana sa beskonačne udaljenosti na ravan. Karte u ortografskoj projekciji izgledaju kao globus, naglašavajući na taj način oblik planete Zemlje.
Osobine (Snyder (1987)):
- Svi meridijani i paralele su elipse, krugovi ili prave linije.
- Uslovna je projekcija u pogledu deformacija.
- Izgledom veoma podseća na globus, jer je perspektivna projekcija sa beskonačne udaljenosti.
- Samo jedna hemisfera može biti prikazana istovremeno.
- Deformacije su značajne u blizini granica prikazane hemisfere.
- Bez deformacija samo u centru.
- Pravci iz centra (tangentne tačke) preslikavajuse se bez deformacija..
- Koristi se uglavnom za slikovne prikaze i za potrebe ilustracija.
- Koristi se samo u sfernom obliku
Formule za direktni zadatak:
\[ \begin{aligned} & x=R \cos \varphi \sin \left(\lambda-\lambda_0\right) \\ & y=R\left(\cos \varphi_0 \sin \varphi-\sin \varphi_0 \cos \varphi \cos \left(\lambda-\lambda_0\right)\right) \end{aligned} \] Inverzni zadatak:
\[ \begin{aligned} & \varphi=\arcsin \left(\cos z \sin \varphi_0+\frac{y \sin z \cos \varphi_0}{\rho}\right) \\ & \lambda=\lambda_0+\arctan \left(\frac{x \sin z}{\rho \cos z \cos \varphi_0-y \sin z \sin \varphi_0}\right) \end{aligned} \]
Gde je:
\[ \cos z=\sin \varphi_0 \sin \varphi+\cos \varphi_0 \cos \varphi \cos \left(\lambda-\lambda_0\right) \] \[ \begin{aligned} \rho & =\sqrt{x^2+y^2} \\ z & =\arcsin \frac{\rho}{R} \end{aligned} \]
Elipse deformacija u Ortografskoj projekciji, Slika 6.10. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 300 km na sferi (R=6377 km) i odgovarajuće površine u projekciji.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(-180,180, by=60)
f = seq(-90,90,by=15) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +a=6377000 +b=6377000") # sfera R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000, radius=6377000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf, radius=6377000)
# transformacija poligona elipsi u Ort projekciji
ort_crs = "+proj=ortho +lat_0=20 +lon_0=-10 +a=6377000 +b=6377000"
tissot.ort <- st_transform(tissot.sf, ort_crs)
# površine u projekciji
tissot.ort$a_proj <- st_area(tissot.ort)
# odnos površina u projekciji i na sferi
tissot.ort$p <- tissot.ort$a_proj/tissot.ort$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_ort = st_transform(world, crs = ort_crs)
ll = st_centroid(tissot.ort)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_ort), graticule = TRUE,
col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.ort),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.ort$p,1)) ,col='red' , cex = 0.8)
Izgled geodetske linije i loksodrome od Beograda do Tokija u Ortografskoj projekciji prikazan je na karti, Slika 6.11.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
library(geosphere)
library(ggplot2)
# Koordinate BG i TK
bg_coords <- c(20.455727, 44.800153)
tk_coords <- c(139.767118, 35.679207)
# sf format
bg <- st_point(bg_coords)
tk <- st_point(tk_coords)
# Geodetska linija paket geosphre
great_circle_line <- geosphere::greatCircle(bg_coords, tk_coords, n=1000)
# Loksodroma paket geosphre
azimut <- bearingRhumb(bg_coords, tk_coords)
duzL <- distRhumb(bg_coords, tk_coords)
rhumb_line <- destPointRhumb(bg_coords, azimut, d=round(duzL/1000) * 1:1000)
# sf format
ls1 = st_linestring(great_circle_line)
ls2 = st_linestring(rhumb_line)
lines = st_sfc(ls1,ls2, crs ="+proj=longlat +a=6377000 +b=6377000" )
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# Ortograska projekcija
ortho_proj <- "+proj=ortho +lat_0=40 +lon_0=70"
bgtk = st_sfc(bg, tk, crs ="+proj=longlat +a=6377000 +b=6377000")
# Karta koristeći ggplot
ggplot() +
geom_sf(data = world, fill = "lightgray", color = "white") +
geom_sf(data = lines, color = c("blue", "red"), size = 1) +
geom_sf(data = bgtk, size = 3, color = c("black", "green") ) +
labs(title = "Geodeska linija (plava) i Loksodroma (crvena)",
subtitle = "Ortografska projekcija",
caption = "Crni simbol: Beograd, Zeleni simbol: Tokio") +
theme_minimal() +
coord_sf(crs = ortho_proj)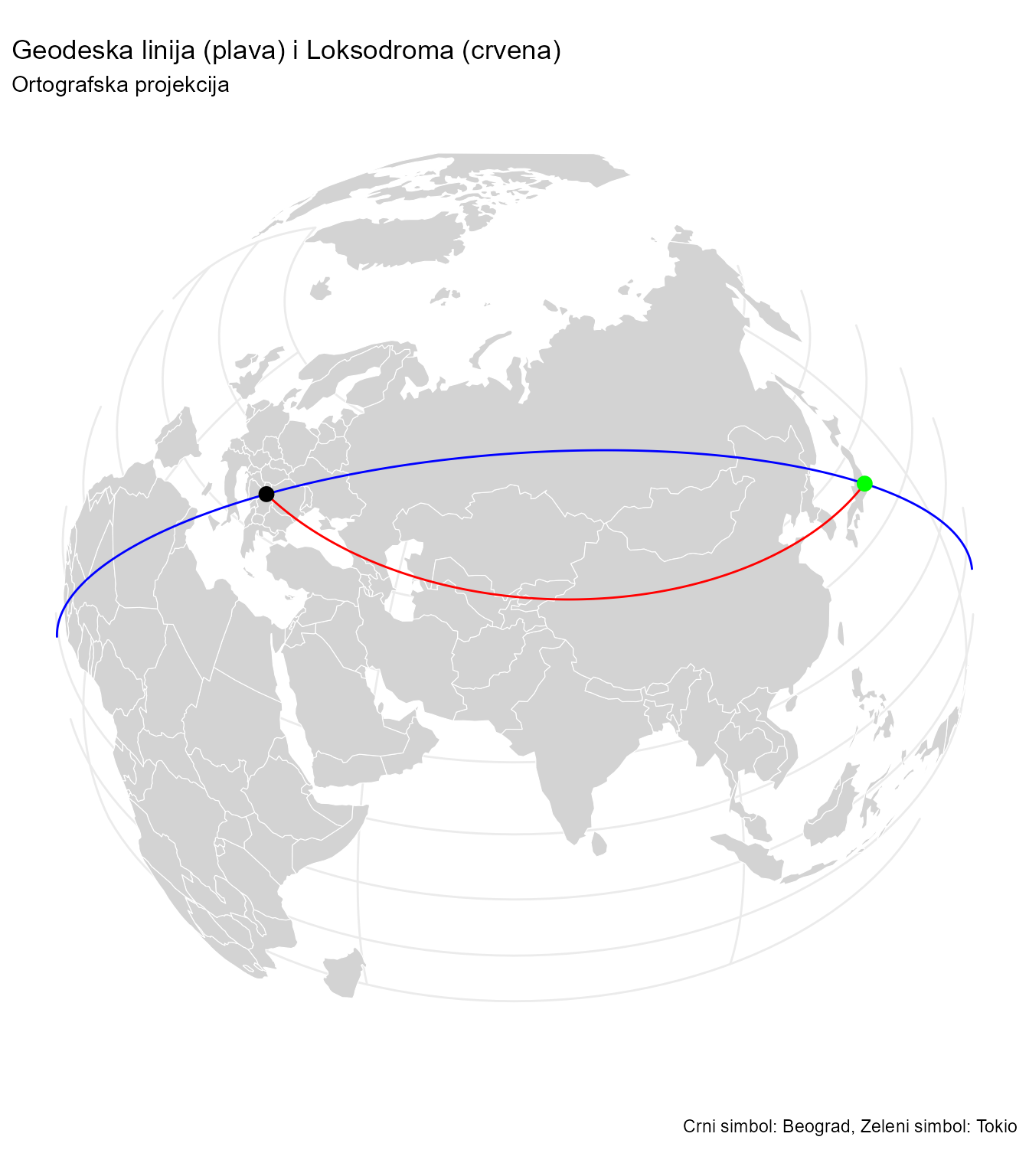
6.4 Kratak osvrt na istorijski značaj perspektivnih projekcija
Najstarija kartografska projekcija (gnomonska ili centralna) pripisuje se Talesu Miletskom (639‒548), a korišćena je za kartu zvezdanog neba. Zatim sledi ortografska projekcija koju je predložio Apolonije iz Perga (262‒190), pa stereografska projekcija koju je obradio Hiparh (već pomenuti grčki naučnik iz 2. v. pre n.e.) i koristio je za izradu svoje geografske karte. Hiparh je, takođe, razradio ortografsku perspektivnu projekciju, kao i prostu konusnu projekciju, i ukazao na metod sastavljanja karata na osnovu astronomskih tačaka (Jovanović (1984)).
6.5 Lambertova azimutna ekvivalentna projekcija
Lambertova azimutna ekvivalentna projekcija nije prava perspektiva, formule se izvode analitičkim putem. Površine se ne deformišu. Formule za direktna računanja kod pravog oblika definisane su izrazima (Jovanović (1984)):
\[ \begin{aligned} & \delta=\lambda \\ & \rho=2 R \sin \left(45^{\circ}-\frac{\varphi}{2}\right) \\ & x=2 R \sin \left(45^{\circ}-\frac{\varphi}{2}\right) \cos \lambda \\ & y=2 R \sin \left(45^{\circ}-\frac{\varphi}{2}\right) \sin \lambda \\ & \mu_z=\cos \left(45^{\circ}-\frac{\varphi}{2}\right) \\ & \mu_a=\sec \left(45^{\circ}-\frac{\varphi}{2}\right) \\ & p=1 \\ & \operatorname{tg}\left(45^{\circ}+\frac{\omega}{4}\right)=\sec \left(45^{\circ}-\frac{\varphi}{2}\right) . \end{aligned} \] Formule za direktna računanja kod kosog oblika definisane su izrazima (Jovanović (1984)):
\[ \begin{aligned} & \delta=a_z \quad, a_z \quad \text{je zenitni azimut} \\ & \rho=2 R \sin \frac{z}{2} \\ & x=2 R \sin \frac{z}{2} \cos a_z \\ & y=2 R \sin \frac{z}{2} \sin a_z \\ & \mu_z=\cos \frac{z}{2} \\ & \mu_a=\sec \frac{z}{2} \\ & p=1 \\ & \operatorname{tg}\left(45^{\circ}+\frac{\omega}{4}\right)=\sec \frac{z}{2} . \end{aligned} \] Gde je: \[ \begin{aligned} & \sin z \cos a_z=\sin \varphi \cos \varphi_0-\sin \varphi_0 \cos \varphi \cos \lambda \\ & \sin z \sin a_z=\sin \lambda \cos \varphi \\ & \cos z=\sin \varphi_o \sin \varphi+\cos \varphi_0 \cos \varphi \cos \lambda \end{aligned} \]
Inverzni zadatak je definisan formulama (Snyder (1987)):
\[ \varphi=\arcsin \left[\cos z \sin \varphi_0+\left(y \sin z \cos \varphi_0 / \rho\right)\right] \] Ako \(\varphi_0 \neq\pm 90^{\circ}\) : \[ \lambda=\lambda_0+\arctan \left[x \sin z /\left(\rho \cos \varphi_0 \cos z-y \sin \varphi_0 \sin z\right)\right] \] Ako je \(\varphi_0=90^{\circ}\) :
\[ \lambda=\lambda_0+\arctan [x /(-y)] \]
Ako je \(\varphi_0=-90^{\circ}\) :
\[ \lambda=\lambda_0+\arctan (x / y) \]
Lambertova azimutna ekvivalentna projekcija koristi se za mnoge panevropske setove podataka, tako na primer Evropski digitalni model terena, Corine Land Cover podaci, statistički panevropski prostorni podaci su u Lambertovoj ekvivalentnoj projekciji zadatom sa sledećim parametrima (EPSG:3035):
+proj=laea +lat_0=52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crsElipse deformacija u Lambertovoj azimutnoj ekvivalentnoj projekciji, Slika 6.12. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 300 km na elipsoidu i odgovarajuće površine u projekciji.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(-180,180, by=60)
f = seq(-90,90,by=15) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +type=crs")
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
sf_use_s2(FALSE) # koristi elispoidna računanja
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u 3035 projekciji
tissot.ort <- st_transform(tissot.sf, 3035)
# površine u projekciji
tissot.ort$a_proj <- st_area(tissot.ort)
# odnos površina u projekciji i na sferi
tissot.ort$p <- tissot.ort$a_proj/tissot.ort$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_laea = st_transform(world, crs = 3035)
ll = st_centroid(tissot.ort)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_laea), graticule = TRUE,
col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.ort),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.ort$p,1)) ,col='red' , cex = 0.8)
6.6 Azimutna ekvidistantna projekcija
Azimutna ekvidistantna projekcija, kao i Lambertova azimutna ekvivalentna, nije perspektivna projekcija. Ima azimutnu karakteristiku da su svi pravci ili azimuti tačni kada se mere od centralne, tangentne tačke. Kao posebna karakteristika, sve udaljenosti su u pravom razmeru kada se mere između ovog centra i bilo koje druge tačke na karti, dakle projekcija je uslovna i spada u grupu ekvidistantnih gde se pojedine dužine ne deformišu.
Grupisane formule za direktna računanja (Jovanović (1984)):
\[ \begin{aligned} & \delta=a_z \quad, a_z \quad \text{je zenitni azimut} \\ & \rho=R z \\ & x=R z \cos a_z \\ & y=R z \sin a_z \\ & \mu_z=1 \\ & \mu_a=\frac{z}{\sin z} \\ & \rho=\frac{z}{\sin z} \\ & \sin \frac{\omega}{2}=\frac{\mu_z-\mu_a}{\mu_z+\mu_a} ;\left(\text { ili }: \frac{\mu_a-\mu_z}{\mu_z+\mu_a}\right) . \end{aligned} \] Gde je:
\[ \begin{aligned} & \sin z \cos a_z=\sin \varphi \cos \varphi_0-\sin \varphi_0 \cos \varphi \cos \lambda \\ & \sin z \sin a_z=\sin \lambda \cos \varphi \\ & \cos z=\sin \varphi_o \sin \varphi+\cos \varphi_0 \cos \varphi \cos \lambda \end{aligned} \]
Inverzne formule (Snyder (1987)):
\[ \phi=\arcsin \left[\cos z \sin \varphi_0+\left(y \sin z \cos \varphi_0 / \rho\right)\right] \] \[ \lambda=\lambda_0+\arctan \left[x \sin z /\left(\rho \cos \varphi_0 \cos z-y \sin \varphi_0 \sin z\right)\right] \] Gde se \(\rho\) i \(z\) računaju po formuli:
\[ \begin{aligned} & \rho=\left(x^2+y^2\right)^{1 / 2} \\ & z=\rho / R \end{aligned} \] Elipse deformacija u Azimutnoj ekvidistantnoj projekciji, Slika 6.13. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 300 km na sferi i odgovarajuće površine u projekciji.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(-180,180, by=60)
f = seq(-90,90,by=15) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +a=6377000 +b=6377000") # sfera R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000, radius=6377000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u aeqd projekciji
aeqd_crs = "+proj=aeqd lat_0=45 lon_0=21 +a=6377000 +b=6377000"
tissot.ort <- st_transform(tissot.sf, aeqd_crs )
# površine u projekciji
tissot.ort$a_proj <- st_area(tissot.ort)
# odnos površina u projekciji i na sferi
tissot.ort$p <- tissot.ort$a_proj/tissot.ort$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_aeqd = st_transform(world, crs = aeqd_crs)
ll = st_centroid(tissot.ort)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_aeqd), graticule = TRUE, col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.ort),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.ort$p,1)) ,col='red' , cex = 0.8)
6.7 Primeri računanja kod Azimutnih projekcija
Primer 1: Transformisati podatke u Lambertovu ekvivalentnu azimutnu projekciju
Koordinate nekih gradova Evrope date su u sledećoj tabeli:
| Lon | Lat | CITY_NAME | CNTRY_NAME |
|---|---|---|---|
| 37.7 | 55.75 | Moscow | Russia |
| -0.178 | 51.48791 | London | UK |
| 30.25 | 59.91666 | Saint Petersburg | Russia |
| 13.32757 | 52.51627 | Berlin | Germany |
| -3.69097 | 40.44222 | Madrid | Spain |
| 12.52 | 41.88 | Rome | Italy |
| 30.50211 | 50.44816 | Kyiv | Ukraine |
| 2.432997 | 48.882 | Paris | France |
| 26.12297 | 44.43048 | Bucharest | Romania |
| 27.57556 | 53.89994 | Minsk | Belarus |
| 10.028 | 53.571 | Hamburg | Germany |
| 21.01188 | 52.24495 | Warsaw | Poland |
| 19.094 | 47.515 | Budapest | Hungary |
| 2.159001 | 41.358 | Barcelona | Spain |
| 16.32098 | 48.20212 | Vienna | Austria |
| 36.20831 | 49.98967 | Kharkiv | Ukraine |
| 9.189999 | 45.473 | Milan | Italy |
| 43.94067 | 56.28967 | Gorkiy | Russia |
| 20.41256 | 44.79968 | Belgrade | Serbia |
| 11.54295 | 48.14097 | Munich | Germany |
Sračunati koordinate u Lambertovoj ekvivalentnoj azimutnoj projekciji, koja je zadata sledećim prametrima: tangentna tačka 52 severne geodetske širine i 0 geodetske dužine , početna koordinata u pravcu istoka je 4321000 m (false easting), početna koordinata u pravcu severa je 3210000 m (false northing), elipsoid je GRS80 zadat je da se poklapa sa datumskim parametrima sa WGS84.
library(sf)
# podaci iz primera su sačuvani na disku kao csv fajl u folderu data
# čitamo podatke iz csv fajla, pokazujemo kolone sa koorsinatama
# definišemo koor. ref. sis. (CRS)
cts = st_read("data/cities.csv",
options=c("X_POSSIBLE_NAMES=Lon","Y_POSSIBLE_NAMES=Lat"),
crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
# options: X_POSSIBLE_NAMES=Lon Y_POSSIBLE_NAMES=Lat
# Reading layer `cities' from data source `C:\mk_knjiga\data\cities.csv' using driver `CSV'
# Simple feature collection with 20 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -3.69 ymin: 40.4 xmax: 43.9 ymax: 59.9
# Geodetic CRS: +proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs
head(cts)
# Simple feature collection with 6 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -3.69 ymin: 40.4 xmax: 37.7 ymax: 59.9
# Geodetic CRS: +proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs
# Lon Lat CITY_NAME CNTRY_NAME geometry
# 1 37.700 55.7 Moscow Russia POINT (37.7 55.7)
# 2 -0.178 51.5 London UK POINT (-0.178 51.5)
# 3 30.250 59.9 Saint Petersburg Russia POINT (30.2 59.9)
# 4 13.328 52.5 Berlin Germany POINT (13.3 52.5)
# 5 -3.691 40.4 Madrid Spain POINT (-3.69 40.4)
# 6 12.520 41.9 Rome Italy POINT (12.5 41.9)
laea_crs = "+proj=laea +lat_0=52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs" # # EPSG:3035, https://epsg.io/3035
cts_laea = st_transform(cts, crs =3035)
head(cts_laea)
# Simple feature collection with 6 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: 3160000 ymin: 2030000 xmax: 6010000 ymax: 4250000
# Projected CRS: ETRS89-extended / LAEA Europe
# Lon Lat CITY_NAME CNTRY_NAME geometry
# 1 37.700 55.7 Moscow Russia POINT (6011447 3959118)
# 2 -0.178 51.5 London UK POINT (3616690 3202236)
# 3 30.250 59.9 Saint Petersburg Russia POINT (5438576 4251819)
# 4 13.328 52.5 Berlin Germany POINT (4546806 3272610)
# 5 -3.691 40.4 Madrid Spain POINT (3160928 2032431)
# 6 12.520 41.9 Rome Italy POINT (4530909 2089820)
# koordinate treba zaokružiti do na cm
options(digits = 12)
round(st_coordinates(cts_laea),2)
# X Y
# [1,] 6011447.26 3959118.28
# [2,] 3616690.41 3202236.36
# [3,] 5438575.87 4251818.98
# [4,] 4546805.96 3272610.38
# [5,] 3160928.34 2032430.65
# [6,] 4530909.19 2089820.04
# [7,] 5755398.99 3240164.26
# [8,] 3766950.27 2891684.58
# [9,] 5596061.41 2507115.90
# [10,] 5463332.46 3561130.19
# [11,] 4322855.05 3384816.29
# [12,] 5069830.22 3294038.22
# [13,] 5004471.50 2753330.08
# [14,] 3663507.73 2062688.76
# [15,] 4790425.77 2807728.25
# [16,] 6154636.72 3319535.62
# [17,] 4257568.07 2484860.66
# [18,] 6333273.46 4177161.69
# [19,] 5143326.66 2467248.75
# [20,] 4435876.29 2782024.24
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import geopandas as gpd
# čitamo podatke iz csv fajla, pokazujemo kolone sa koorsinatama
# definišemo koordinatni referentni sistem (CRS)
cts = gpd.read_file("data/cities.csv" , driver="CSV", X_POSSIBLE_NAMES="Lon", Y_POSSIBLE_NAMES="Lat")
cts.crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs"
print(cts.head())
# Lon Lat CITY_NAME CNTRY_NAME geometry
# 0 37.700001 55.749996 Moscow Russia POINT (37.70000 55.75000)
# 1 -0.178002 51.487911 London UK POINT (-0.17800 51.48791)
# 2 30.249999 59.916663 Saint Petersburg Russia POINT (30.25000 59.91666)
# 3 13.327569 52.516269 Berlin Germany POINT (13.32757 52.51627)
# 4 -3.690972 40.442220 Madrid Spain POINT (-3.69097 40.44222)
# transformacija u LCC
laea_crs = "+proj=laea +lat_0=52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs +type=crs" # # EPSG:3035, https://epsg.io/303
cts_laea = cts.to_crs(3035)
print(cts_laea.head())
# Lon Lat ... CNTRY_NAME geometry
# 0 37.700001 55.749996 ... Russia POINT (6011447.262 3959118.282)
# 1 -0.178002 51.487911 ... UK POINT (3616690.408 3202236.364)
# 2 30.249999 59.916663 ... Russia POINT (5438575.867 4251818.978)
# 3 13.327569 52.516269 ... Germany POINT (4546805.963 3272610.381)
# 4 -3.690972 40.442220 ... Spain POINT (3160928.335 2032430.647)
#
# [5 rows x 5 columns]
# koordinate na cm
cts_laea['X'] = cts_laea['geometry'].x.round(2)
cts_laea['Y'] = cts_laea['geometry'].y.round(2)
# odbacujemo originalnu geometriju
cts_laea = cts_laea.drop(columns='geometry')
print(cts_laea)
# Lon Lat CITY_NAME CNTRY_NAME X Y
# 0 37.700001 55.749996 Moscow Russia 6011447.26 3959118.28
# 1 -0.178002 51.487911 London UK 3616690.41 3202236.36
# 2 30.249999 59.916663 Saint Petersburg Russia 5438575.87 4251818.98
# 3 13.327569 52.516269 Berlin Germany 4546805.96 3272610.38
# 4 -3.690972 40.442220 Madrid Spain 3160928.34 2032430.65
# 5 12.519999 41.879997 Rome Italy 4530909.19 2089820.04
# 6 30.502107 50.448159 Kyiv Ukraine 5755398.99 3240164.26
# 7 2.432997 48.881997 Paris France 3766950.27 2891684.58
# 8 26.122968 44.430480 Bucharest Romania 5596061.41 2507115.90
# 9 27.575559 53.899938 Minsk Belarus 5463332.46 3561130.19
# 10 10.027998 53.570997 Hamburg Germany 4322855.05 3384816.29
# 11 21.011877 52.244946 Warsaw Poland 5069830.22 3294038.22
# 12 19.094004 47.514996 Budapest Hungary 5004471.50 2753330.08
# 13 2.159001 41.357997 Barcelona Spain 3663507.73 2062688.76
# 14 16.320978 48.202119 Vienna Austria 4790425.77 2807728.25
# 15 36.208305 49.989672 Kharkiv Ukraine 6154636.72 3319535.62
# 16 9.189999 45.473004 Milan Italy 4257568.07 2484860.66
# 17 43.940673 56.289672 Gorkiy Russia 6333273.46 4177161.69
# 18 20.412558 44.799678 Belgrade Serbia 5143326.66 2467248.75
# 19 11.542950 48.140973 Munich Germany 4435876.29 2782024.24Primer 2: Koristeći prethodne podatke i granice država u Evropi kreirati kartu u Lambertovoj azimutnoj ekvivalentnoj projekciji
library(sf)
library(spData)
cts = st_read("data/cities.csv",
options=c("X_POSSIBLE_NAMES=Lon","Y_POSSIBLE_NAMES=Lat"),
crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
# options: X_POSSIBLE_NAMES=Lon Y_POSSIBLE_NAMES=Lat
# Reading layer `cities' from data source `C:\mk_knjiga\data\cities.csv' using driver `CSV'
# Simple feature collection with 20 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -3.69 ymin: 40.4 xmax: 43.9 ymax: 59.9
# Geodetic CRS: +proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs
cts_laea = st_transform(cts, crs = 3035)
# koordinate za toponime
ll= st_coordinates(cts_laea)
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# izdvojimo okvirno Evropu
sf_use_s2(FALSE)
eur <- st_crop(world, xmin = -20, xmax = 45,
ymin = 30, ymax = 73)
sf_use_s2(TRUE)
eur_laea = st_transform(eur,
crs = 3035)
# Karta
plot(st_geometry(eur_laea), graticule = TRUE, col= 'gray',
border ='black', axes = TRUE)
plot(st_geometry(cts_laea), pch = 20, add = TRUE, col='darkblue')
text(ll[, 1], ll[, 2], cts_laea$CITY_NAME ,col='darkblue',
cex=0.7, pos = 3, offset = 0.1)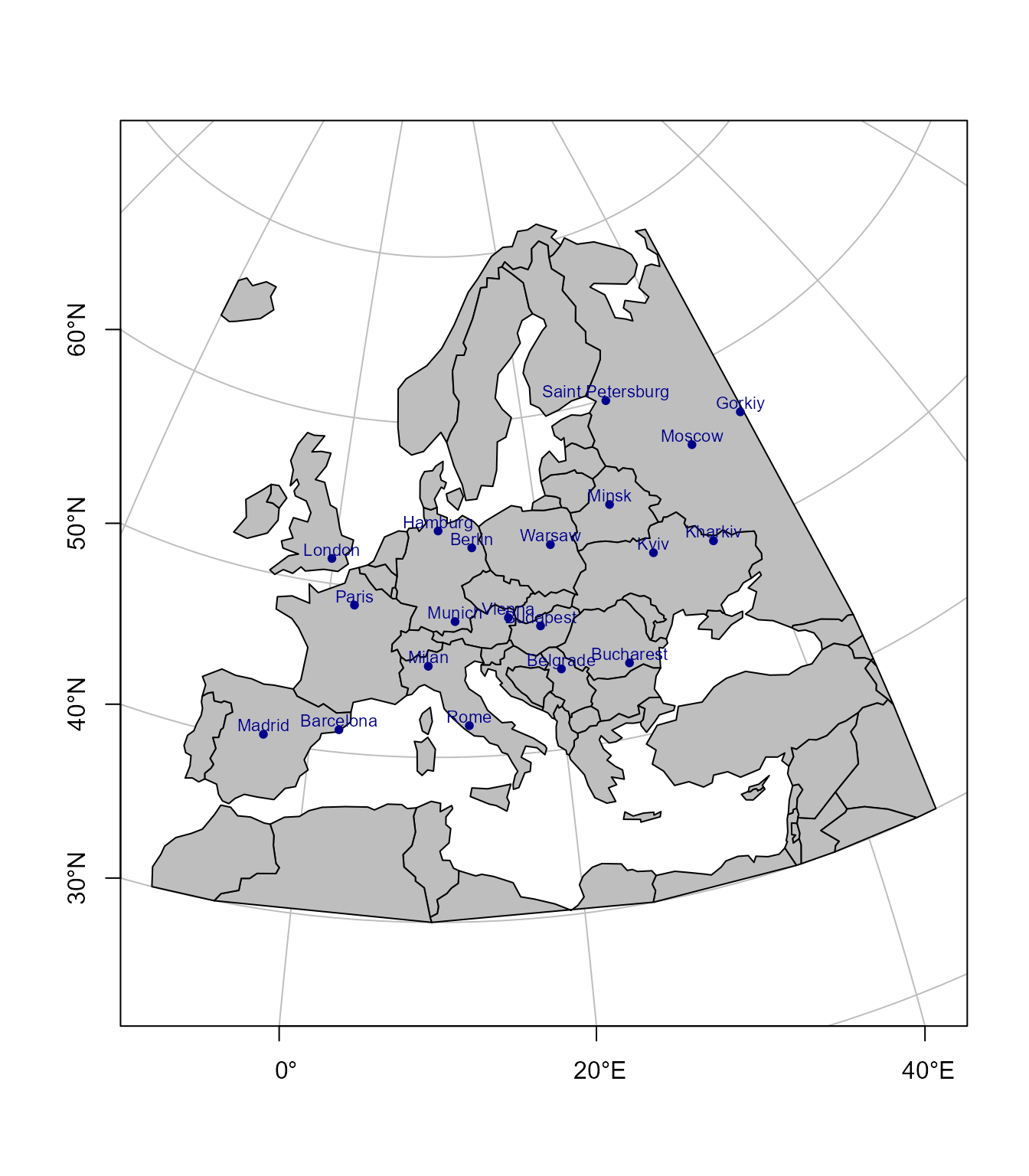
import geopandas as gpd
from shapely.geometry import Point,box
import matplotlib.pyplot as plt
# čitamo podatke iz csv fajla, pokazujemo kolone sa koorsinatama
# definišemo koordinatni referentni sistem (CRS)
cts = gpd.read_file("data/cities.csv" , driver="CSV", X_POSSIBLE_NAMES="Lon", Y_POSSIBLE_NAMES="Lat")
cts.crs = "+proj=longlat +ellps=GRS80 +datum=WGS84"
cts = cts.to_crs(crs=3035)
# Koordinate za toponime
# ll = cts.geometry.apply(lambda geom: (geom.x, geom.y))
cts['X'] = cts['geometry'].x.round(2)
cts['Y'] = cts['geometry'].y.round(2)
# Granice država
# https://github.com/Nowosad/spData/blob/master/inst/shapes/world.gpkg
world = gpd.read_file("data/world.gpkg")
# poligon za clip
polygon = box(-20, 30, 45, 73)
poly_gdf = gpd.GeoDataFrame([1], geometry=[polygon], crs=3035)
# eur = world.cx[-20:45, 30:73]
eur = world.clip(poly_gdf)
# C:\Users\user\AppData\Local\Programs\Python\PYTHON~1\lib\site-packages\geopandas\geodataframe.py:2361: UserWarning: CRS mismatch between the CRS of left geometries and the CRS of right geometries.
# Use `to_crs()` to reproject one of the input geometries to match the CRS of the other.
#
# Left CRS: EPSG:4326
# Right CRS: EPSG:3035
#
# return geopandas.clip(self, mask=mask, keep_geom_type=keep_geom_type)
# Obrnuti zatak iz filam u lcc
eur = eur.to_crs(crs=3035)
# Plot the map
fig, ax = plt.subplots()
eur.boundary.plot(ax=ax, color='gray')
cts.plot(ax=ax, marker='o', color='darkblue')
for x, y, city_name in zip(cts['X'], cts['Y'], cts['CITY_NAME']):
ax.text(x, y, city_name, color='darkblue', fontsize=7, ha='left', va='top')
ax.set_aspect('equal')
ax.set_axis_off()
plt.show()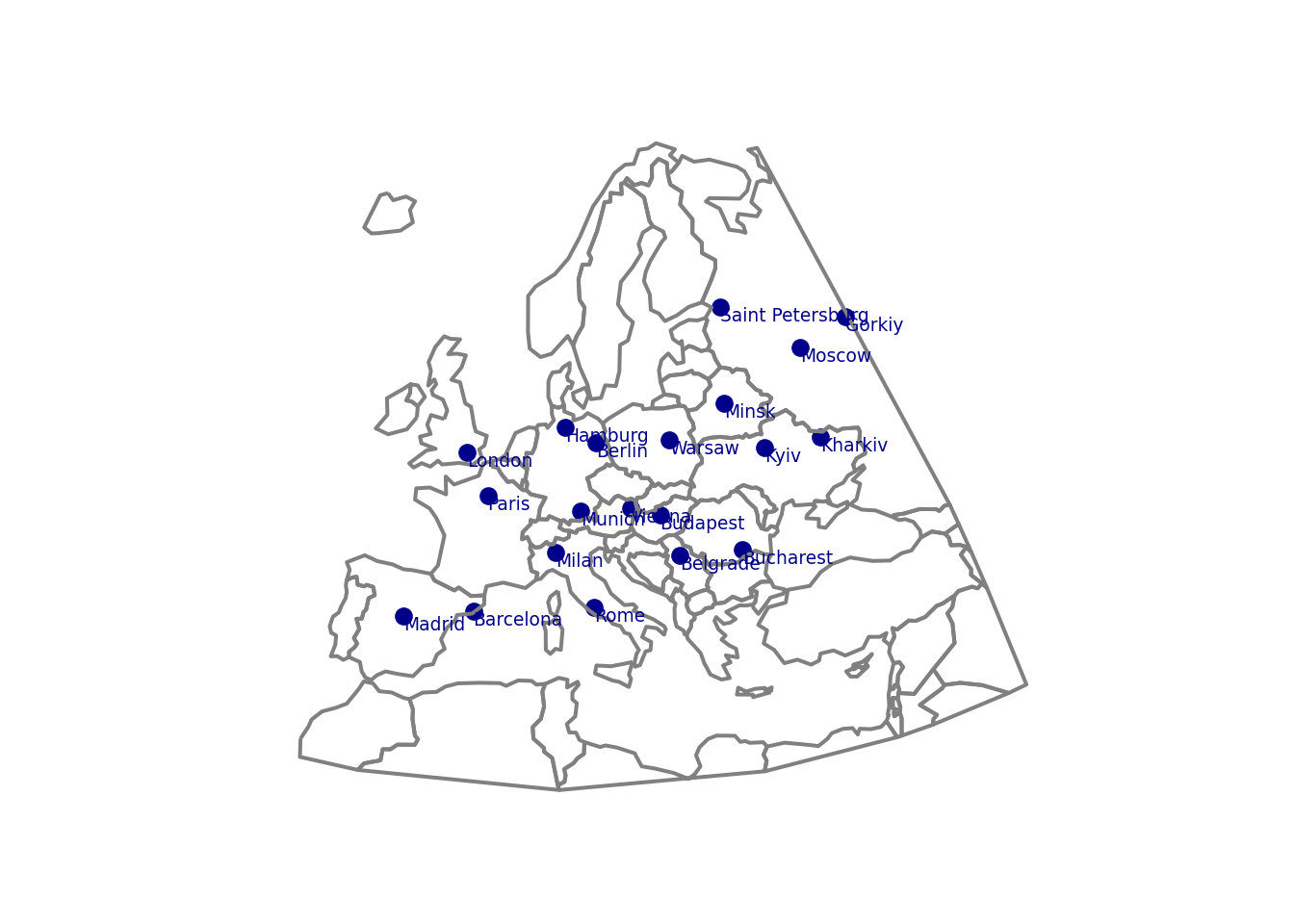
U poglavlju Referentne površi i koordinatni referentni sistemi 2.4.10 sračunali smo da dužina geodetske linije od Beograda (\(\varphi=44.800153\) i \(\lambda=20.455727\)) do Tokija (\(\varphi=35.679207\) i \(\lambda=139.767118\)) iznosi 9184644 m (9185 km) na WGS84. Sračunati dužinu u Azimutnoj ekvidistantnoj projkeciji, gde je centralna tačka Beograd, a preslikavanje sa sfere poluprečnika R=6377 km.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# geometrija bg, tk
bg = st_point( c(20.455727, 44.800153) ) # lon , lat
tk = st_point( c(139.767118, 35.679207) ) # lon , lat
# potom pravimo kolekciju geometrije sfc
pts_sfc = st_sfc(c(bg,tk), crs="+proj=longlat +a=6377000 +b=6377000")
#
eqd_crs = "+proj=aeqd lat_0=44.800153 lon_0=20.455727 +a=6377000 +b=6377000"
# transformacija u az ek dist
pts_sfc_M = st_transform(pts_sfc, crs = eqd_crs)
st_coordinates(pts_sfc_M)
# X Y L1
# [1,] 0.00000 0.00000 1
# [2,] 6566286.91907 6434304.24388 1
# matrica koordinata iz prostornih podataka
EN=st_coordinates(pts_sfc_M)
# računamo dužinu iz koordinata
Dgl = sqrt(diff(EN[,1])^2 +diff(EN[,2])^2)
# dužina u m
round(Dgl)
# [1] 9193280
# dužina u km
round(Dgl/1000)
# [1] 9193
# a dužina na elispoidu WGS84 je 9185 km
import shapely.geometry
import geopandas as gpd
# pravimo GeoDataFrame bg, tk
bg = shapely.geometry.Point( 20.455727, 44.800153) # lon , lat
tk = shapely.geometry.Point( 139.767118, 35.679207) # lon , lat
data = {'geometry': [bg, tk]}
bgtk = gpd.GeoDataFrame(data, crs="+proj=longlat +a=6377000 +b=6377000")
# transformacija u az eq dist
eqd_crs = "+proj=aeqd lat_0=44.800153 lon_0=20.455727 +a=6377000 +b=6377000"
bgtk = bgtk.to_crs(eqd_crs)
print(bgtk)
# geometry
# 0 POINT (0.000 0.000)
# 1 POINT (6566286.919 6434304.244)
# Prikaz koordinata na 6 decimala
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
E = bgtk["geometry"].x
N = bgtk["geometry"].y
# računamo dužinu iz koordinata
Dgl = ((E[1]-E[0])**2 +(N[1]-N[0])**2)**0.5
# dužina u m
print( round(Dgl) )
# 9193280
# dužina u km
print( round(Dgl/1000) )
# 9193
# a dužina na elispoidu WGS84 je 9185 kmPrimer 4: Inverzni zadatak Lambertova konusna konformna projekcija
Sračunati elipsoidne koordinate za tačke T1(5143326.66, 2467248.75) i T2(4257568.07, 2484860.66) koje su u Lambertovoj ekvivalentnoj azimutnoj projekciji, koja je zadata sledećim prametrima: tangentna tačka 52 severne geodetske širine i 0 geodetske dužine , početna koordinata u pravcu istoka je 4321000 m (false easting), početna koordinata u pravcu severa je 3210000 m (false northing), elipsoid je GRS80 zadat je da se poklapa sa datumskim parametrima sa WGS84. Elipsoidne koordinate izraziti i u obliku stepen, minut, sekund.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Za tacke sa koordinatama T1(4797138, 2081947) i T2(4110994, 2386560)
# u LAEA projekciji
# Sračunaj koordinate na GRS80 elipsoidu
tLAEA= st_sfc( st_point(c(5143326.66, 2467248.75)), st_point(c(4257568.07, 2484860.66)),
crs = 3035 )
# inverzni zadatak iz pravouglih u longitudu, latitudu
tLL = st_transform(tLAEA,
crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
ll = st_coordinates(tLL)
# Koordinate treba zaokružiti do na cm ili dm, što je oko 6. decimale
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
round(ll,6)
# X Y
# [1,] 20.412558 44.799678
# [2,] 9.189999 45.473004
# gedetska dužina i širina
# lon lat
lon = ll[,1]
lat = ll[,2]
# funkcija za stepen u stepen minut sekund
deg2dms <- function(deg){
deg_sign = sign(deg)
deg = abs(deg)
DEG = floor(deg)
MIN = floor((deg - DEG) * 60)
SEC = (deg - DEG - MIN/60) * 3600
SEC=round(SEC,2)
dms=paste(deg_sign*DEG,'\u00B0',MIN,"'",SEC,"''",sep='')
return(dms)
}
# gedetska dužina i širina
print(paste("T1 " ,deg2dms(lon[1]), deg2dms(lat[1])) )
# [1] "T1 20°24'45.21'' 44°47'58.84''"
print(paste( "T2 " ,deg2dms(lon[2]), deg2dms(lat[2])) )
# [1] "T2 9°11'24'' 45°28'22.81''"import shapely.geometry
import geopandas as gpd
# pravimo GeoDataFrame koordinate u LCC projekciji
data = {'geometry': [shapely.geometry.Point(5143326.66, 2467248.75), shapely.geometry.Point(4257568.07, 2484860.66)]}
gdf = gpd.GeoDataFrame(data, crs=3035) # LAEA
# transformacija u GRS80
gdf_grs80 = gdf.to_crs("+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
print(gdf_grs80)
# geometry
# 0 POINT (20.41256 44.79968)
# 1 POINT (9.19000 45.47300)
# Prikaz koordinata na 6 decimala
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
lon = gdf_grs80["geometry"].x
lat = gdf_grs80["geometry"].y
# gedetska dužina i širina
print("T1 " ,round(lon[0],6), round(lat[0],6))
# T1 20.412558 44.799678
print("T2 " ,round(lon[1],6), round(lat[1],6))
# T2 9.189999 45.473004
# funkcija za stepen u stepen minut sekund
def deg2dms(deg):
deg_sign = 1 if deg >= 0 else -1
deg = abs(deg)
DEG = int(deg)
MIN = int((deg - DEG) * 60)
SEC = (deg - DEG - MIN / 60) * 3600
SEC = round(SEC, 2)
dms = f"{deg_sign * DEG}\u00B0{MIN}'{SEC}''"
return dms
# gedetska dužina i širina
print(f"T1 {deg2dms(lon[0])} {deg2dms(lat[0])}")
# T1 20°24'45.21'' 44°47'58.84''
print(f"T2 {deg2dms(lon[1])} {deg2dms(lat[1])}")
# T2 9°11'24.0'' 45°28'22.81''