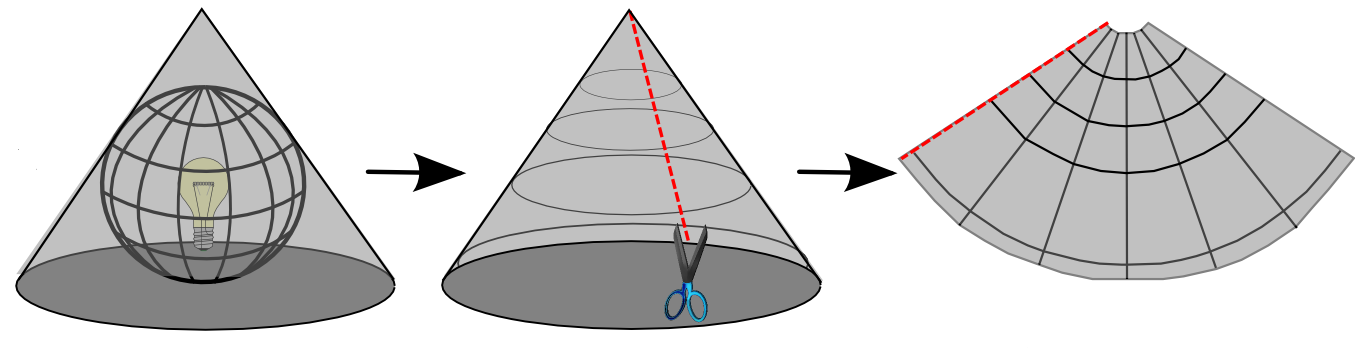
5 Konusne projekcije
Cilindrične projekcije se prvenstveno koriste za karte sveta, globalne karte. Da bi se prikazao region koji se prostire pretežno u pravcu istok-zapad, ako želimo da imamo manje deformacije, više se primenjuju konusne projekcije u odnosu na cilindrične. Naziv „konusne“ potiče od toga što je pomoćna površ pri projiciranju konus koji je kod normalnih konusnih projekcija takav da mu se vrh nalazi na osi rotacije obrtnog elipsoida, a dodiruje elipsoid po tangentnoj ili standardnoj paraleli na kojoj nema deformacija dužina.
U ovom poglavlju predstavićemo različite varijacije konusnih projekcija, naglašavajući njihove ključne karakteristike i primene. Fokusiraćemo se na prave konusne projekcije, proučavajući metode određivanja konstante proporcionalnosti „k“ kod dodirnog konusa. U sledećem delu opisaćemo i razraditi pravu konformnu konusnu projekciju, naglašavajući njen značaj za očuvanje uglova i oblika sa varijantom dodirnog i sekućeg konusa. Na kraju, koristićemo Lambertovu konusnu konformnu projekciju kako bismo pružili praktične primere računanja. Ovaj odeljak će čitaocima omogućiti da prodube svoje razumevanje konusnih projekcija i da znaju kako da ih primenjuju u praksi.
Mreža meridijana i paralela kod konusnih projekcija najočiglednije se predstavlja kao projiciranje površi Zemljine lopte ili elipsoida na plašt konusa, koji se potom razvija na ravan (Slika 5.1). U prošlosti se preslikavanje vršilo postupcima koji se baziraju na primeni linearne perspektive. Razvojem matematike i matematičke kartografije ovo preslikavanje se definiše analitičkim funkcijama preslikavanja uz unapred definisane uslove preslikavanja. Kod pravih konusnih projekcija kartografska mreža je sastavljena od međusobno ortogonalnih linija:
- paralele su lukovi koncentričnih krugova,
- meridijani su prave linije upravne na lukove koji su slika paralela.
To znači da su kod pravih konusnih projekcija meridijani i paralele istovremeno i glavni pravci, jer je mreža meridijana i paralela ortogonalna kao i na originalnoj površi.
Konus može biti tangirajući ili sekući i zauzimati normalan (prav, uspravan), kos ili poprečan (transferzalan) položaj u odnosu na površ Zemljinog elipsoida ili lopte, Slika 4.2. U odnosu na deformacije konusne projekcije mogu biti: konformne, ekvivalentne i uslovne.

Kod pravih konusnih projekcija linije kontakta između površi konusa i elipsoida (lopte) uvek su paralele, i to jedna dodirna ili dve sekuće paralele, Slika 5.3. Duž njih nema deformacije dužina, pa se u literaturi sreću pod nazivom „linije nultih linijskih deformacija“ ili tzv. standardne, odnosno glavne paralele. Ako se ovo ima u vidu, jasno je da će primena tangirajućeg ili sekućeg konusa zavisiti, u prvom redu, od veličine teritorije koja se preslikava.
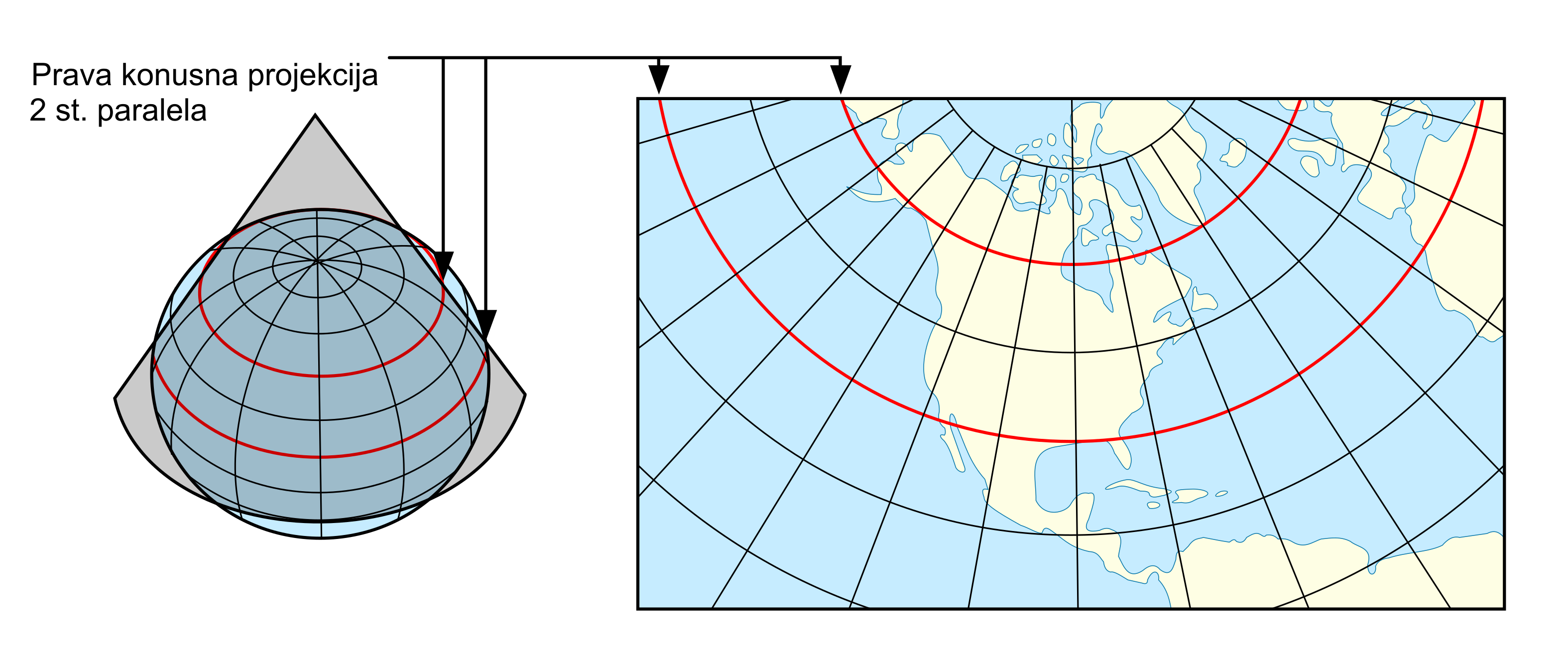
Za područje relativno usko po širini (širina pojasa \(6^o-7^o\)) koristi se tangirajući konus, a standardna (dodirna) paralela bira se po sredini pojasa. Za teritorije sa većim protezanjem po širini, koristi se sekući konus, a standardne (sekuće) paralele postavljaju se tako da se obezbedi ravnomeran raspored deformacija. Ovo se, načelno, postiže ako se standardne paralele postave na 1/6 i 5/6 ukupne dužine odsečka srednjeg meridijana, zahvaćenog preslikavanjem (Jovanović 1984).
5.1 Prave konusne projekcije
Opšte jednačine pravih konusnih projekcija kojima se određuju položaji preslikanih tačaka u polarnom i pravouglom sistemu koordinata u ravni, Slika 5.4.
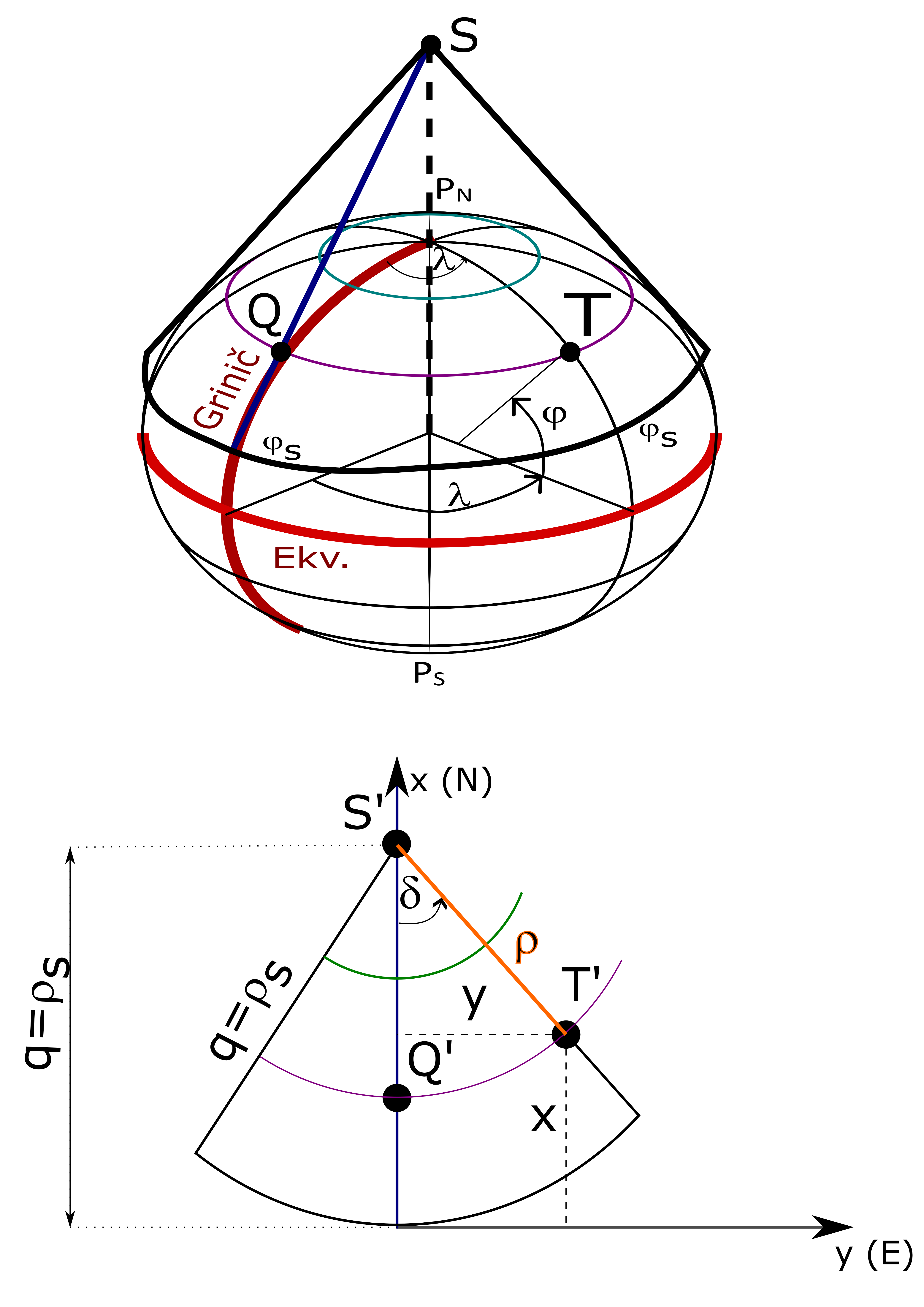
Možemo definisati pravougle koordinate (Slika 5.4):
\[ x=q-\rho \cos \delta=\rho_s-\rho \cos \delta \]
\[ y=\rho \sin \delta \]
Očigledno je da u zavisnosti od položaja temena konusa (odnosno visine konusa) zavisi koliko je ugao \(\delta\) proporcionalan sa uglom \(\lambda\), geodetskom dužinom.
\[ \delta=k \lambda \]
\[ \rho=\rho(\varphi) \]
Konstanta \(q =\rho_s=konstanta\) je obično radijus luka paralele sa najmanjom (najjužnijom) geodetskom širinom (u razmatranom slučaju najjužnije paralele), \(\rho\) je radijus ostalih paralela u projekciji i 0<k<1.
Postupak izvođenja je jednostavniji u odnosu na Jovanović (1984) i polazi direktno od primene opšteg slučaja kartografskog preslikavanja Opšte jednačine kartografskih projekcija 3.3, kao što je razmatrana i Merkatorova projekcija. Kad znamo opšte funkcije preslikavanja možemo odrediti Gausove fundamentalne veličine:
\[ E=\left(\frac{\partial(x(\varphi, \lambda))}{\partial \varphi}\right)^2+\left(\frac{\partial(y(\varphi, \lambda))}{\partial \varphi}\right)^2 \]
\[ \mathrm{F}=\frac{\partial(x(\varphi, \lambda))}{\partial \varphi} \frac{\partial(x(\varphi, \lambda))}{\partial \lambda}+\frac{\partial(y(\varphi, \lambda))}{\partial \varphi} \frac{\partial(y(\varphi, \lambda))}{\partial \lambda} \]
\[ G=\left(\frac{\partial(x(\varphi, \lambda))}{\partial \lambda}\right)^2+\left(\frac{\partial(y(\varphi, \lambda))}{\partial \lambda}\right)^2 \]
Za to su nam neophodni parcijalni izvodi:
\[ x_{\varphi}=q_{\varphi}-\rho_{\varphi} \cos \delta+\rho \sin \delta \delta_{\varphi} \]
\[ y_{\varphi}=\rho_{\varphi} \sin \delta+\rho \cos \delta \delta_{\varphi} \]
\[ x_\lambda=\rho \sin \delta \delta_\lambda \]
\[ y_\lambda=\rho \cos \delta \delta_\lambda \]
Pošto je očigledno da \(\delta\) zavisi samo od geodetske dužine, a \(\rho\) od geodetske širine, dok je \(q\) konstanta, imamo da važi:
\[ \begin{aligned} & \frac{\partial \delta}{\partial \varphi}=0 \\ & \frac{\partial \delta}{\partial \lambda}=k \end{aligned} \]
Tako da su parcijalni izvodi:
\[ x_{\varphi}=-\rho_{\varphi} \cos \delta \]
\[ y_{\varphi}=\rho_{\varphi} \sin \delta \]
\[ x_\lambda=\rho \sin \delta \delta_\lambda = k\rho \sin \delta \]
\[ y_\lambda=\rho \cos \delta \delta_\lambda = k\rho \cos \delta \]
Dalje imamo da je Gausova fundamentalna veličine \(E\):
\[ E=x_{\varphi}^2+y_{\varphi}^2=\rho_{\varphi}^2\left(\sin^2 \delta+\cos^2 \delta\right)=\rho_{\varphi}^2 \]
Veličina \(F\) je:
\[ F=x_{\varphi} x_\lambda+y_{\varphi} y_\lambda=-k \rho_{\varphi} \rho \sin \delta \cos \delta+k \rho_{\varphi} \rho \sin \delta \cos \delta=0 \] Kod ortogonalne mreže u projekciji unapred smo znali da je \(F=0\).
Končno \(G\) je:
\[ G=x_\lambda^2+y_\lambda^2=k^2 \cdot \rho^2 \]
Kad znamo Gausove fundamentalne veličine jednostavno je odrediti linearnu razmeru u pravcu meridijana \(m=\frac{\sqrt{E}}{M}\):
\[ m=\frac{\sqrt{E}}{M}=\frac{-\rho_\varphi }{M} \]
Odredimo potom razmeru u pravcu paralele (\(n=\frac{\sqrt{G}}{N\cos\varphi}=\frac{\sqrt{G}}{r}\)):
\[ n=\frac{\sqrt{G}}{N cos \varphi}=\frac{k\rho}{r} \]
Ugao između meridijana i paralela u projekciji je \(\theta=90^o\), pa zato važi da je \(p=mn\sin(\theta)=mn\):
\[ p=mn\sin(\theta)=mn= -\frac{k \rho \rho_{\varphi}}{M r} \]
Grupisane formule za opšte formule za prave konusne projekcije:
\[ \delta=k \lambda \quad, \quad (0<𝑘<1) \]
\[ \rho=\rho(\varphi) \]
\[ x=q-\rho \cos \delta=q-\rho \cos \delta \]
\[ q=\rho_s=\text { konst } \]
\[ y=\rho \sin \delta \]
\[ m = \frac{- \rho_\varphi}{M} \]
\[ n=\frac{k \rho}{r}=\frac{k \rho}{N \cos \varphi} \]
\[ p=mn\sin(\theta)=mn= -\frac{k \rho \rho_{\varphi}}{M r} \]
\[ \sin \frac{\omega}{2}=\frac{m-n}{m+n} \]
\[ \tan\left(45^{\circ}+\frac{\omega}{4}\right)=\sqrt{\frac{m}{n}} \]
Određivanje konstante proporcionalnosti k kod prave konusne projekcije dodirni konus
Možemo zaključiti (Slika 9.1) da razmak meridijana u projekciji je u polarnim koordinatama označen sa \(\delta\), dok na sferi zavisi od gedetske širine \(\lambda\), odnos ove dve veličine možemo definisati koristeći proporciju na sledeći način:

\[ \frac{\delta}{\lambda}=\frac{\sigma}{2 \pi}=\text { konstanta }=\mathrm{k} \] Do ugla \(\sigma\) možemo doći na slećedi način: Tangirajući krug ima dužinu obima (\(2R\pi\cos\varphi_0\)) , on očuvava dužinu i na slici jer je to dodirna paralela na kojoj nema deformacija. Uočimo M’O’N’, to je deo obima kruga čiji je radijus \(R\cot\varphi_0\). Prema tome, možemo pisati sledeću jednačinu na osnovu definicije ugla u radijanima da je to odnos dužine luka i poluprečnika:
\[ \sigma=\frac{l u k}{R \_p a r a l e l e_{-} z a_{-} \varphi_0}=\frac{2 \pi R \cos \varphi_0}{R \operatorname{ctg} \varphi_0} \] Tako da možemo odrediti i konstantu \(k\):
\[ k=\frac{\sigma}{2 \pi}=\frac{2 \pi R \cos \varphi_0}{2 \pi R \operatorname{ctg} \varphi_0}=\sin \varphi_0 \]
Analogno kao u prethodnom primeru konstantu projekcije možemo odrediti i kod dodirnog konusa kad se koordinate preslikavaju sa elipsoida, Slika 5.6:
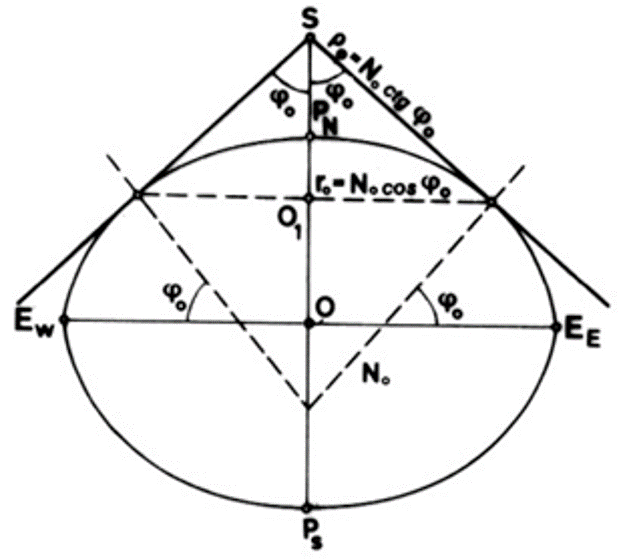
\[ k=\frac{\sigma}{2 \pi}=\frac{2 \pi N_0 \cos \varphi_0}{2 \pi N_0 \operatorname{ctg} \varphi_0}=\sin \varphi_0 \]
5.2 Prava konformna konusna projekcija
Razvijeni oblik funkcije \(\rho = \rho(\varphi)\) tražićemo polazeći od opšteg uslova konformnog preslikavanja, da lokalno nema deformacije uglova, odnosno da je linearna razmera u okolini neke tačke u svim pravcima ista: \(m=n=a=b=c\).
Imamo da je razmera u pravcu meridijana:
\[ m=-\frac{1}{M} \frac{d \rho}{d \varphi} \]
i u pravcu paralele:
\[ n=\frac{k \rho}{r}=\frac{k \rho}{r}=\frac{k \rho}{N \cos \varphi} \]
Ako postavimo uslov da je \(m=n\) imamo:
\[ -\frac{1}{M} \frac{d \rho}{d \varphi}=\frac{k \rho}{r} \] Dalje ako razdvojimo promenljive sa leve i desne strane imamo:
\[ \frac{d \rho}{\rho}=-k \frac{M d \varphi}{r} \]
Ako integralimo izraz, dobijamo:
\[ \ln \rho-\ln K=-k \int \frac{M d \varphi}{r} \] Možemo uočiti da je desna strana integrala rešena u prethodnom poglavlju i predstavlja izometrijsku:
\[ \int \frac{M d \varphi}{r}=\int \frac{M d \varphi}{N \cos \varphi}=\ln U +C \] Gde je:
\[ U=\frac{\tan\left(45^{\circ}+\frac{\varphi}{2}\right)}{\tan^{e}\left(45^{\circ}+\frac{\psi}{2}\right)} \]
\[ e \sin \varphi=\sin \psi \]
\[ e^2=\left(a^2-b^2\right) / a^2 \] Tako da sledi:
\[ \ln \rho-\ln C=-k \ln U \]
\[ \rho=\frac{C}{U^k} \] \(C\) je konstanta integracije, k konstanta projekcije (proporcionalnost).
Tako da ako \(\rho\) zamenimo u formulama za prave konusne konformne projekcije dobićemo:
\[ \delta=k \lambda \]
\[ \rho=\frac{C}{U^k} \]
\[ x=q-\rho \cos \delta \]
\[ y=\rho \sin \delta \]
\[ m=n=k \frac{\rho}{r}=\frac{k}{r} \frac{C}{U^k} \]
\[ p=m n=m^2=n^2=\left(\frac{k}{r} \frac{C}{U^k}\right)^2 \]
\[ \omega=0 \]
Pri čemu su: \(k\) ‒ konstanta projekcije (faktor proporcionalnosti), \(C\) ‒ konstanta integracije.
\[ U=\frac{\operatorname{tg}\left(45^{\circ}+\frac{\varphi}{2}\right)}{\operatorname{tg}^{\mathrm{e}}\left(45^{\circ}+\frac{\psi}{2}\right)} \]
\[ e \sin \varphi=\sin \psi \quad \quad \quad \Rightarrow \quad \quad \quad \psi = arcsin(e \sin \varphi) \]
\[ e^2=\left(a^2-b^2\right) / a^2 \]
Određivanje konstanti kod dodirnog konusa
Konstante \(k\) i \(C\) određuju se uz uslov da je razmer (\(n_0\)) na paraleli zadate širine (\(\varphi_0\)) jednak jedinici i istovremeno najmanji. Polazeći od drugog dela uslova \(n_0 =1\), najpre se određuje konstanta proporcionalnosti \(k=\sin \varphi_0\) (Sekcija 5.1.1), pa zatim konstanta integracije \(C\).
\[ \frac{k}{r} \frac{C}{U^k}=1 \]
\[ \frac{\sin \varphi_0 C}{N_0 \cos \varphi_0 U_0 \sin \varphi_0}=1 \]
\[ C=N_0 \operatorname{ctg} \varphi_0 U_0 \sin \varphi_0 \]
Jasno se vidi iz formula za računanje linearne razmere i razmera površina da se deformacije dužina i površina kod Prave konusne konformne projekcije znatno uvećavaju kad se udaljavamo od standardne paralele, Slika 5.7. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 100 km na elipsoidu i odgovarajuće površine u projekciji.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(-20,45, by=10)
f = seq(30,70,by=5)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = 4326) # WGS84 koordinatni ref. sis.
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 100 km
tissot.sf = st_buffer(tissot.pt, dist = 100000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na elipsoidu
sf_use_s2(FALSE)
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u PKK projekciji
tissot.lcc <- st_transform(tissot.sf,
"+proj=lcc +lat_1=45 +lat_0=45 +lon_0=0 +k_0=1 +ellps=WGS84")
# površine u projekciji
tissot.lcc$a_proj <- st_area(tissot.lcc)
# odnos površina u projekciji i na elipsoidu
tissot.lcc$p <- tissot.lcc$a_proj/tissot.lcc$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# izdvojimo okvirno Evropu
eur <- st_crop(world, xmin = -20, xmax = 45,
ymin = 30, ymax = 73)
sf_use_s2(TRUE)
eur_lcc = st_transform(eur,
crs = "+proj=lcc +lat_1=45 +lat_0=45 +lon_0=0 +k_0=1 +ellps=WGS84")
ll = st_centroid(tissot.lcc)
ll = st_coordinates(ll)
# standardna paralela na 45 stepenu
pts1 = cbind( seq(-20,70,length.out = 100) , rep(45,100) )
ls1 = st_linestring(pts1)
stp = st_sfc(ls1, crs ="+proj=longlat +ellps=GRS80 +datum=WGS84" )
stp = st_transform(stp,
"+proj=lcc +lat_1=45 +lat_0=45 +lon_0=0 +k_0=1 +ellps=WGS84")
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(eur_lcc), graticule = TRUE, col= 'gray', border ='black', axes = TRUE)
plot(stp, col ='blue', add = TRUE) # dodirna paralela
plot(st_geometry(tissot.lcc),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.lcc$p,2)) ,col='red' , cex = 0.8)
Određivanje konstanti kod sekućeg konusa pri konformnom preslikavanju, Lambertova projekcija
Konstante preslikavanja određuju se uz uslov da razmeri \(n_1\) i \(n_2\) na dve standardne paralele zadatih širina (\(\varphi_1\) i \(\varphi_2\)) budu jednaki jedinici (\(n_1 =n_2 =1\)).
\[ \frac{k C}{N_1 \cos \varphi_1 U_1{ }^k}=\frac{k C}{N_1 \cos \varphi_2 U_2{ }^k}=1 \]
\[ N_1 \cos \varphi_1 U_1^k=r_1 U_1^k \]
\[ r_1 U_1^k=r_2 U_2^k \]
\[ \mathrm{k}=\frac{\ln r_1-\ln r_2}{\ln U_2-\ln U_1} \]
\[ \mathrm{C}=\frac{r_1 U_1{ }^k}{k}=\frac{r_2 U_2{ }^k}{k} \]
Kod Lambertove projekcije udaljavanjem od standardnih paralela deformacije dužina i površina rastu, Slika 5.8. Razmeri površina su sračunati kao recipročni odnosi površina kružnica poluprečnika 100 km na elipsoidu i odgovarajuće površine u projekciji. Kod pravih cilindričnih projekcija linije koje spajaju tačke istih deformacija, izokole se poklapaju sa paralelama.
library(sf)
sf_use_s2(TRUE) # koristi sferna računanja
library(spData)
# Koordinate za elipse deformacija
l = seq(-20,45, by=10)
f = seq(30,70,by=5)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = 4326) # WGS84 koordinatni ref. sis.
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 100 km
tissot.sf = st_buffer(tissot.pt, dist = 100000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na elipsoidu
sf_use_s2(FALSE)
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u LCC projekciji
lcc_crs = "+proj=lcc +lat_1=35 +lat_2=65 +ellps=GRS80 +units=m"
tissot.lcc <- st_transform(tissot.sf,
lcc_crs)
# površine u projekciji
tissot.lcc$a_proj <- st_area(tissot.lcc)
# odnos površina u projekciji i na elipsoidu
tissot.lcc$p <- tissot.lcc$a_proj/tissot.lcc$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# izdvojimo okvirno Evropu
eur <- st_crop(world, xmin = -20, xmax = 45,
ymin = 30, ymax = 73)
sf_use_s2(TRUE)
eur_lcc = st_transform(eur,
crs = lcc_crs)
ll = st_centroid(tissot.lcc)
ll = st_coordinates(ll)
# standardne paralele na 35 i 65 stepeni
pts1 = cbind( seq(-20,70,length.out = 100) , rep(35,100) )
pts2 = cbind(seq(-20,70,length.out = 100) , rep(65,100) )
ls1 = st_linestring(pts1)
ls2 = st_linestring(pts2)
stp = st_sfc(ls1,ls2, crs ="+proj=longlat +ellps=GRS80 +datum=WGS84" )
stp = st_transform(stp,
lcc_crs)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(eur_lcc), graticule = TRUE, col= 'gray', border ='black', axes = TRUE)
plot(stp, col ='blue', add = TRUE) # dodirna paralela
plot(st_geometry(tissot.lcc),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.lcc$p,2)) ,col='red' , cex = 0.8)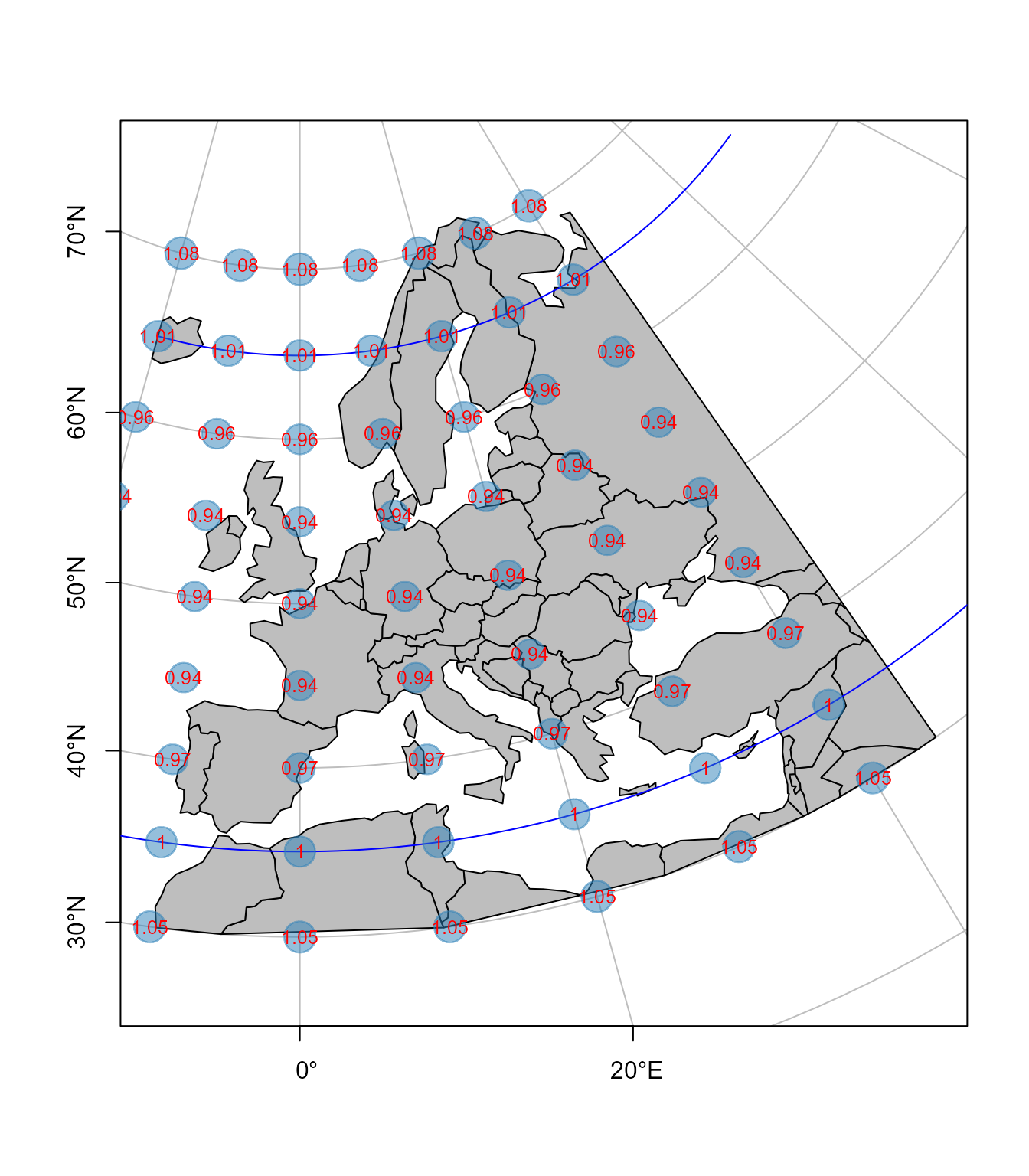
Inverzni zadatak kod Lambertove konusne konformne projekcije
Rešenje za inverzni zadatak dato je sledećim formulama za Lambertovu konusnu konformnu projekciju sa dve standardne paralele (\(\varphi_1\) i \(\varphi_2\)) (Snyder 1987):
\[ \begin{aligned} & \rho= \pm\left[x^2+\left(q-y\right)^2\right]^{1 / 2}, \text { znak od } k, \\ & \delta=\arctan \left[x /\left(q-y\right)\right] \\ & \lambda=\delta / k\\ \end{aligned} \] Ako imamo slučaj da koordinatni početak na elipsoidu nije presek Griniča i najjužnije paralele nego npr. srednji meridijan područja zadat koordinatom \(\lambda_0\) onda geodetska dužina ima oblik:
\[ \lambda=\delta/k+\lambda_0 \]
Kad se rešenje za geodetsku širinu razvije u Tajlorov red, formula je sledeća:
\[ \begin{gathered} \varphi=\chi+\left(e^2 / 2+5 e^4 / 24+e^6 / 12+13 e^8 / 360+\ldots\right) \sin 2 \chi \\ +\left(7 e^4 / 48+29 e^6 / 240+811 e^8 / 11520+\ldots\right) \\ \sin 4 \chi+\left(7 e^6 / 120+81 e^8 / 1120+\ldots\right) \sin 6 \chi \\ +\left(4279 e^8 / 161280+\ldots\right) \sin 8 \chi+\ldots \end{gathered} \]
gde je
\[ \chi=\pi / 2-2 \arctan t \] A \(t\) se računa po formuli:
\[ t=(\rho / a F)^{1 / k} \] gde je \(F\):
\[ F=(\cos \varphi_1 /\left(1-e^2 \sin ^2 \varphi_1\right)^{1 / 2}) /\left(k U_1^k\right) \]
Značaj i primena konusnih projekcija
Deo koji se odnosi na istorijski značaj prave konusne konformne projekcije baziran na knjizi Matematička kartografija, Jovanović (1984).
Ptolemej (100‒170, 2. vek) je pri izradi svojih karata prihvatio Hiparhova uputstva o tome da se tačne geografske karte mogu izrađivati u kartografskim projekcijama uz korišćenje posebnih oslonih tačaka, zadatih geografskom širinom i dužinom. Ipak, ondašnje poznavanje do tada otkrivenog sveta i Zemlje kao planete bilo je dosta oskudno. Verovatno da je među navedenim pozicijama mesta, tek kojih desetak određeno instrumentalnim putem. Karakteristično je da Ptolemej nije poznavao tačne podatke o veličini Zemlje, pa je u izradi karata polazio od toga da je njen obim 18.000 milja, premda su već u to vreme postojala znatno tačnija određivanja, prema Eratostenu. To je razlog što na Ptolemejevim kartama ima velikih netačnosti ‒ njegov se Mediteran prostire na preko 600 dužina, premda je to prostiranje oko \(40^o\) itd. Ova pogrešna predstava o veličini Zemlje, odnosno ubeđenje da je „svet mali“, podstaklo je Kolumba i Magelana da krenu prema Aziji u pravcu zapada.
Najveće zasluge za analitičku razradu konusnih projekcija, specijalno konformnih, pripadaju nemačkom fizičaru, matematičaru i astronomu Lambertu (Johan Heinrich Lambert), odnosno Gausu. Gotovo se sa sigurnošću može tvrditi da početak nove epohe u nauci o kartografskim projekcijama datira sa pojavom Lambertovih radova. Lambert se bavio razmatranjem problema prikazivanja sfere na ravan i razjasnio izvesne opšte uslove koje ovo prikazivanje mora da ispuni, od kojih su najznačajniji očuvanje uglova i konformnost, odnosno jednakost površina (ekvivalentnost). Premda Lambertove dve metode preslikavanja nije razvio do kraja, bio je prvi koji je jasno definisao ideje u odnosu na njih. Prva od njih (konformnost) imala je ogroman značaj za čistu matematiku i prirodne nauke, a obe veliki značaj za kartografiju. Lambert je teoriju konformnih konusnih projekcija razradio još 1772. godine. Rešavajući zadatak preslikavanja jedne površi na drugu pod uslovima očuvanja sličnosti beskonačno malih figura, Gaus je nanovo izveo osobine ove projekcije, publikujući svoje radove 1825. godine.
Lambertova konformna konusna projekcija svoju primenu nalazi u različitim sistemima kartiranja, kao što su aeronautičke karte, specifični delovi koordinatnog sistema državnog, nacionalnog i regionalog nivoa. Evropska agencija za životne sredine u okviru INSPIRE direktive za koordinatne sisteme preporučuju korišćenje ove projekcije (takođe nazvane ETRS89-LCC) za konformno panevropsko kartiranje u razmerama manjim ili jednakim 1:500.000 (Annoni 2003). Lambertova konusna konformna projekcija se koristi i za meteorološke karte Evrope, Slika 5.10, karta pokrivenosti oblacima za 26.7.2023.

5.3 Primeri, Lambertova konusna konformna
Primer 1: Transformisati podatke u Lambertovu konusnu konformnu projekciju
Koordinate nekih gradova Evrope date su u sledećoj tabeli:
| Lon | Lat | CITY_NAME | CNTRY_NAME |
|---|---|---|---|
| 37.7 | 55.75 | Moscow | Russia |
| -0.178 | 51.48791 | London | UK |
| 30.25 | 59.91666 | Saint Petersburg | Russia |
| 13.32757 | 52.51627 | Berlin | Germany |
| -3.69097 | 40.44222 | Madrid | Spain |
| 12.52 | 41.88 | Rome | Italy |
| 30.50211 | 50.44816 | Kyiv | Ukraine |
| 2.432997 | 48.882 | Paris | France |
| 26.12297 | 44.43048 | Bucharest | Romania |
| 27.57556 | 53.89994 | Minsk | Belarus |
| 10.028 | 53.571 | Hamburg | Germany |
| 21.01188 | 52.24495 | Warsaw | Poland |
| 19.094 | 47.515 | Budapest | Hungary |
| 2.159001 | 41.358 | Barcelona | Spain |
| 16.32098 | 48.20212 | Vienna | Austria |
| 36.20831 | 49.98967 | Kharkiv | Ukraine |
| 9.189999 | 45.473 | Milan | Italy |
| 43.94067 | 56.28967 | Gorkiy | Russia |
| 20.41256 | 44.79968 | Belgrade | Serbia |
| 11.54295 | 48.14097 | Munich | Germany |
Sračunati koordinate u Lambertovoj konusnoj konformnoj projekciji, Slika 5.11, koja je zadata sledećim prametrima: sekuće paralele 35 i 65 severne geodetske širine, početna koordinata u pravcu istoka je 4000000 m (false easting), početna koordinata u pravcu severa je 2800000 m (false northing), elipsoid GRS80 zadat je da se poklapa sa datumskim parametrima sa WGS84.

library(sf)
# podaci iz primera su sačuvani na disku kao csv fajl u folderu data
# čitamo podatke iz csv fajla, pokazujemo kolone sa koorsinatama
# definišemo koor. ref. sis. (CRS)
cts = st_read("data/cities.csv",
options=c("X_POSSIBLE_NAMES=Lon","Y_POSSIBLE_NAMES=Lat"),
crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
# options: X_POSSIBLE_NAMES=Lon Y_POSSIBLE_NAMES=Lat
# Reading layer `cities' from data source `C:\mk_knjiga\data\cities.csv' using driver `CSV'
# Simple feature collection with 20 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -3.69 ymin: 40.4 xmax: 43.9 ymax: 59.9
# Geodetic CRS: +proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs
head(cts)
# Simple feature collection with 6 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -3.69 ymin: 40.4 xmax: 37.7 ymax: 59.9
# Geodetic CRS: +proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs
# Lon Lat CITY_NAME CNTRY_NAME geometry
# 1 37.700 55.7 Moscow Russia POINT (37.7 55.7)
# 2 -0.178 51.5 London UK POINT (-0.178 51.5)
# 3 30.250 59.9 Saint Petersburg Russia POINT (30.2 59.9)
# 4 13.328 52.5 Berlin Germany POINT (13.3 52.5)
# 5 -3.691 40.4 Madrid Spain POINT (-3.69 40.4)
# 6 12.520 41.9 Rome Italy POINT (12.5 41.9)
cts_lcc = st_transform(cts,
crs = "+proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +units=m") # EPSG:3034, https://epsg.io/3034
head(cts_lcc)
# Simple feature collection with 6 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: 2870000 ymin: 1660000 xmax: 5650000 ymax: 3810000
# Projected CRS: +proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +units=m
# Lon Lat CITY_NAME CNTRY_NAME geometry
# 1 37.700 55.7 Moscow Russia POINT (5646821 3516023)
# 2 -0.178 51.5 London UK POINT (3319463 2791918)
# 3 30.250 59.9 Saint Petersburg Russia POINT (5094938 3806439)
# 4 13.328 52.5 Berlin Germany POINT (4218148 2860402)
# 5 -3.691 40.4 Madrid Spain POINT (2867442 1658821)
# 6 12.520 41.9 Rome Italy POINT (4204290 1713357)
# koordinate treba zaokružiti do na cm
round(st_coordinates(cts_lcc),2)
# X Y
# [1,] 5646821 3516023
# [2,] 3319463 2791918
# [3,] 5094938 3806439
# [4,] 4218148 2860402
# [5,] 2867442 1658821
# [6,] 4204290 1713357
# [7,] 5388204 2827107
# [8,] 3464710 2492468
# [9,] 5237217 2121363
# [10,] 5106699 3136555
# [11,] 4001793 2968918
# [12,] 4723817 2880358
# [13,] 4660847 2358819
# [14,] 3359416 1687221
# [15,] 4453625 2411387
# [16,] 5777200 2902542
# [17,] 3938581 2098630
# [18,] 5968175 3722088
# [19,] 4797138 2081948
# [20,] 4110994 2386560
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import geopandas as gpd
# čitamo podatke iz csv fajla, pokazujemo kolone sa koorsinatama
# definišemo koordinatni referentni sistem (CRS)
cts = gpd.read_file("data/cities.csv" , driver="CSV", X_POSSIBLE_NAMES="Lon", Y_POSSIBLE_NAMES="Lat")
cts.crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs"
print(cts.head())
# Lon Lat CITY_NAME CNTRY_NAME geometry
# 0 37.700001 55.749996 Moscow Russia POINT (37.70000 55.75000)
# 1 -0.178002 51.487911 London UK POINT (-0.17800 51.48791)
# 2 30.249999 59.916663 Saint Petersburg Russia POINT (30.25000 59.91666)
# 3 13.327569 52.516269 Berlin Germany POINT (13.32757 52.51627)
# 4 -3.690972 40.442220 Madrid Spain POINT (-3.69097 40.44222)
# transformacija u LCC
lcc_crs = "+proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +units=m"
cts_lcc = cts.to_crs(lcc_crs)
print(cts_lcc.head())
# Lon Lat ... CNTRY_NAME geometry
# 0 37.700001 55.749996 ... Russia POINT (5646821.068 3516023.122)
# 1 -0.178002 51.487911 ... UK POINT (3319463.456 2791917.631)
# 2 30.249999 59.916663 ... Russia POINT (5094937.759 3806439.070)
# 3 13.327569 52.516269 ... Germany POINT (4218147.516 2860401.501)
# 4 -3.690972 40.442220 ... Spain POINT (2867441.738 1658821.401)
#
# [5 rows x 5 columns]
# koordinate na cm
cts_lcc['X'] = cts_lcc['geometry'].x.round(2)
cts_lcc['Y'] = cts_lcc['geometry'].y.round(2)
# odbacujemo originalnu geometriju
cts_lcc = cts_lcc.drop(columns='geometry')
print(cts_lcc)
# Lon Lat CITY_NAME CNTRY_NAME X Y
# 0 37.700001 55.749996 Moscow Russia 5646821.07 3516023.12
# 1 -0.178002 51.487911 London UK 3319463.46 2791917.63
# 2 30.249999 59.916663 Saint Petersburg Russia 5094937.76 3806439.07
# 3 13.327569 52.516269 Berlin Germany 4218147.52 2860401.50
# 4 -3.690972 40.442220 Madrid Spain 2867441.74 1658821.40
# 5 12.519999 41.879997 Rome Italy 4204290.37 1713357.25
# 6 30.502107 50.448159 Kyiv Ukraine 5388204.45 2827106.62
# 7 2.432997 48.881997 Paris France 3464710.31 2492467.54
# 8 26.122968 44.430480 Bucharest Romania 5237217.02 2121363.09
# 9 27.575559 53.899938 Minsk Belarus 5106698.74 3136554.55
# 10 10.027998 53.570997 Hamburg Germany 4001793.12 2968918.41
# 11 21.011877 52.244946 Warsaw Poland 4723816.63 2880357.57
# 12 19.094004 47.514996 Budapest Hungary 4660847.20 2358818.72
# 13 2.159001 41.357997 Barcelona Spain 3359415.71 1687220.95
# 14 16.320978 48.202119 Vienna Austria 4453624.50 2411387.37
# 15 36.208305 49.989672 Kharkiv Ukraine 5777199.86 2902542.23
# 16 9.189999 45.473004 Milan Italy 3938581.38 2098630.23
# 17 43.940673 56.289672 Gorkiy Russia 5968174.74 3722088.16
# 18 20.412558 44.799678 Belgrade Serbia 4797138.24 2081947.68
# 19 11.542950 48.140973 Munich Germany 4110994.01 2386560.22Primer 2: Koristeći prethodne podatke i granice država u Evropi kreirati kartu u Lambertovoj konusnoj konformnoj projekciji
library(sf)
library(spData)
cts = st_read("data/cities.csv",
options=c("X_POSSIBLE_NAMES=Lon","Y_POSSIBLE_NAMES=Lat"),
crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
# options: X_POSSIBLE_NAMES=Lon Y_POSSIBLE_NAMES=Lat
# Reading layer `cities' from data source `C:\mk_knjiga\data\cities.csv' using driver `CSV'
# Simple feature collection with 20 features and 4 fields
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: -3.69 ymin: 40.4 xmax: 43.9 ymax: 59.9
# Geodetic CRS: +proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs
lcc_crs = "+proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +units=m" # EPSG:3034, https://epsg.io/3034
cts_lcc = st_transform(cts, crs = lcc_crs)
# koordinate za toponime
ll= st_coordinates(cts_lcc)
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
# izdvojimo okvirno Evropu
sf_use_s2(FALSE)
eur <- st_crop(world, xmin = -20, xmax = 45,
ymin = 30, ymax = 73)
sf_use_s2(TRUE)
eur_lcc = st_transform(eur,
crs = lcc_crs)
# Karta
plot(st_geometry(eur_lcc), graticule = TRUE, col= 'gray',
border ='black', axes = TRUE)
plot(st_geometry(cts_lcc), pch = 20, add = TRUE, col='darkblue')
text(ll[, 1] + 30000, ll[, 2]+ 30000, cts_lcc$CITY_NAME ,col='darkblue',
cex=0.7, pos = 3, offset = 0.1)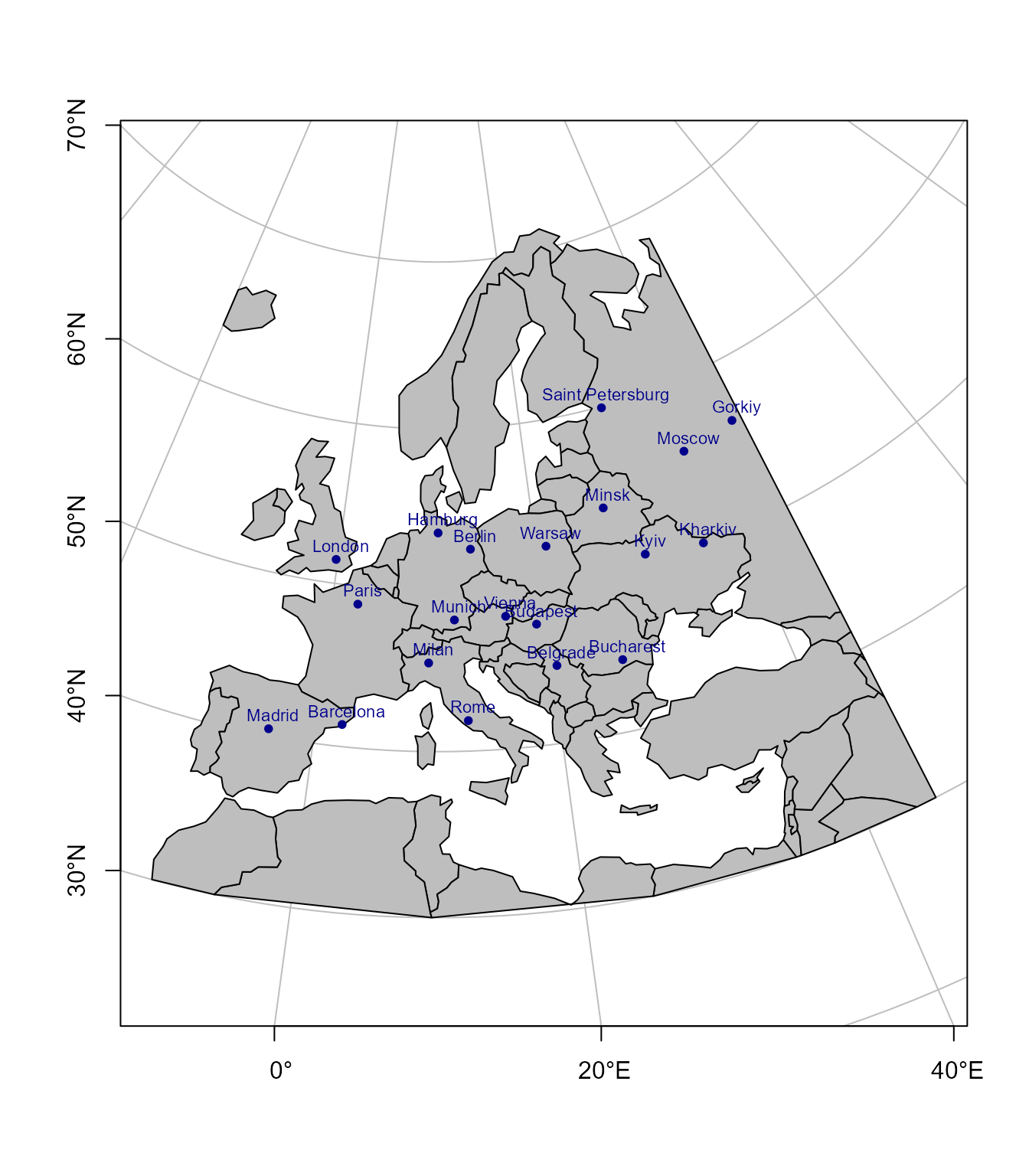
import geopandas as gpd
from shapely.geometry import Point,box
import matplotlib.pyplot as plt
# čitamo podatke iz csv fajla, pokazujemo kolone sa koorsinatama
# definišemo koordinatni referentni sistem (CRS)
cts = gpd.read_file("data/cities.csv" , driver="CSV", X_POSSIBLE_NAMES="Lon", Y_POSSIBLE_NAMES="Lat")
cts.crs = "+proj=longlat +ellps=GRS80 +datum=WGS84"
lcc_crs = "+proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +units=m"
cts = cts.to_crs(crs=lcc_crs)
# Koordinate za toponime
# ll = cts.geometry.apply(lambda geom: (geom.x, geom.y))
cts['X'] = cts['geometry'].x.round(2)
cts['Y'] = cts['geometry'].y.round(2)
# Granice država
# https://github.com/Nowosad/spData/blob/master/inst/shapes/world.gpkg
world = gpd.read_file("data/world.gpkg")
# poligon za clip
polygon = box(-20, 30, 45, 73)
poly_gdf = gpd.GeoDataFrame([1], geometry=[polygon], crs="+proj=longlat +ellps=GRS80 +datum=WGS84")
# eur = world.cx[-20:45, 30:73]
eur = world.clip(poly_gdf)
# C:\Users\user\AppData\Local\Programs\Python\PYTHON~1\lib\site-packages\geopandas\geodataframe.py:2361: UserWarning: CRS mismatch between the CRS of left geometries and the CRS of right geometries.
# Use `to_crs()` to reproject one of the input geometries to match the CRS of the other.
#
# Left CRS: EPSG:4326
# Right CRS: +proj=longlat +ellps=GRS80 +datum=WGS84 +type=crs
#
# return geopandas.clip(self, mask=mask, keep_geom_type=keep_geom_type)
# Obrnuti zatak iz filam u lcc
eur = eur.to_crs(crs=lcc_crs)
# Plot the map
fig, ax = plt.subplots()
eur.boundary.plot(ax=ax, color='gray')
cts.plot(ax=ax, marker='o', color='darkblue')
for x, y, city_name in zip(cts['X'], cts['Y'], cts['CITY_NAME']):
ax.text(x *1.05, y*1.05, city_name, color='darkblue', fontsize=6, ha='right', va='top')
ax.set_aspect('equal')
ax.set_axis_off()
plt.margins(0)
plt.show()
Primer 3: Grafik deformacija u zavisnosti od geodetske širine
Napraviti grafik razmere površina u zavisnosti od geodetske širine u Lambertovoj konusnoj konformnoj projekciji sa dve standardne paralele 35 i 65 stepeni severne geodetske širine.
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# WGS84 a=6378137.0 rf=298.257223563
# 2 linearno nezavisna parametra WGS84 elipsoida
a=6378137.0
rf=298.257223563 # rf=1/f
# geodetksa širine tačaka od 30 do 80 N u radijanima
fi= seq(30,80,by=1) *pi/180
fi1 = 35*pi/180
fi2 = 65*pi/180
# funkcija za poluprečnik krivine prvog vertikala
N = function(fi, a=6378137.0 , rf=298.257223563 ){
# fi u radijanima
f = 1/rf
e = sqrt(2*f - f^2)
N = a / sqrt( 1- e^2 * (sin(fi))^2 )
return(N)
}
# Funkcija za U (kod računanja izometrijske širine)
U = function(fi, a=6378137.0 , rf=298.257223563 ){
# fi u radijanima
f = 1/rf
e = sqrt(2*f - f^2)
psi = asin(e*sin(fi))
U = tan(pi/4+fi/2) / (tan(pi/4 +psi/2))^e
# drugi način
# U= tan(pi/4+fi/2) * ( ( 1- e*sin(fi) ) / ( 1+e * sin(fi) ) )^(e/2)
return(U)
}
# funkcija za konstantu proporcionalnosti
kp = function(fi1, fi2, a=6378137.0 , rf=298.257223563 ){
# fi1 i fi2 u radijanima
r1 = N(fi1)*cos(fi1)
r2 = N(fi2)*cos(fi2)
k= (log(r1) - log(r2) ) / (log(U(fi2)) - log(U(fi1)) )
return(k)
}
# poluprečnik krivine paralele
r <- function(fi){ N(fi)*cos(fi)}
# poluprečnik 1. st. par.
r1 = r(fi1)
# konstanta proporcionalnosti
k = kp(fi1,fi2)
# konstanta integracije
C = (r1* U(fi1)^k ) /k
# test
round(C,1) == round((r(fi2)* U(fi2)^k ) /k , 1)
# [1] TRUE
# linearna razmera
m=n= k* C / (r(fi)*U(fi)^k)
# razmer površina
p=m^2
plot(fi*180/pi,p, main = "Razmer površina u zavisnosti od geod. širine",
xlab = parse(text = "varphi"), ylab = "p",type = "l")
abline(v = 35, col='gray')
abline(v=65, col='gray')
grid()
import numpy as np
import matplotlib.pyplot as plt
# _parametri WGS84 elipsoida
a = 6378137.0
rf = 298.257223563 # rf = 1/f
# Latitude od 30 do 80 N u radijanima
fi = np.arange(30, 81) * np.pi / 180
fi1 = 35 * np.pi / 180
fi2 = 65 * np.pi / 180
# f-ja za radijus krivine prvog vertikala
def N(fi, a=6377397.155, rf=299.1528128):
f = 1 / rf
e = np.sqrt(2 * f - f**2)
N = a / np.sqrt(1 - e**2 * np.sin(fi)**2)
return N
# f-ja za U
def U(fi, a=6377397.155, rf=299.1528128):
f = 1 / rf
e = np.sqrt(2 * f - f**2)
psi = np.arcsin(e * np.sin(fi))
U = np.tan(np.pi / 4 + fi / 2) / np.tan(np.pi / 4 + psi / 2)**e
return U
# f-ja za konstantu proporcionalnosti
def kp(fi1, fi2, a=6377397.155, rf=299.1528128):
r1 = N(fi1) * np.cos(fi1)
r2 = N(fi2) * np.cos(fi2)
k = (np.log(r1) - np.log(r2)) / (np.log(U(fi2)) - np.log(U(fi1)))
return k
# f-ja za radijus krivine paralele
def r(fi):
return N(fi) * np.cos(fi)
# konstanta proporcionalnosti
k = kp(fi1, fi2)
# Konstanta integracije
C = (r(fi1) * U(fi1)**k) / k
# linearna razmera
m = n = k * C / (r(fi) * U(fi)**k)
# razmer površina
p = m**2
# Plot the results
plt.plot(fi * 180 / np.pi, p)
plt.axvline(x=35, color='gray')
plt.axvline(x=65, color='gray')
plt.grid()
plt.xlabel(r'$\varphi$')
plt.ylabel('p')
plt.title('Razmer površina u zavisnosti od geod. širine')
plt.show()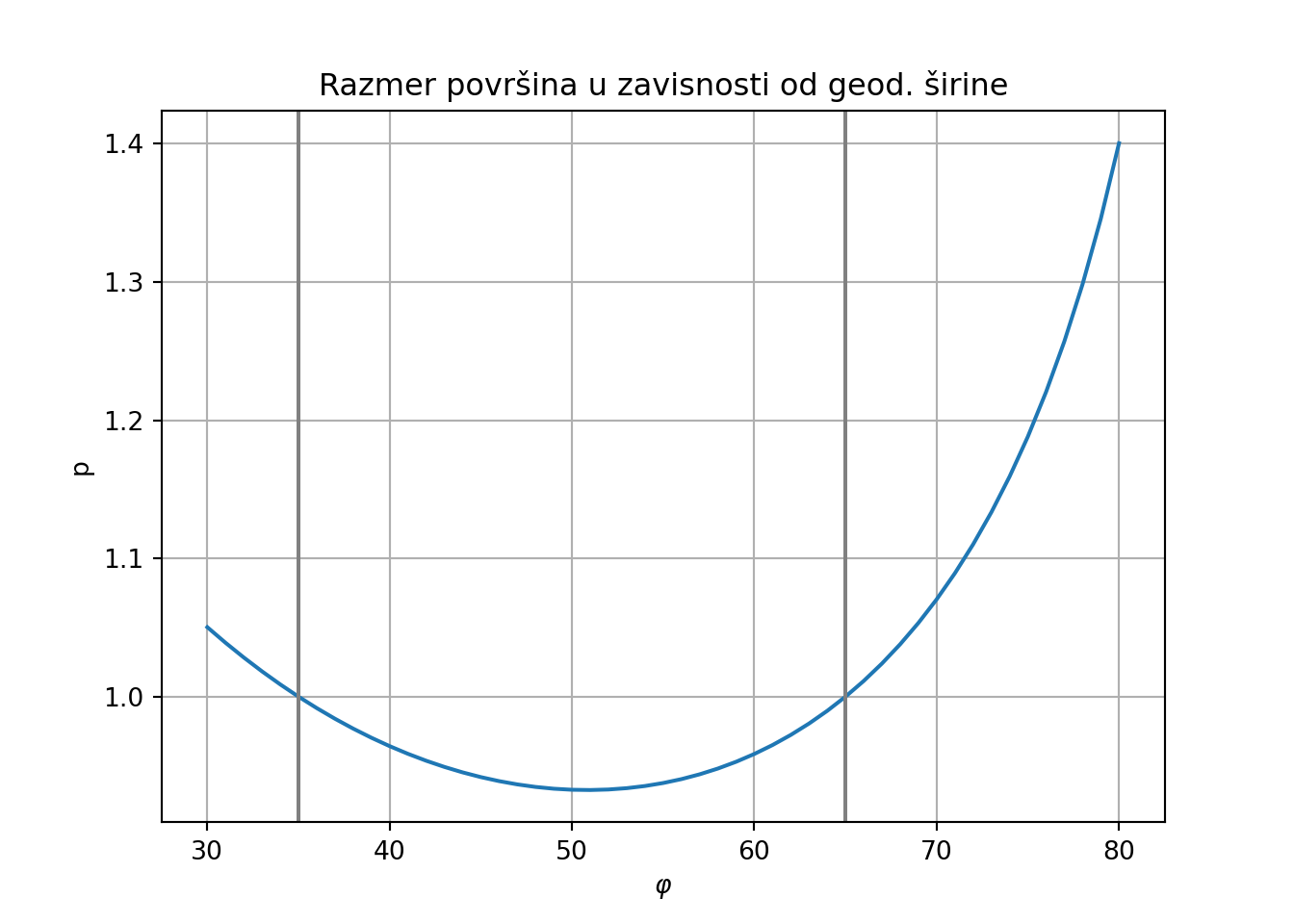
Tabela 5.1 pokazuje linearnu razmeru, linearnu deformaciju, razmer površina i deformaciju površina u zavisnosti od geodetske širine u Lambertovoj konusnoj konformnoj projekciji sa 2 standardne paralele, 35 i 65 stepeni severne geodetske širine.
options( digits = 12)
df =data.frame(Latituda = round(fi*180/pi ),
c = round(sqrt(p), 6),
dc= round(sqrt(p)-1 , 6),
p=round(p, 6),
dp =round(p-1 ,6) )
knitr::kable(df[seq(1,51,by=5), ],align = "c", row.names = FALSE,
format.args = list(scientific = FALSE, format = "f") ) | Latituda | c | dc | p | dp |
|---|---|---|---|---|
| 30 | 1.024816 | 0.024816 | 1.050248 | 0.050248 |
| 35 | 1.000000 | 0.000000 | 1.000000 | 0.000000 |
| 40 | 0.981924 | -0.018076 | 0.964175 | -0.035825 |
| 45 | 0.970451 | -0.029549 | 0.941775 | -0.058225 |
| 50 | 0.965725 | -0.034275 | 0.932625 | -0.067375 |
| 55 | 0.968249 | -0.031751 | 0.937506 | -0.062494 |
| 60 | 0.979046 | -0.020954 | 0.958531 | -0.041469 |
| 65 | 1.000000 | 0.000000 | 1.000000 | 0.000000 |
| 70 | 1.034620 | 0.034620 | 1.070439 | 0.070439 |
| 75 | 1.090021 | 0.090021 | 1.188146 | 0.188146 |
| 80 | 1.183415 | 0.183415 | 1.400472 | 0.400472 |
Primer 4: Inverzni zadatak Lambertova konusna konformna projekcija
Pravougle koordinate u Lambertovoj konusnoj konformnoj projekciji korišćene u Primeru 1 T1(4797138, 2081947) i T2(4110994, 2386560) transformisati na elipsoidne u GS80 sa datumom koji se poklapa sa WGS84. Elipsoidne koordinate izraziti i u obliku stepen, minut i sekund
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Za tacke sa koordinatama T1(4797138, 2081947) i T2(4110994, 2386560) u LCC projekciji
lcc_crs = "+proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +units=m" # EPSG:3034, https://epsg.io/3034
# Sračunaj koordinate na GRS80 elipsoidu
tLCC= st_sfc( st_point(c(4797138, 2081947)), st_point(c(4110994, 2386560)),
crs = lcc_crs )
# inverzni zadatak iz pravouglih u longitudu, latitudu
tLL = st_transform(tLCC,
crs = "+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
ll = st_coordinates(tLL)
# Koordinate treba zaokružiti do na cm ili dm, što je oko 6. decimale
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
round(ll,6)
# X Y
# [1,] 20.412554 44.799672
# [2,] 11.542950 48.140971
# gedetska dužina i širina
# lon lat
lon = ll[,1]
lat = ll[,2]
# funkcija za stepen u stepen minut sekund
deg2dms <- function(deg){
deg_sign = sign(deg)
deg = abs(deg)
DEG = floor(deg)
MIN = floor((deg - DEG) * 60)
SEC = (deg - DEG - MIN/60) * 3600
SEC=round(SEC,2)
dms=paste(deg_sign*DEG,'\u00B0',MIN,"'",SEC,"''",sep='')
return(dms)
}
# gedetska dužina i širina
print(paste("T1 " ,deg2dms(lon[1]), deg2dms(lat[1])) )
# [1] "T1 20°24'45.19'' 44°47'58.82''"
print(paste( "T2 " ,deg2dms(lon[2]), deg2dms(lat[2])) )
# [1] "T2 11°32'34.62'' 48°8'27.5''"import shapely.geometry
import geopandas as gpd
# pravimo GeoDataFrame koordinate u LCC projekciji
data = {'geometry': [shapely.geometry.Point(4797138, 2081947), shapely.geometry.Point(4110994, 2386560)]}
lcc_crs = "+proj=lcc +lat_1=35 +lat_2=65 +lat_0=52 +lon_0=10 +x_0=4000000 +y_0=2800000 +ellps=GRS80 +units=m" #
gdf = gpd.GeoDataFrame(data, crs=lcc_crs) # LCC
# transformacija u GRS80
gdf_grs80 = gdf.to_crs("+proj=longlat +ellps=GRS80 +datum=WGS84 +no_defs")
print(gdf_grs80)
# geometry
# 0 POINT (20.41255 44.79967)
# 1 POINT (11.54295 48.14097)
# Prikaz koordinata na 6 decimala
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
lon = gdf_grs80["geometry"].x
lat = gdf_grs80["geometry"].y
# gedetska dužina i širina
print("T1 " ,round(lon[0],6), round(lat[0],6))
# T1 20.412554 44.799672
print("T2 " ,round(lon[1],6), round(lat[1],6))
# T2 11.54295 48.140971
# funkcija za stepen u stepen minut sekund
def deg2dms(deg):
deg_sign = 1 if deg >= 0 else -1
deg = abs(deg)
DEG = int(deg)
MIN = int((deg - DEG) * 60)
SEC = (deg - DEG - MIN / 60) * 3600
SEC = round(SEC, 2)
dms = f"{deg_sign*DEG}\u00B0{MIN}'{SEC}''"
return dms
# gedetska dužina i širina
print(f"T1 {deg2dms(lon[0])} {deg2dms(lat[0])}")
# T1 20°24'45.19'' 44°47'58.82''
print(f"T2 {deg2dms(lon[1])} {deg2dms(lat[1])}")
# T2 11°32'34.62'' 48°8'27.5''