9 Pregled nekih značajnih globalnih projekcija
Ovo poglavlje prikazuje različite vrste kartografskih projekcija koje nisu bile obuhvaćene u dosadašnjem delu knjige. Prikazano je nekoliko tipova projekcija, uključujući polikonusne, pseudokonusne i pseudocilindrične projekcije. Takođe se razmatraju specifične projekcije kao što su Van der Griten projekcija, Robinsonova projekcija i Ekui7Grid.
9.1 Polikonusne projekcije
Pri razmatranju prostih konusnih projekcija na dodirnom konusu konstatovali smo da se udaljavanjem od dodirne paralele razmeri koji se odnose na pojedine paralele neprekidno menjaju (povećavaju). Ako se teritorija proteže po širini, onda će se na krajnjim paralelama linearni razmer znatno razlikovati od glavnog razmera. Iz istih razloga nastala je zamisao da se sve paralele karte učine dodirnim, tj. da se projiciranje vrši ne na jedan konus, već na više konusa, otuda i naziv polikonusne projekcije (Jovanović 1984).
Opšte jednačine polikonusnih projekcija (Jovanović 1984):
- \(x=q-\rho \cos \delta\)
- \(y=\rho \sin \delta\)
- \(\rho=f_1(\varphi)\)
- \(\delta=f_2(\varphi, \lambda)\)
- \(q=f_3(\varphi)\)
- \(\tan \varepsilon=-\frac{\sin \delta \frac{d q}{d \varphi}+\rho \frac{\partial \delta}{\partial \varphi}}{\cos \delta \frac{d q}{d \varphi}-\frac{d \rho}{d \varphi}}\)
- \(p=\rho \frac{\partial \delta}{\partial \lambda} \frac{\left(\cos \delta \frac{d q}{d \varphi}-\frac{d \rho}{d \varphi}\right)}{M r}\)
- \(n=\frac{\rho}{r} \frac{\partial \delta}{\partial \lambda}\)
- \(m=\frac{p}{n} \sec \delta=\frac{\cos \frac{d q}{d \varphi}-\frac{d \rho}{d \varphi}}{M}\)
- \(\tan \frac{\omega}{2}=\frac{1}{2} \sqrt{\frac{m^2+n 2-2 p}{p}}\).
Osobine (Snyder (1987)):
Uslovna je projekcija.
Paralele (osim za Ekvator) su lukovi krugova, ali nisu koncentrični.
Centralni meridijan i Ekvator su prave linije; svi ostali meridijani su složene krive.
Nema deformacije dužina duž svake paralele i duž centralnog meridijana, u ovoj projekciji nema standardne paralele.
Koristi se skoro isključivo u blago modifikovanom obliku za kartiranje velikih razmera.
Prosta (Američka) polikonusna projekcija
Ovu projekciju po prvi put je razradio i predložio 1820. godine profesor Ferdinand Hassler, organizator i prvi direktor službe obalskog premera SAD (US Coast Survey). Kasnije je teoriju iste projekcije definitivno obradio poznati američki geodeta Adams i objavio 1920. Sledeći primer pokazuje kartu u Prostoj (Američkoj) polikonusnoj projekciji sa približnim elipsama deformacija, Slika 9.2.
library(sf)
library(spData)
# Koordinate za elipse deformacija
l = seq(-150,150, by=50)
f = seq(-80,80, by=20) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +ellps=GRS80")
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u poly projekciji
poly_crs = "+proj=poly"
tissot.poly <- st_transform(tissot.sf, poly_crs)
# površine u projekciji
tissot.poly$a_proj <- st_area(tissot.poly)
# odnos površina u projekciji i na sferi
tissot.poly$p <- tissot.poly$a_proj/tissot.poly$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_poly = st_transform(world, crs = poly_crs)
ll = st_centroid(tissot.poly)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_poly),
col= 'gray', border ='black', axes = TRUE)
plot(st_geometry(tissot.poly),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.poly$p,1)) ,col='red' , cex = 0.8)
9.2 Pseudokonusne projekcije
Paralele normalne mreže su koncentrični krugovi, kao i kod konusnih projekcija, dok su meridijani lukovi proizvoljnih krivih simetrično razmešteni oko slika srednjeg meridijana, koji se preslikava kao prava linija. Zemljini polovi preslikavaju se u tačke.
Pri izvođenju jednačina pseudokonusnih projekcija, kao i kod običnih konusnih projekcija, primenjuju se polarne i pravougle koordinate u ravni.
Opšte jednačine pseudokonusnih projekcija (Jovanović 1984):
- \(\rho=f_1(\varphi)\)
- \(\delta=f_2(\varphi, \lambda)\)
- \(q=\) const.
- \(x=q-\rho \cos \delta\)
- \(y=\rho \sin \delta\)
- \(\tan \varepsilon=\frac{\frac{\partial \delta}{\partial \varphi}}{\frac{d \rho}{d \varphi}}\)
- \(m=-\frac{\frac{d \rho}{d \varphi}}{M} \sec \varepsilon\)
- \(n=\frac{\rho}{r} \frac{\partial \delta}{\partial \lambda}\)
- \(p=-\frac{\rho}{M r} \frac{d \rho}{d \varphi} \frac{\partial \delta}{\partial \lambda}\)
- \(\tan \frac{\omega}{2}=\frac{1}{2} \sqrt{\frac{m^2+n^2}{p}-2}\)
- \(a=\frac{1}{2}(A+B), b=\frac{1}{2}(A-B)\) \(A=\sqrt{m^2+n^2+2 p}, B=\sqrt{m^2+n^2-2 p}\).
Boneove projekcije
Osobine Boneove projekcije (Snyder 1987):
- Pseudokonusna je i ekvivalentna.
- Centralni meridijan je prava linija. Ostali meridijani su složene krive.
- Paralele su koncentrični kružni lukovi, a polovi su tačke.
- Nema deformacija dužina duž centralnog meridijana i svih paralela.
- Nema deformacija dužina duž centralnog meridijana i duž standardne paralele.
- Koristi se za atlas karte kontinenata i za topografsko kartiranje nekih zemalja.
- Sinusoidna projekcija je ekvatorijalni granični oblik Boneove projekcije.
- U velikoj meri koristi se Boneova projekcija od sredine 18. veka.
Sledeći primer pokazuje kartu u Boneovoj projekciji sa približnim elipsama deformacija, Slika 9.3.
library(sf)
library(spData)
# Koordinate za elipse deformacija
l = seq(-150,150, by=50)
f = seq(-80,80, by=20) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +ellps=GRS80") # sfera R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u bonnegle point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u bonne projekciji
bonne_crs = "+proj=bonne +lat_1=10"
tissot.bonne <- st_transform(tissot.sf, bonne_crs)
# površine u projekciji
tissot.bonne$a_proj <- st_area(tissot.bonne)
# odnos površina u projekciji i na sferi
tissot.bonne$p <- tissot.bonne$a_proj/tissot.bonne$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_bonne = st_transform(world, crs = bonne_crs)
ll = st_centroid(tissot.bonne)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_bonne), graticule=T,
col= 'gray', border ='black', axes = F)
plot(st_geometry(tissot.bonne),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.bonne$p,1)) ,col='red' , cex = 0.8)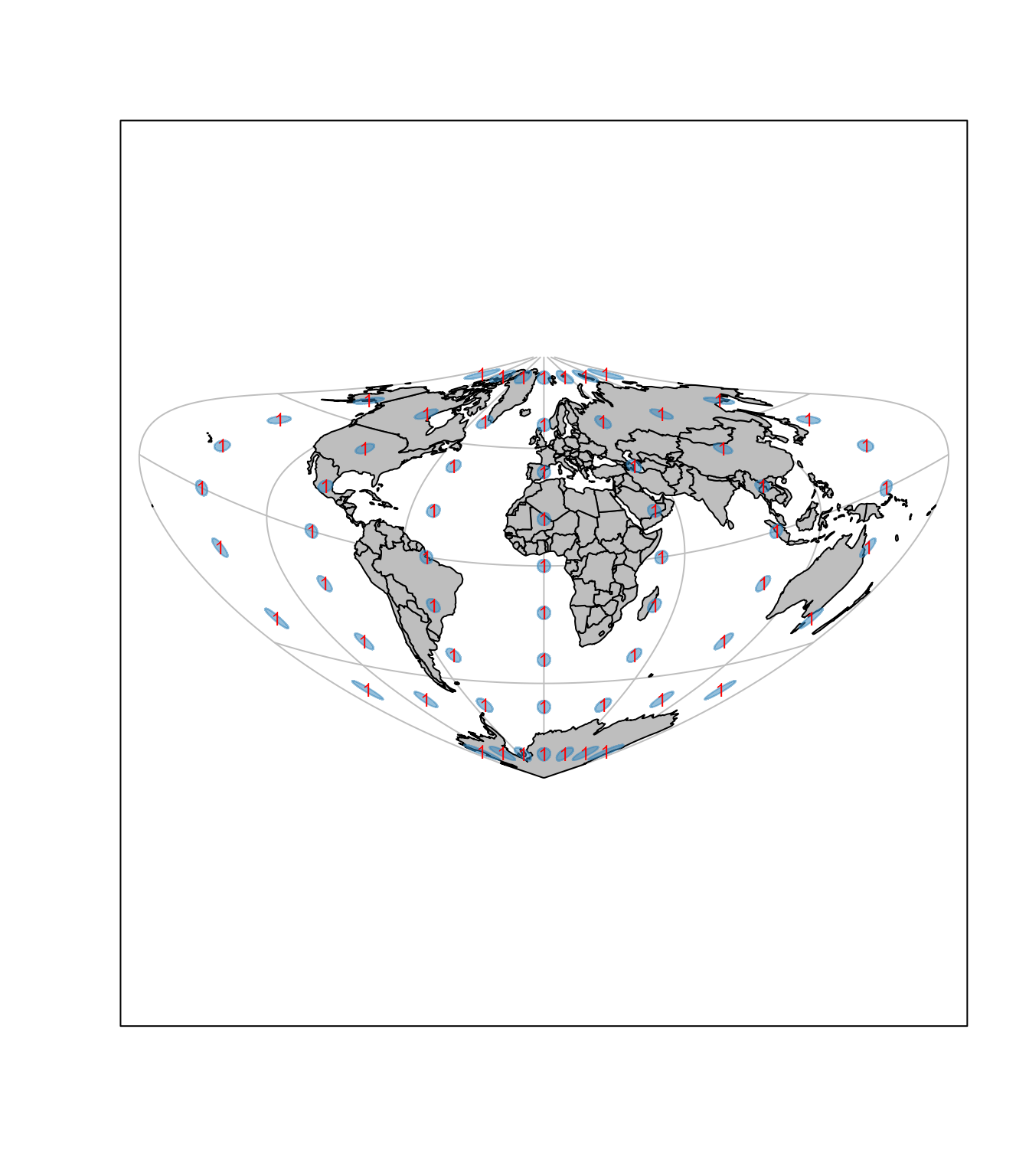
9.3 Pseudocilindrične projekcije
Slike paralela u pseudokonusnim projekcijama su lukovi koncentričnih krugova, čiji centar leži na projekciji srednjeg meridijana. Od svih meridijana jedino se srednji meridijan preslikava kao prava linija. Slike ostalih meridijana su krive linije simetrične u odnosu na srednji meridijan.
Pri izvođenju jednačina pseudokonusnih projekcija, kao i kod običnih konusnih projekcija, primenjuju se polarne i pravougle koordinate u ravni.
Opšte jednačine pseudocilindričnih projekcija (Jovanović 1984):
- \(x=f_1(\varphi)\)
- \(y=f_2(\varphi, \lambda)\)
- \(\tan \varepsilon=-\frac{\frac{\partial y}{\partial \varphi}}{\frac{d x}{d \varphi}}\)
- \(m=\frac{\frac{d x}{d \varphi}}{M} \sec \varepsilon\)
- \(n=\frac{\frac{\partial y}{\partial \lambda}}{N} \sec \varphi\)
- \(p=\frac{\frac{d x}{d \varphi} \frac{\partial y}{\partial \lambda}}{M N} \sec \varphi\)
- \(\sin \frac{\omega}{2}=\sqrt{\frac{m^2+n^2-2 p}{m^2+n^2+2 p}}\) ili \(\tan \frac{\omega}{2}=\frac{1}{2} \sqrt{\frac{m^2+n^2-2 p}{p}}\).
Sansonova ili Sinusoidalna projekcija
Osobine Sansonove projekcije (Snyder (1987)):
Pseudocilindrična projekcija.
Ekvivalenta je projekcija.
Centralni meridijan je prava linija; svi ostali meridijani su prikazani kao podjednako razmaknute sinusoidne krive.
Paralele su jednako raspoređene prave, paralelne jedna drugoj.
Nema deformacija dužina duž centralnog meridijana i svih paralela.
Koristi se za karte sveta sa jednim centralnim meridijanom ili u isprekidanom obliku sa nekoliko centralnih meridijana.
Koristi se za satelitske podatke MODIS misije.
Koristi se od sredine 16. veka.
Sledeći primer pokazuje kartu u Sinusoidnoj projekciji sa približnim elipsama deformacija, Slika 9.4.
library(sf)
library(spData)
# Koordinate za elipse deformacija
l = seq(-150,150, by=50)
f = seq(-80,80, by=20) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +ellps=GRS80") # sfera R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u sin projekciji
sin_crs = "+proj=sinu"
tissot.sin <- st_transform(tissot.sf, sin_crs)
# površine u projekciji
tissot.sin$a_proj <- st_area(tissot.sin)
# odnos površina u projekciji i na sferi
tissot.sin$p <- tissot.sin$a_proj/tissot.sin$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_sin = st_transform(world, crs = sin_crs)
ll = st_centroid(tissot.sin)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_sin), graticule=T,
col= 'gray', border ='black', axes = F)
plot(st_geometry(tissot.sin),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.sin$p,1)) ,col='red' , cex = 0.8)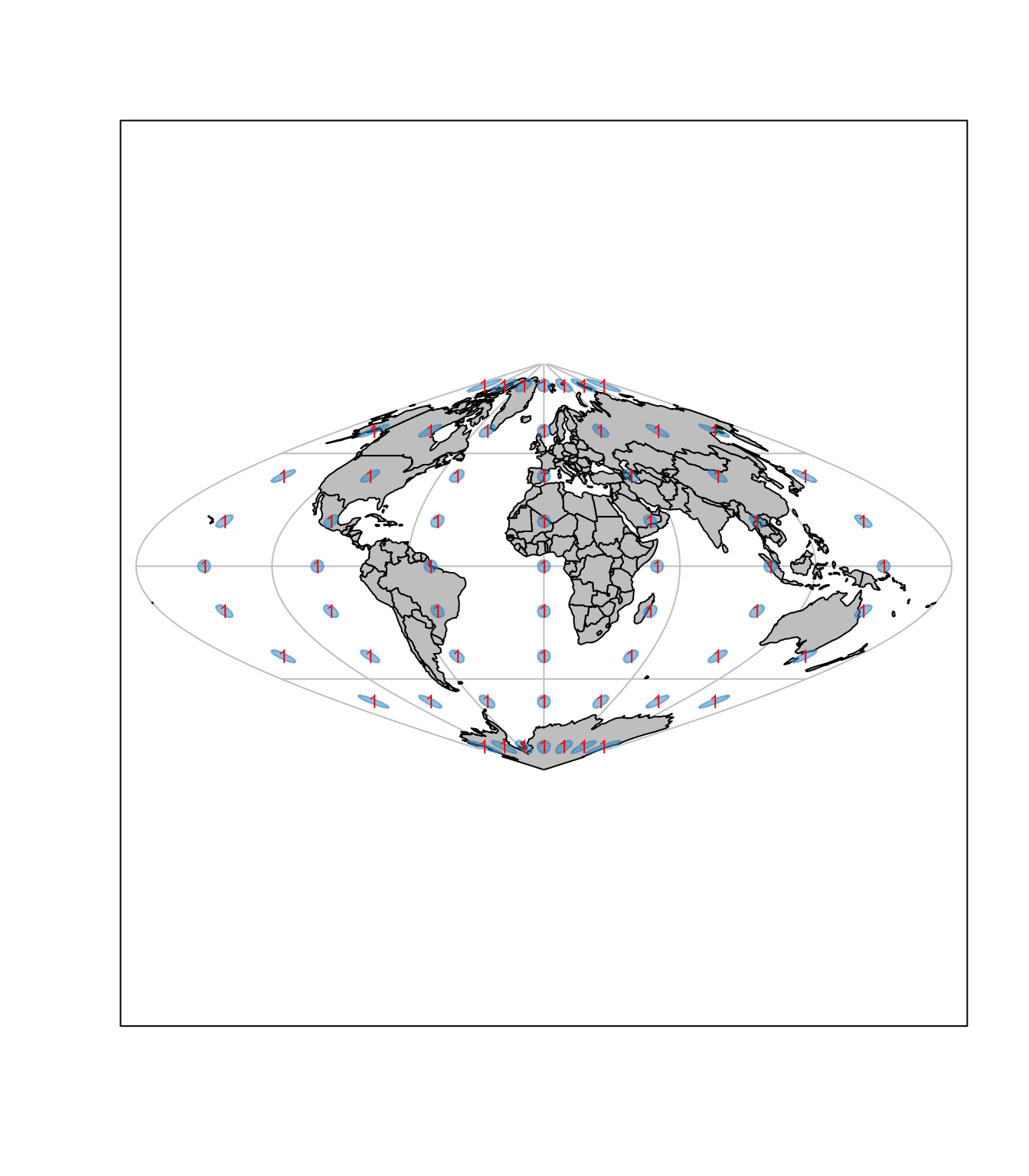
Molvajdova (Mollweide) eliptična projekcija
Osobine Molvajdove projekcije (Snyder 1987):
Ekvivalentna je.
Centralni meridijan je prava linija; 90. meridijani su kružni lukovi; svi ostali meridijani su jednako raspoređeni eliptični lukovi.
Paralele su nejednako raspoređene prave, paralelne jedna sa drugom.
Nema deformacije dužina duž geografskih širina \(40^o44'\) severno i južno.
Koristi se za karte sveta.
Inspiracija za nekoliko drugih projekcija.
Predstavio je Molvajd 1805. godine.
Sledeći primer pokazuje kartu u Sinusoidnoj projekciji sa približnim elipsama deformacija, Slika 9.5.
library(sf)
library(spData)
# Koordinate za elipse deformacija
l = seq(-150,150, by=50)
f = seq(-80,80, by=20) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +ellps=GRS80") # sfera R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u moll projekciji
moll_crs = "+proj=moll"
tissot.moll <- st_transform(tissot.sf, moll_crs)
# površine u projekciji
tissot.moll$a_proj <- st_area(tissot.moll)
# odnos površina u projekciji i na sferi
tissot.moll$p <- tissot.moll$a_proj/tissot.moll$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_moll = st_transform(world, crs = moll_crs)
ll = st_centroid(tissot.moll)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_moll), graticule=T,
col= 'gray', border ='black', axes =F)
plot(st_geometry(tissot.moll),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.moll$p,1)) ,col='red' , cex = 0.8)
9.4 Van der Gritenova projekcija
Osobine Van der Gritenove projekcije (Snyder (1987)):
Uslovna. Nije pseudocilindrična.
Prikazuje ceo globus zatvoren u krug.
Centralni meridijan i ekvator su prave linije.
Svi ostali meridijani i paralele su lukovi kružnica.
Zakrivljena modifikacija Merkatorove projekcije, sa velikim izobličenjem u polarnim oblastima.
Ekvator se preslikava bez deformacija.
Koristi se za karte sveta.
Koristi se samo u sfernom obliku.
Predstavio Van der Grinten 1904. godine.
Sledeći primer pokazuje kartu u Van der Gritenovoj projekciji sa približnim elipsama deformacija, Slika 9.6.
library(sf)
library(spData)
# Koordinate za elipse deformacija
l = seq(-150,150, by=50)
f = seq(-80,80, by=20) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +ellps=GRS80") # sfera R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u vdg projekciji
vdg_crs = "+proj=vandg +R_A +lon_0=0 +x_0=0 +y_0=0 +R=6371000 +units=m +no_defs +type=crs"
tissot.vdg <- st_transform(tissot.sf, vdg_crs)
# površine u projekciji
tissot.vdg$a_proj <- st_area(tissot.vdg)
# odnos površina u projekciji i na sferi
tissot.vdg$p <- tissot.vdg$a_proj/tissot.vdg$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_vdg = st_transform(world, crs = vdg_crs)
ll = st_centroid(tissot.vdg)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_vdg), graticule=T,
col= 'gray', border ='black', axes =F)
plot(st_geometry(tissot.vdg),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.vdg$p,1)) ,col='red' , cex = 0.8)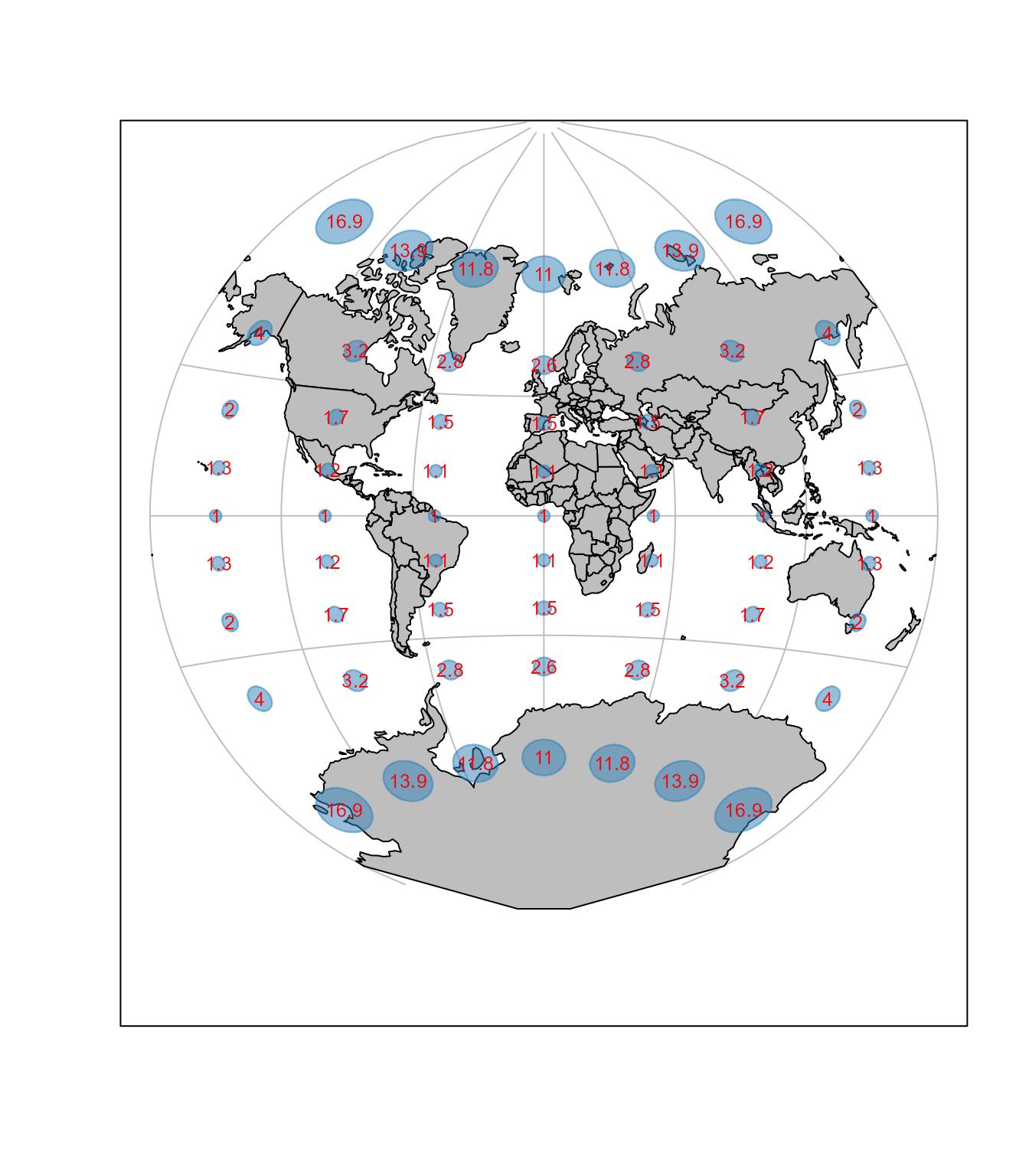
9.5 Robinsonova projekcija
Robinsonovu projekciju je osmislio Artur H. Robinson 1963. godine kao odgovor na apel kompanije Rand McNalli, koja je od tog vremena koristila projekciju u kartama sveta opšte namene. Robinson je 1974. godine objavio detalje o konstrukciji projekcije. Nacionalno geografsko društvo (NGS) je počelo da koristi Robinsonovu projekciju za karte sveta opšte namene 1988. godine, zamenivši Van der Grintenovu projekciju.
Sledeći primer pokazuje kartu u Robinsonovoj projekciji sa približnim elipsama deformacija, Slika 9.7.
library(sf)
library(spData)
# Koordinate za elipse deformacija
l = seq(-150,150, by=50)
f = seq(-80,80, by=20) #seq(20,90,by=10)
m = c()
# matrica lokacija elipsi
for(i in f){
m = rbind(m,cbind(l,rep(i,length(l))))
}
# kreiramo tačke u kojima cemo prikazati elipse deformacija
tissot.pt <- st_sfc( st_multipoint(m ),
crs = "+proj=longlat +ellps=GRS80") # sfera R=6377 km
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# R = 300 km
tissot.sf = st_buffer(tissot.pt, dist = 300000, max_cells = 1000)
# sf obj
tissot.sf <- st_sf( tissot.sf)
# Sračunajmo površinu svakog kruga na sferi
tissot.sf$a <- st_area(tissot.sf)
# transformacija poligona elipsi u rob projekciji
rob_crs = "+proj=robin"
tissot.rob <- st_transform(tissot.sf, rob_crs)
# površine u projekciji
tissot.rob$a_proj <- st_area(tissot.rob)
# odnos površina u projekciji i na sferi
tissot.rob$p <- tissot.rob$a_proj/tissot.rob$a
# granice država
data(world)
granicaSRKS = st_union(world[173, 'geom' ], world[175,'geom'] )
world[173, ]$geom = granicaSRKS$geom
world = world[-175,]
w_rob = st_transform(world, crs = rob_crs)
ll = st_centroid(tissot.rob)
ll = st_coordinates(ll)
# Karta sa elipsama deformacija i razmerom površina
plot(st_geometry(w_rob), graticule=T,
col= 'gray', border ='black', axes = T)
plot(st_geometry(tissot.rob),
border = rgb(44/255,127/255,184/255,0.5),col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste(round(tissot.rob$p,1)) ,col='red' , cex = 0.8)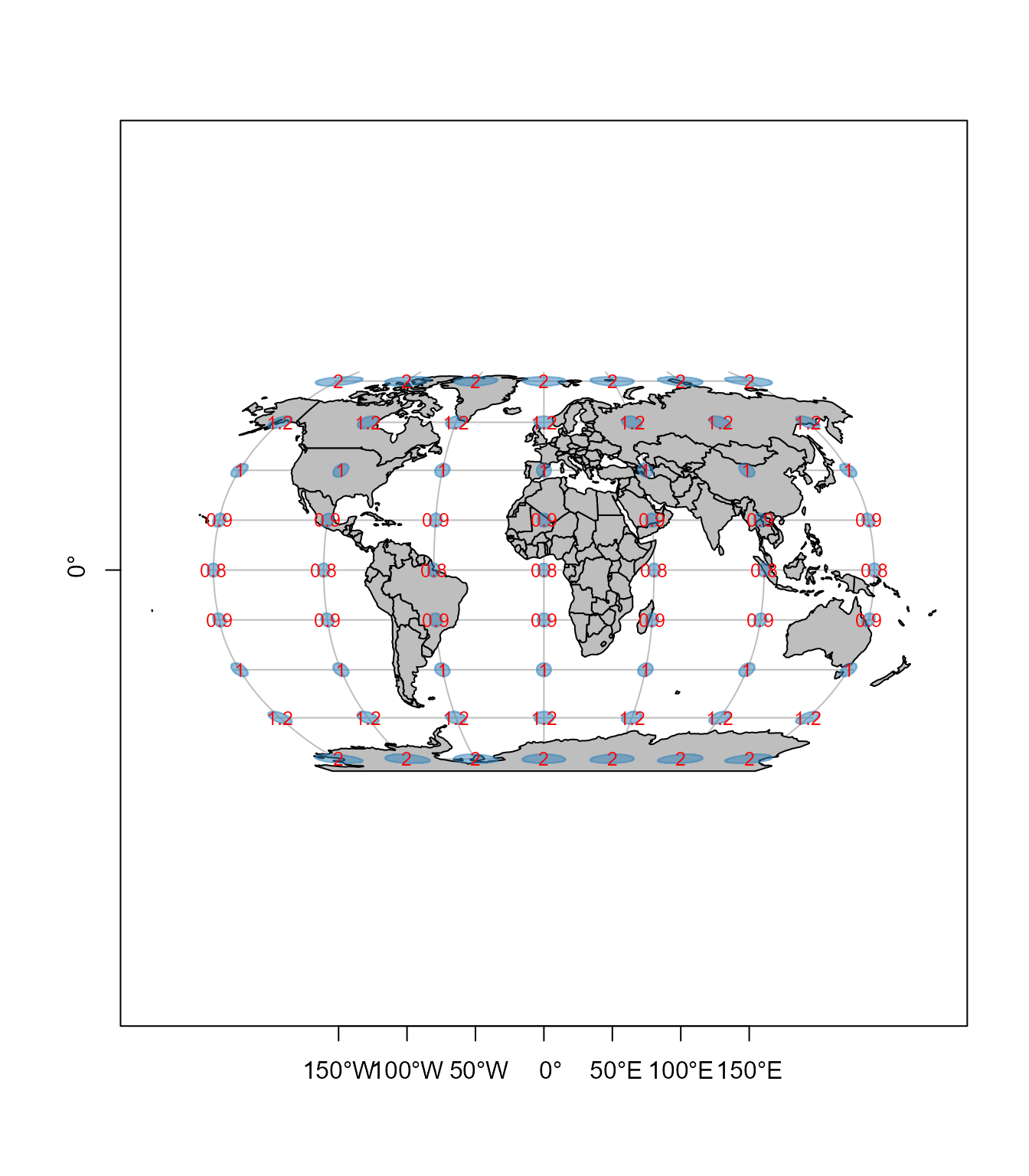
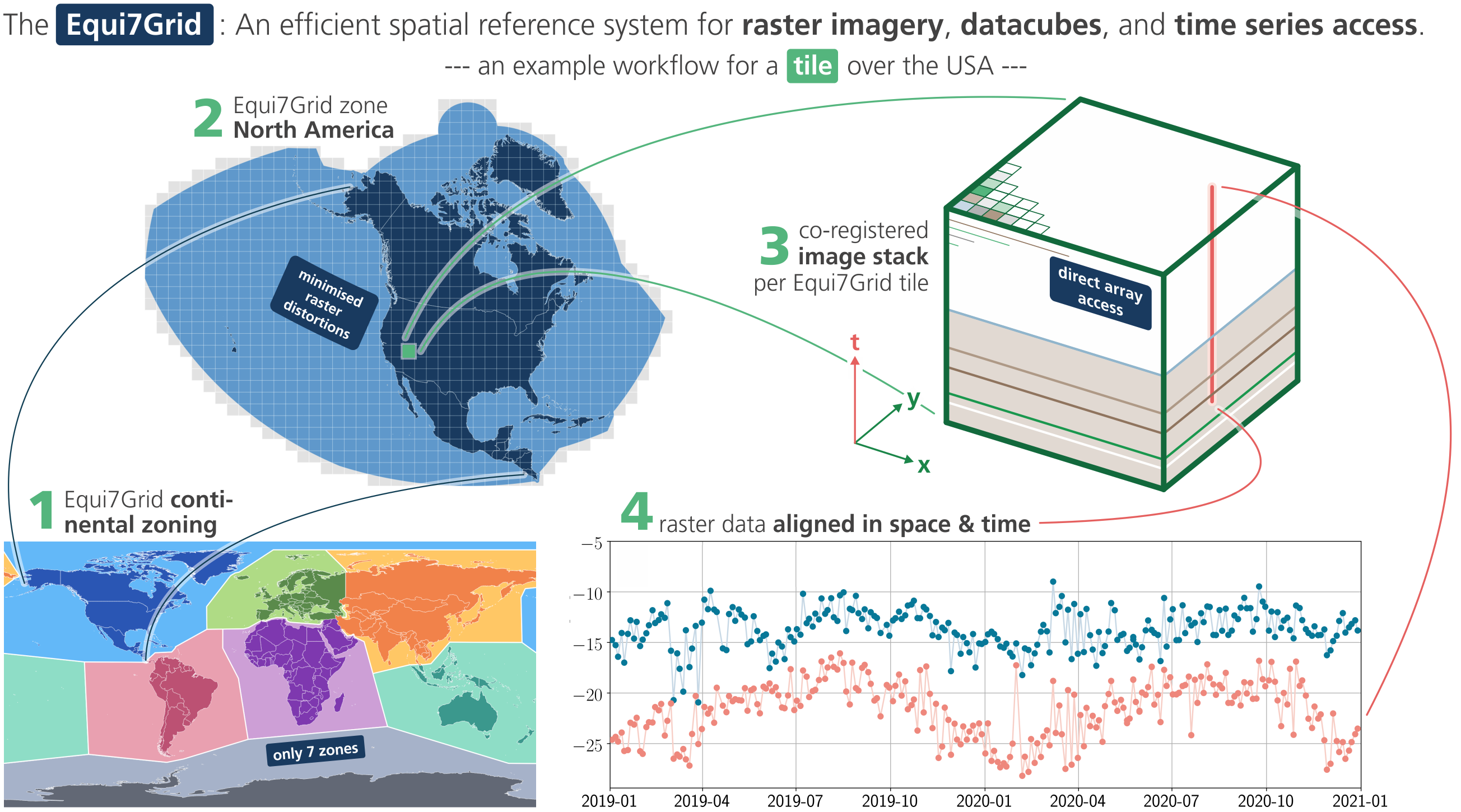
9.6 Ekui7Grid
Ekui7Grid je prostorni referentni sistem dizajniran da efikasno upravlja arhiviranjem, obradom i prikazom prostornih rastera visoke rezolucije. Podržava prostorno vremenske rasterske podatke koji sadrže velike količine satelitskih snimaka, pošto čuva geometrijsku tačnost i minimizira osnovno uzorkovanje/opažanje po lokaciji na globalnim kopnenim površinama na veoma nisku vrednost od 3%, da se ne dešava da se neki pikseli kod satelitskih snimaka čuvaju više puta. Dakle, minimizuje se broj piksela za koje se čuvaju podaci u npr. dva susedna tajla, kod Sentinel podataka postoji preklop između tajlova pa se pikseli čuvaju u 2 susedna tajla, slično se dešava kod granmularnog čuvanja Sentinel 2 snimaka. Kod UTM projekcije kao što smo videli preklop između tajlova je 40 km, kod granularnog grida preklop je oko 9.8 km, videti više na https://sentinels.copernicus.eu/web/sentinel/missions/sentinel-2/data-products.
Bauer-Marschallinger, Sabel, and Wagner (2014) predlažu Ekui7Grid sistem za satelitske snimke visoke rezolucije koji je kompozicija više projekcija. Za podatke daljinske detekcije visoke rezolucije, standardni gridovi za podatke definisani kartografskim projekcijama su primenjivani kao izvodljivi, svesni njihovih nedostataka zbog deformacija koje su karakteristične za sve projekcije, i preklopima koji se pojavljuju kao npr. kod UTM grid sistema. Bauer-Marschallinger, Sabel, and Wagner (2014) definisali su novu metriku pod nazivom faktor ponovnog uzorkovanja grida (GOF- grid oversampling factor)koja procenjuje preklop i ponovno uzorkovanje piksela, lokalnih podataka koji se javljaju tokom projekcije snimaka u regularan grid standardnih projekcija. Na osnovu standardnih kartografskih projekcija, oni su definisali skupove prostornih gridova optimizovanih da minimiziraju preklope opaženih lokacijam, piksela, za ceo Svet. Svojim predlogom osiguravaju da se neopžanje ne može dogoditi ni na jednoj lokaciji, dakle nema piksela za koji se ne čuvaju podaci. Iz vrednosti mere GOF zaključili su da su ekvidistantne projekcije najpogodnije za gridove satelitskih opažanja visoke rezolucije i uveden je grid sistem od sedam kontinentalnih gridova (uveden pod imenom Ekui7Grid).
Grid sistem je sastavljen od Azimutne ekvidistantne projekcije koja za svaki kontinent ima optimalne parametre:
AF: '+proj=aeqd +lat_0=8.5 +lon_0=21.5 +x_0=5621452.01998 +y_0=5990638.42298 +datum=WGS84 +units=m +no_defs'
AN: '+proj=aeqd +lat_0=-90 +lon_0=0 +x_0=3714266.97719 +y_0=3402016.50625 +datum=WGS84 +units=m +no_defs'
AS: '+proj=aeqd +lat_0=47 +lon_0=94 +x_0=4340913.84808 +y_0=4812712.92347 +datum=WGS84 +units=m +no_defs'
EU: '+proj=aeqd +lat_0=53 +lon_0=24 +x_0=5837287.81977 +y_0=2121415.69617 +datum=WGS84 +units=m +no_defs'
NA: '+proj=aeqd +lat_0=52 +lon_0=-97.5 +x_0=8264722.17686 +y_0=4867518.35323 +datum=WGS84 +units=m +no_defs'
OC: '+proj=aeqd +lat_0=-19.5 +lon_0=131.5 +x_0=6988408.5356 +y_0=7654884.53733 +datum=WGS84 +units=m +no_defs'
SA: '+proj=aeqd +lat_0=-14 +lon_0=-60.5 +x_0=7257179.23559 +y_0=5592024.44605 +datum=WGS84 +units=m +no_defs'Koncept Ekui7Grida je prikazan na slici (Slika 9.8).
Preporuka za dalje čitanje je rad Bauer-Marschallinger and Falkner (2023) gde su date alternative za skladištenje Sentinel podataka uzimajući u obzir preklope koji nastaju kod korišćenja UTM sistema granulacije za Sentinel podatke. Alternative u smislu efikasnosti skladištenja velikih količina podataka koje isporučuje Sentinel 2 misija su Sinusoidna projekcija koju koristi NASA za MODIS podatke ili Equi7Grid (https://github.com/TUW-GEO/Equi7Grid).
Nestorov (1996) se bavio eksperimentalnim ispitivanjem na temu primene novih adaptabilnih konformnih projekcija, praktičan primer eksperimenta za područje Evrope iznet je u radu (Nestorov, Kilibarda, and Protić 2020).