
7 Gaus-Krigerova projekcija
Gaus-Krigerova projekcija je poprečno-cilindrična projekcija, gde se preslikava uska meridijanska zona, Slika 7.1, projekcija je višezona.
Gaus-Krigerova projekcija zadovoljava sledeće uslove:
- konformna je projekcija,
- srednji meridijan se preslikava kao prava linija (apscisa (x) pravouglog koordinatnog sistema u ravni),
- linearna razmera duž srednjeg meridijna je konstantna i jednaka jedinici,
- Ekvator se preslikava kao prava linija upravna na srednji meridijan i predstavlja ordinatnu osu (y) pravouglog koordinatnog sistema u ravni,
- ostali meridijani preslikavaju se kao krive linije simetrične u odnosu na srednji meridijan,
- slike paralela su krive linije simetrične u odnosu na Ekvator,
- sa obzirom na konformnost preslikavanja koordinatna mreža mora biti ortogonalna.
7.1 Osnovne jednačine direktnog preslikavanja
Izvođenje formula za Gaus-Krigerovu projekciju može se naći u raznoj literaturi na srpskom (i hrvatskom) jeziku (Živković (1972), Borčić (1976), Jovanović (1984)). Detaljno izvođenje dato je i u inostranoj literaturi, kao npr. Krakiwsky (1973).
Pravi zadatak podrazumeva da se na osnovu zadatih uslova odrede ekspilcitni oblici funkcija preslikavanja obrtnog elipsoida na ravan, odnosno eksplicitni oblici funkcija:
\[ x=x(\varphi, \lambda) \]
\[ y=y(\varphi, \lambda) \]
Dakle, na osnovu geografskih koordinata \((\varphi, \lambda)\) proizvoljne tačke na obrtnom elipsoidu treba odrediti eksplicitne formule za računanje pravouglih koordinata (\(x,y\)) korespodentne tačke (njene slike) u ravni.
Opšta formula za linearnu razmeru
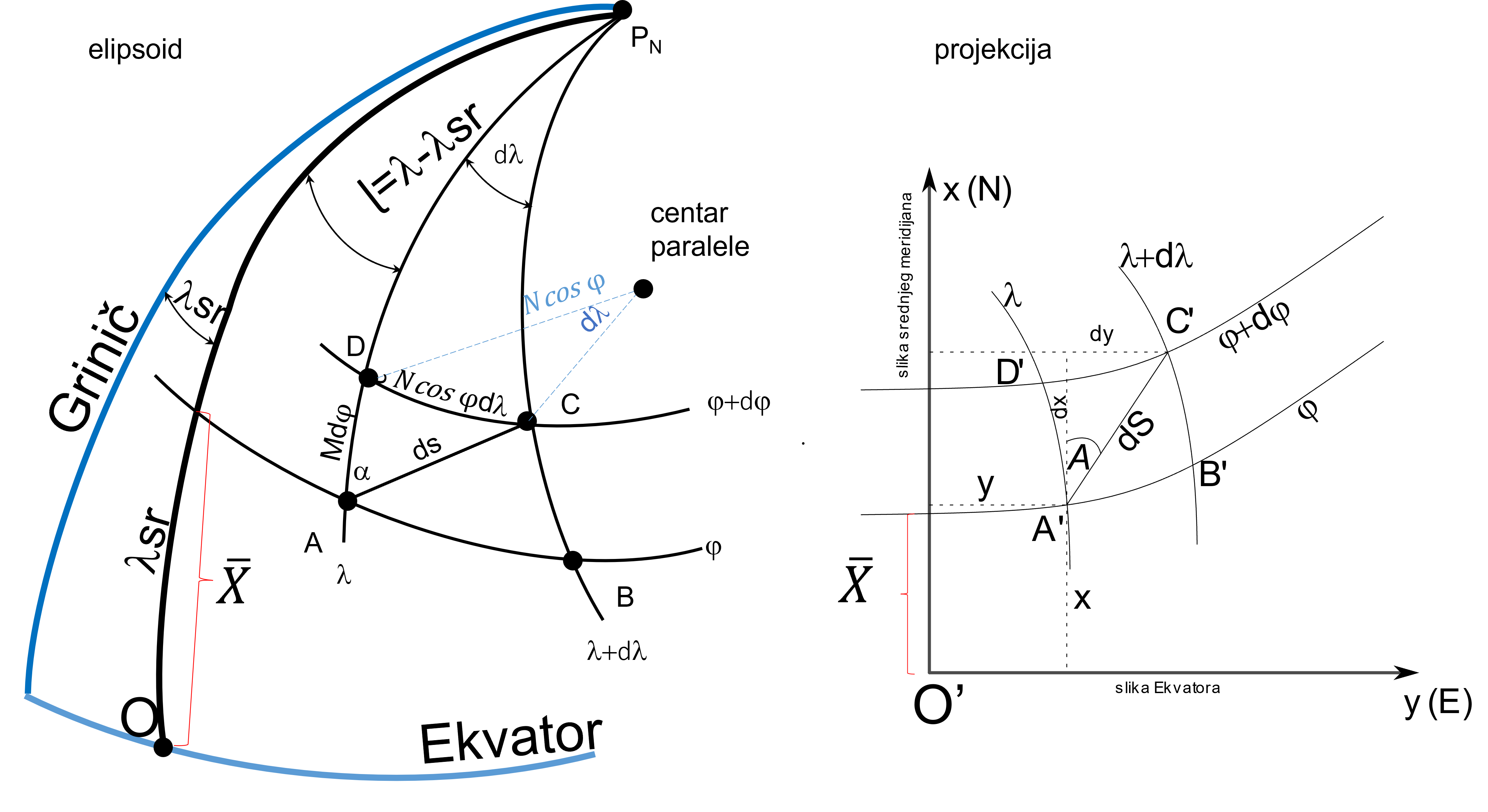
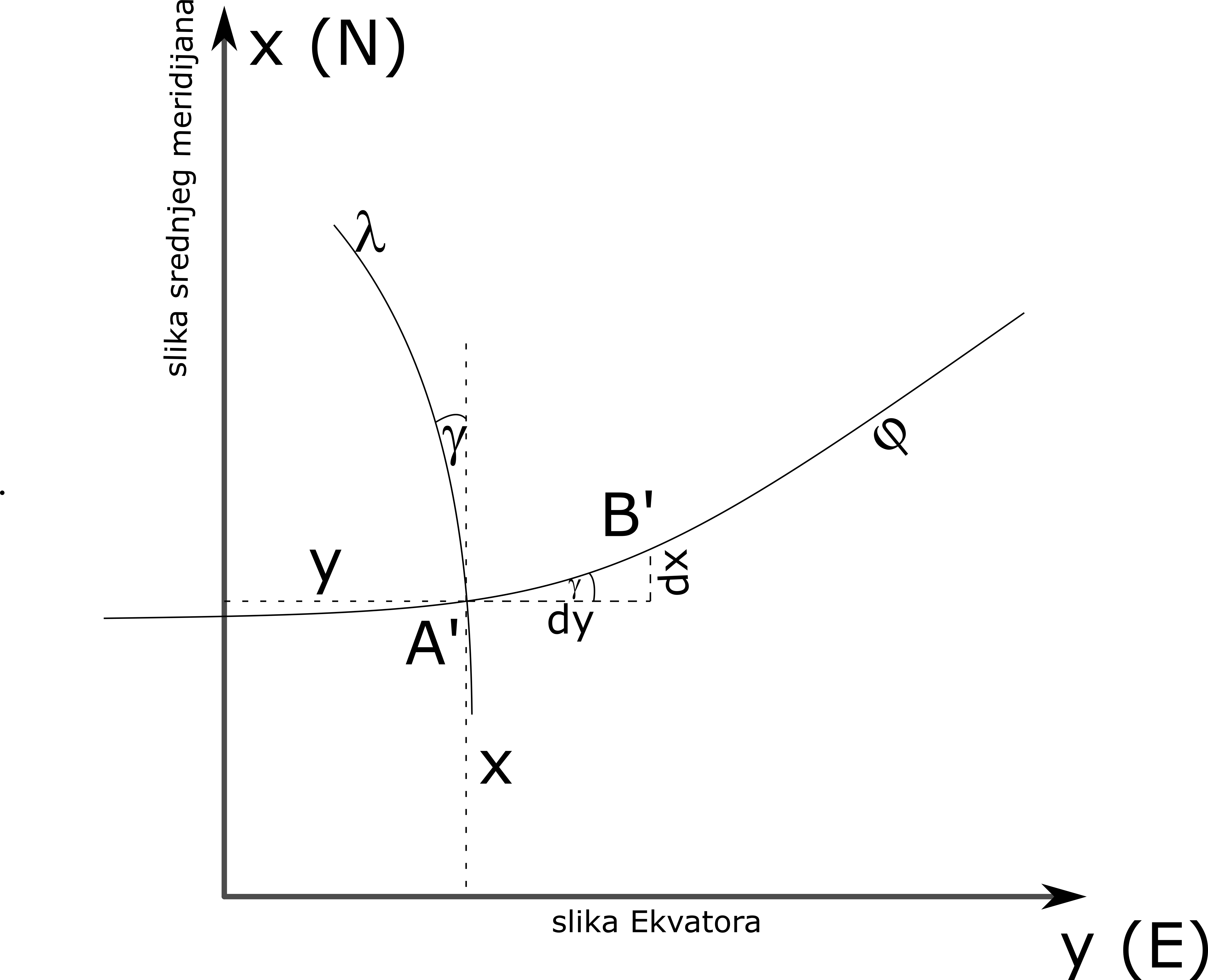
Prvo možemo odrediti linearnu razmeru, uočimo elementarni elipsoidni trapez na elipsoidu i u Gaus-Krigerovoj projekciji, Slika 7.2.

\[ \begin{aligned} c & =\frac{\sqrt{d x^2+d y^2}}{\sqrt{(M d \varphi)^2+(N \cos \varphi d \lambda)^2}}= \\ & =\frac{\sqrt{d x^2+d y^2}}{N \cos \varphi \sqrt{\left(\frac{M d \varphi}{N \cos \varphi}\right)^2+d \lambda^2}} . \end{aligned} \]
Ako sa \(dq\) označimo izraz \(dq=\frac{M d \varphi}{N \cos \varphi}\), imaćemo linearnu razmeru izraženu preko izometrijskih koordinata (izometrijska širina je izvedena i pojašnjena u poglavlju: Cilindrične projekcije 4):
\[ \begin{aligned} & c=\frac{\sqrt{d x^2+d y^2}}{N \cos \varphi \sqrt{d q^2+d \lambda^2}} \\ & c^2=\frac{d x^2+d y^2}{N^2 \cos ^2 \varphi\left(d q^2+d \lambda^2\right)} \end{aligned} \]
Sve konformne projekcije možemo izvesti koristeći kompleksne brojeve i funkcije kompleksnih brojeva gde su koordinate sa elipsoida izražene koristeći izometrijsku širinu.
Kompleksni brojevi su izrazi oblika: \(z = a + bi\), gde su a i b realni brojevi, a \(i\) imaginarni broj koji ima vrednost \(i^2= −1\). Očigledno je da kompleksni broj može se smatrati koordinatama u 2D ravni, i u ovom obliku \(z\) ima koordinate u ravni čije su vrednosti \(a\) i \(b\), Slika 7.3.
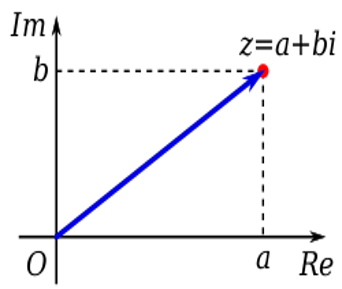
Tako da i linearnu razmeru možemo izraziti koristeći kompleksne brojeve na sledeći način:
\[ \begin{aligned} c^2 & =\frac{d x^2+d y^2}{N^2 \cos ^2 \varphi\left(d q^2+d \lambda^2\right)} =\\ & =\frac{1}{N^2 \cos ^2 \varphi} \frac{(d x+i d y)(d x-i d y)}{(d q+i d \lambda)(d q-i d \lambda)}= \\ & =\frac{1}{N^2 \cos ^2 \varphi} \frac{d(x+i y) d(x-d y)}{d(q+i \lambda) d(q-i \lambda)} \end{aligned} \]
gde je:
\[ i^2=-1 \]
Da bi preslikavanje bilo konformno (linearna razmera je u svim pravcima ista) funkcija za linearnu razmeru \(c\) ne sme zavisiti od azimuta pravca, odnosno ne sme zavisiti od odnosa:
\[ \frac{d y}{d x} \text { ili } \frac{d \lambda}{d \varphi} \mathrm{ili} \frac{d \lambda}{d q^{\prime}} \]
zato što je (fig-eltrgk):
\[ \tan(A)=\frac{d y}{d x} \]
\[ \tan(\alpha)=\frac{N \cos (\varphi) \cdot d \lambda}{M \cdot d \varphi} \]
Funkcija kompleksnog broja ima oblik:
\[ w = f(z)= u + iv \]
\[ w = f(x+iy) = u(x, y) + iv(x, y) \]
gde su \(u\) i \(v\) funkcije realnih brojeva.
Granična vrednost kojom je definisan izvod neke funkcije ne zavisi od načina na koji \(\Delta z\) teži nuli. Kada bi \(f\) bila realna funkcija jedne realne promenljive, onda bi se u definiciji izvoda funkcije \(f\) zahtevalo da \(z\) teži \(z_0\) po realnoj osi, dakle po pravoj. Stoga diferencijabilnost funkcije realne promeljive zahteva manje uslova od diferencijabilnosti funkcije kompleksne promenljive (Kompleksna analiza, Dragan Đorđević, 20.5.2014).
U teoriji kompleksnih brojeva Koši-Rimanova teorema o izvodu kompleksne funkcije glasi: Kompleksna funkcija \(f(z)=u(x,y)+iv(x,y)\) ima kompleksne izvode \(f'(z)\) ako i samo ako njen realni i imaginarni deo su neprekidno diferencijabilni i ako važi: \(u_x=v_y\) i \(u_y=−v_x\) tako da se izvod može zapisati na sledeći način:
\[ f^{\prime}(z)=u_x+iv_x=v_y−iu_y \]
Ovo će biti u slučaju kada su \((x+iy)\) i \((x-iy)\) odgovarajuće funkcije od \((q+iλ\)) i \((q-iλ)\), tj. kada je:
\[ \begin{array}{lll} x+i y=f(q+i \lambda) & \text { i } \quad x-i y=g(q-i \lambda) \\ & \text { ili } \\ x+i y=f(q-i \lambda) & \text { i } \quad x-i y=g(q+i \lambda) \end{array} \]
U skladu sa Koši-Rimanovom teoremom imamo da važi:
\[ \begin{aligned} & d x+i d y=f^{\prime}(q+i \lambda)(d q+i d \lambda) \\ & d x-i d y=g^{\prime}(q-i \lambda)(d q-i d \lambda) \end{aligned} \]
Tako da linearnu razmeru \(c^2 = \frac{1}{N^2 \cos ^2 \varphi} \frac{(d x+i d y)(d x-i d y)}{(d q+i d \lambda)(d q-i d \lambda)}\) možemo izraziti u potpunosti u funkciji izometrijskih koordinata:
\[ c^2=\frac{f^{\prime}(q+i \lambda) g^{\prime}(q-i \lambda)}{N^2 \cos ^2 \varphi} \]
Odavde je očito da je \(c\) funkcija samo od \(q\) i \(\lambda\), a nikako od azimuta pravca čime je uslov konformnosti zadovoljen.
Uslov izražen jednačinama:
\[ \begin{array}{lll} x+i y=f(q+i \lambda) & \text { i } \quad x-i y=g(q-i \lambda) \\ & \text { ili } \\ x+i y=f(q-i \lambda) & \text { i } \quad x-i y=g(q+i \lambda) \end{array} \]
može se primeniti za iznalaženje funkcija traženog konformnog preslikavanja. U teoriji se dokazuje da je za ovu namenu u stvari dovoljna i samo jedna od prethodnih dveju jednačina, na primer, jednačina:
\[ x+i y=f(q+i \lambda) \]
Dakle, prethodnom jednačinom može se definisati bilo koje konformno preslikavanje obrtnog elipsoida na ravan.
Pravougle koordinate
Da bismo dobili jednačine za Gaus-Krigerovu projekciju, oblik funkcije \(f\) treba odrediti imajući u vidu predhono navedene uslove: Kako se srednji meridijan mora preslikati u pravu liniju, koja se usvaja za apscisnu osu x, u jednačini \(x+i y=f(q+i \lambda)\) za \(\lambda = 0\) mora biti i \(y = 0\), dakle:
\[ x = x+i \cdot 0=f(q+i \cdot 0)=f(q) \]
Kako se pored toga i srednji meridijan preslikava bez deformacija to će biti da je vrednost za \(x\) dužina meridijanskog luka na srednjem meridijanu, Slika 7.4:
\[ x+iy = x+i \cdot 0= x = f(q+i \cdot 0)=f(q)=\int_0^\varphi M \cdot d \varphi=L_m=\bar{X} \]
Recimo da svaku funkciju možemo aproksimirati polinomom u okolini nekog broja \(a\); i znamo vrednost funkcije samo u okolini broja \(a\):
\[ f(x)=\sum_{n=0}^{\infty} c_n(x-a)^n=c_0+c_1(x-a)+c_2(x-a)^2+c_3(x-a)^3+c_4(x-a)^4+\cdots \]
Neophodno je da nađemo koeficijente \(c_0, c_1,c_2,c_3 \cdots c_n\) .
U samoj tački \(a\) funkcija ima sledeći oblik:
\[ \begin{aligned} & f(a)=c_0+c_1(a-a)+c_2(a-a)^2+c_3(a-a)^3+c_4(a-a)^4+\cdots \\ & f(a)=c_0 \end{aligned} \]
Ako znamo prvi izvod funkcije možemo odrediti koeficijent \(c_1\):
\[ \begin{array}{cc} f^{\prime}(x) & =c_1+2 c_2(x-a)+3 c_3(x-a)^2+4 c_4(x-a)^3+\cdots \\ f^{\prime}(a) & =c_1 \end{array} \]
Ako znamo 2. izvod funkcije možemo odrediti koeficijent \(c_2\):
\[ \begin{aligned} &\begin{aligned} & f^{\prime \prime}(x)=2 c_2+3(2) c_3(x-a)+4(3) c_4(x-a)^2+\cdots \\ & f^{\prime \prime}(a) \quad=2 c_2 \\ & \end{aligned}\\ &c_2=\frac{f^{\prime \prime}(a)}{2} \end{aligned} \]
Ako znamo 3. izvod funkcije možemo odrediti koeficijent \(c_3\):
\[ \begin{gathered} f^{\prime \prime \prime}(x)=3(2) c_3+4(3)(2) c_4(x-a)+\cdots \\ f^{\prime \prime \prime}(a) \quad=3(2) c_3 \Rightarrow c_3=\frac{f^{\prime \prime \prime}(a)}{3(2)} \end{gathered} \]
U opštem slučaju svaki koeficijent se može sračunati po sledećoj formuli:
\[ c_n=\frac{f^{(n)}(a)}{n !} \]
Tako da funkciju možemo aproksimirati polinomom koji se naziva Tejlorov red:
\[ \begin{gathered} f(x) \quad=\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n !}(x-a)^n \\ =f(a)+f^{\prime}(a)(x-a)+\frac{f^{\prime \prime}(a)}{2 !}(x-a)^2+\frac{f^{\prime \prime \prime}(a)}{3 !}(x-a)^3+\cdots \end{gathered} \] Primer sinusne funkcije u okolini 0: \[ \begin{array}{lll} f^{(0)}(x)=\sin x & f^{(0)}(0)=0 \\ f^{(1)}(x)=\cos x & f^{(1)}(0)=1 \\ f^{(2)}(x)=-\sin x & f^{(2)}(0)=0 \\ f^{(3)}(x)=-\cos x & f^{(3)}(0)=-1 \\ f^{(4)}(x)=\sin x & f^{(4)}(0)=0 \\ f^{(5)}(x)=\cos x & f^{(5)}(0)=1 \\ f^{(6)}(x)=-\sin x & f^{(6)}(0)=0 \end{array} \] \[ \begin{array}{rc} \sin x & =\sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n !} x^n =\frac{1}{1 !} x-\frac{1}{3 !} x^3+\frac{1}{5 !} x^5-\frac{1}{7 !} x^7+\cdots \end{array} \]
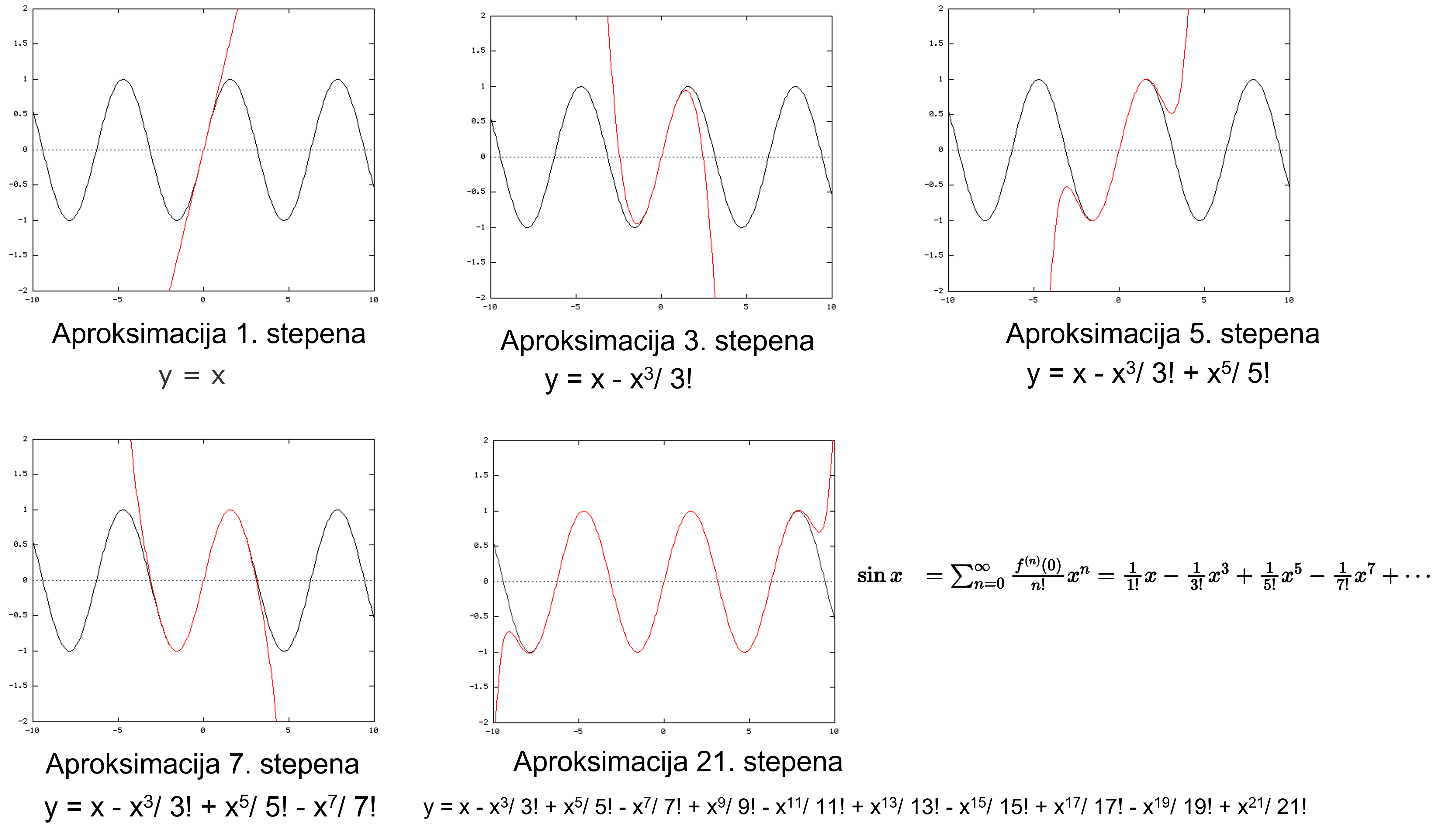
Ako za geografske dužine računate od srednjeg meridijana uvedemo oznaku \(l\) (Slika 7.4, \(l=\lambda- \lambda_{sr}\), redukovana dužina), tada u okolini \(l\) možemo aproksimirati funkciju za preslikavanje elipsoidnih koordinata u pravougle koristeći Tejlorov red (znamo rešenje na srednjem meridijanu kada je \(l=0\) imamo \(x=f(q+i \cdot 0)=f(q)=\int_0^\varphi M \cdot d \varphi=L_m=\bar{X}\)). Zbog tačnosti aproksimacije funkcije usvojimo da širina meridijanskih zona ne bude veća od \(6^o\), odnosno \(│l│ ≤ 3^o\):
\[ \begin{aligned} (x+i y)=f(q)+i l & \frac{d f(q)}{d q}+\frac{(i l)^2}{2} \frac{d^2 f(q)}{d q^2}+\frac{(i l)^3}{6} \frac{d f^3(q)}{d q^3}+ \\ +\frac{(i l)^4}{24} & \frac{d^4 f(q)}{d q^4}+\frac{(i l)^5}{120} \frac{d^5 f(q)}{d g^5}+ \\ & +\frac{(i l)^6}{720} \frac{d^6 f(q)}{d q^6}+\cdots \end{aligned} \]
Imajući u vidu vrednosti za stepene imaginarne jedinice, kao i to da znamo rešenje na srednjem meridijanu kada je \(l=0\):
\[ f(q)=\bar{X} \]
imamo:
\[ \begin{aligned} &(x+i y)= \bar{X}+i l \frac{d \bar{X}}{d q}-\frac{(l)^2}{2} \frac{d^2 \bar{X}}{d q^2}-i \frac{(l)^3}{6} \frac{d \bar{X}}{d q^3}+ \\ &-\frac{(l)^4}{24} \frac{d^4 \bar{X}}{d q^4}-i \frac{(l)^5}{120} \frac{d^5 \bar{X}}{d g^5}+ \\ &-\frac{(l)^6}{720} \frac{d^6 \bar{X}}{d q^6}+\cdots \end{aligned} \] Ako se izdvoje posebno realni i posebno imaginarni članovi imaćemo:
\[ \begin{gathered} x=\bar{X}-\frac{l^2}{2} \frac{d^2 \bar{X}}{d q^2}+\frac{l^4}{24} \frac{d^4 \bar{X}}{d q^4}-\frac{l^6}{720} \frac{d^6 \bar{X}}{d q^6}+\cdots \\ y=l \frac{d \bar{X}}{d q}-\frac{l^3}{6} \frac{d^3 \bar{X}}{d q^3}+\frac{l^5}{120} \frac{d^5 \bar{X}}{d q^5}-\cdots \end{gathered} \]
Za definitivan oblik prethodnih funkcija treba odrediti izvode:
\[ \frac{d^n \bar{X}}{d q^n} \]
\[ n=1,2,3 \ldots \]
Imajući u vidu traženu tačnost u triangulaciji kao i to da je \(│l│ ≤ 3^o\) potrebno je odrediti pomenute izvode do 6. reda. Ove izvode sračunaćemo imajući u vidu sledeće diferencijalne odnose složenih funkcija:
\[ \frac{d \bar{X}}{d q}=\frac{d \bar{X}}{d \varphi} \frac{d \varphi}{d q} \]
\[ \frac{d^2 \bar{X}}{d q^2}=\frac{d}{d \varphi}\left(\frac{d \bar{X}}{d q}\right) \frac{d \varphi}{d q} \]
\[ \frac{d^3 \bar{X}}{d q^3}=\frac{d}{d \varphi}\left(\frac{d^2 \bar{X}}{d q}\right) \frac{d \varphi}{d q} \quad \dots \] Kako je diferencijalni meridijanski luk jednak:
\[ d \bar{X}= dL_m= M \cdot d \varphi \quad \Rightarrow \quad \frac{d \bar{X}}{d \varphi}=M \]
i kako je (ovo smo radili kod konformne širine):
\[ d q=\frac{M \cdot d \varphi}{N \cos \varphi} \quad \Rightarrow \quad \frac{d \varphi}{d q} = \frac{Ncos \varphi}{ M } \]
Za prvi izvod dobijamo \(\frac{d \bar{X}}{d q}=\frac{d \bar{X}}{d \varphi} \frac{d \varphi}{d q}\):
\[ \frac{d \bar{X}}{d q} = \frac{d \bar{X}}{d \varphi} \frac{d \varphi}{d q} =M \frac{N \cos \varphi}{M}=N \cos \varphi \] Dalje će drugi izvod biti:
\[ \frac{d^2 \bar{X}}{d q^2}=\frac{d}{d \varphi}\left(\frac{d \bar{X}}{d q}\right) \frac{d \varphi}{d q} =\left[\frac{d}{d \varphi}(N \cos \varphi)\right] \frac{N \cos \varphi}{M} \] Podsetimo se izraza za N i M:
\[ N=\frac{a}{\sqrt{1-e^2 \sin ^2 \varphi}} \]
\[ M=M(\varphi)=\frac{(a b)^2}{\left((a \cdot \cos \varphi)^2+(b \cdot \sin \varphi)^2\right)^{\frac{3}{2}}}=\frac{a\left(1-e^2\right)}{\left(1-e^2 \sin ^2 \varphi\right)^{\frac{3}{2}}} \]
\[ e^2=1-\frac{b^2}{a^2} \]
Da bismo našli izvod \(\frac{d N}{d \varphi}\), uvodimo smenu \(u=e sin \varphi\), tada je \(\frac{d u}{d \varphi} = e cos \varphi\), N u funkciji od \(u\) je \(N=\frac{a}{\sqrt{1-u^2}} = a (1-u^2)^{-1/2}\) imamo da je:
\[ \frac{d N}{d u} = a \cdot (-1/2)\cdot (1 - u^2)^{-3/2} \cdot 2u \]
Vratimo smenu nazad, tada imamo:
\[ \frac{d N}{d( e sin \varphi)} = \frac{d N}{d u} \frac{d u}{d \varphi} \]
\[ \frac{d N}{d( e sin \varphi)} = a \cdot (-1/2) \cdot (1 - (e \cdot sin\varphi)^2)^{-3/2}\cdot 2(e \cdot sin(\varphi)) \cdot e \cdot cos(\varphi) \]
Dalje je \(\frac{d N}{d \varphi}\):
\[ \frac{d N}{d \varphi} = \frac{d N}{d( e sin \varphi)} \frac{d( e sin \varphi)}{d \varphi} \]
\[ \frac{d N}{d \varphi} = -a \cdot e^2 \cdot cos(\varphi) \cdot (1 - e^2 \cdot sin^2(\varphi))^{-3/2} \cdot e \cdot cos(\varphi) \]
Kada se sredi izraz dobija se:
\[ \frac{d N}{d \varphi} = -a \cdot e^2 cos^2(\varphi) (1 - e^2 \cdot sin^2(\varphi))^{-3/2} \]
Dalje bi prethodni izraz mogao da se sređuje i svede na jednačinu oblika:
\[ \frac{dN}{d \varphi}=(N-M) \tan \varphi \]
Tako da je rešenje za drugi izvod:
\[ \begin{gathered} \frac{d^2 \bar{X}}{d q^2}=\frac{d}{d \varphi}\left(\frac{d \bar{X}}{d q}\right) \frac{d \varphi}{d q}=\left[\frac{d}{d \varphi}(N \cos \varphi)\right] \frac{N \cos \varphi}{M}= \\ =\left[\frac{d N}{d \varphi} \cos \varphi-N \sin \varphi\right] \frac{N \cos \varphi}{M}= \\ =[((N-M) \tan \varphi) \cos \varphi-N \sin \varphi] \frac{N \cos \varphi}{M}= \\ =-M \sin \varphi \frac{N \cos \varphi}{M}=-N \sin \varphi \cos \varphi \end{gathered} \]
Dalje ćemo za treći izvod dobiti:
\[ \begin{gathered} \frac{d^3 \bar{X}}{d q^3}=\left[\frac{d}{d \varphi}(-N \sin \varphi \cos \varphi)\right] \frac{N \cos \varphi}{M}= \\ =\left[\frac{d(-N \cos \varphi)}{d \varphi} \sin \varphi-N \cos \varphi \frac{d}{d \varphi} \sin \varphi\right] \frac{N \cos \varphi}{M}= \\ =\left(M \sin ^2 \varphi-N \cos ^2 \varphi\right) \frac{N \cos \varphi}{M}= \\ =N \sin ^2 \varphi \cos \varphi-\frac{N^2}{M} \cos ^2 \varphi= \\ =-N \cos ^3 \varphi\left(\frac{N}{M}-\frac{\sin ^2 \varphi}{\cos ^2 \varphi}\right)=-N \cos ^3 \varphi\left(\frac{N}{M}-\operatorname{tan}^2 \varphi\right) . \end{gathered} \]
Možemo dalje uočiti odnos između N i M:
\[ \begin{gathered} \frac{N}{M}=\frac{1-e^2 \sin ^2 \varphi}{1-e^2}= \\ =\frac{1-e^2+e^2 \cos ^2 \varphi}{1-e^2}= \\ =1+\frac{e^2}{1-e^2} \cos ^2 \varphi= \\ =1+e^{\prime 2} \cos ^2 \varphi \end{gathered} \]
\[ e^{\prime 2}=\frac{a^2-b^2}{b^2} \]
i ako uvedemo oznake:
\[ \begin{gathered} \tan \varphi=t \\ e^{\prime} \cos \varphi=\eta \end{gathered} \]
Dobijamo onda:
\[ \frac{d^3 \bar{X}}{d q^3}=-N \cos ^3 \varphi\left(1-t^2+\eta^2\right) \] Sličnim postupkom računaju se i ostali izvodi, pa ćemo navesti njihove definitivne formule:
\[ \frac{d^4 \bar{X}}{d q^4}=N \sin \varphi \cos ^3 \varphi\left(5-t^2+9 \eta^2+4 \eta^4\right) \]
\[ \frac{d^5 \bar{X}}{d q^5}=N \cos ^5 \varphi\left(5+14 \eta^2-18 t^2-58 \eta^2 t^2+t^4\right) \]
\[ \frac{d^6 \bar{X}}{d q^6}=-N \cos ^5 \varphi \sin \varphi\left(61+270 \eta^2-58 t^2+t^4-330 t^2 n^2\right) \]
Pošto dobijene izvode uvrstimo u prethodne funkcije za \(x\) i \(y\) dobijamo njihove definitivne Gausove jednačine kada su zadate geografske koordinate (\(\varphi\), \(\lambda\)), napomena \(l\) je redukovana širina \(l=\lambda - \lambda_{sr}\) izražena u radijanima:
\[ \begin{aligned} x= & \bar{X}+\frac{l^2}{2} N \sin \varphi \cos \varphi+\frac{l^4}{24} N \sin \varphi \cos ^3 \varphi\left(5-t^2+9 \eta^2+4 \eta^4\right)+ \\ & +\frac{l^6}{720} N \sin \varphi \cos ^5 \varphi\left(61-58 t^2+t^4\right) \\ y= & l N \cos \varphi+\frac{l^3}{6} N \cos ^3 \varphi\left(1+\eta^2-t^2\right)+ \\ & +\frac{l^5}{120} N \cos ^5 \varphi\left(5-18 t^2+t^4+14 \eta^2-58 \eta^2 t^2\right) \end{aligned} \]
Ako je \(l\) u stepenima, formule će glasiti:
\[ \begin{aligned} x= & \bar{X}+\frac{l^2}{2 \rho^2} N \sin \varphi \cos \varphi+\frac{z l^4}{24 \rho^4} N \sin \varphi \cos ^3 \varphi\left(5-t^2+9 \eta^2+4 \eta^4\right)+ \\ & +\frac{l^6}{720 \rho^6} N \sin \varphi \cos ^5 \varphi\left(61-58 t^2+t^4\right) \\ y= &\frac{l}{\rho} N \cos \varphi+\frac{l^3}{6 \rho^3} N \cos ^3 \varphi\left(1+\eta^2-t^2\right)+ \\ & +\frac{l^5}{120 \rho^5} N \cos ^5 \varphi\left(5-18 t^2+t^4+14 \eta^2-58 \eta^2 t^2\right) \end{aligned} \]
Gde je:
\[ \rho=\frac{180}{\pi} \]
Ako se dalje uvedu uobičajene oznake, možemo definisati konačne grupisane formule za direktni zadatak:
\[ \begin{aligned} x= & x(\varphi, \lambda)=\bar{X}(\varphi)+A_2(\varphi) \cdot l^2+A_4(\varphi) \cdot l^4+A_6(\varphi) \cdot l^6 \\ y= &y(\varphi, \lambda)=A_1(\varphi) \cdot l+A_3(\varphi) \cdot l^3+A_5(\varphi) \cdot l^5 \end{aligned} \]
Formulu za dužinu meridijanskog luka smo definisali ranije (dobro je napisati ponovo uz grupisane formule):
\[ \begin{aligned} &\bar{X}(\varphi)=a \cdot\left(1-e^2\right) \cdot\left(A \cdot \varphi-\frac{B}{2} \cdot \sin (2 \cdot \varphi)+\frac{C}{4} \cdot \sin (4 \cdot \varphi)-\frac{D}{6} \cdot \sin (6 \cdot \varphi)\right) \\ & A=1+\frac{3}{4} e^2+\frac{45}{64} e^4+\frac{175}{256} e^6+\ldots \\ & B=\frac{3}{4} e^2+\frac{15}{16} e^4+\frac{525}{512} e^6+\ldots \\ & C=\quad \frac{15}{64} e^4+\frac{105}{256} e^6+\ldots \\ & D=\quad \frac{35}{256} e^6+\ldots \end{aligned} \]
\[ l=\lambda-\lambda s r \]
\[ t(\varphi)=\operatorname{tan}(\varphi) \] \[ \eta(\varphi)=e_1 \cdot \cos (\varphi) \] \[ e_1^2 = e^{\prime 2}= \frac{a^2-b^2}{b^2} \]
\[ N=\frac{a}{\sqrt{\left(1-e^2 \sin (\varphi)^2\right)}} \] \[ e^2=1-\frac{b^2}{a^2} \]
\[ \begin{aligned} &A_1=N(\varphi) \cdot \cos (\varphi) \\ & A_2=N(\varphi) \cdot \sin (\varphi) \cdot \frac{\cos (\varphi)}{2} \\ & A_3=N(\varphi) \cdot \cos (\varphi)^3 \cdot \frac{1+\eta(\varphi)^2-t(\varphi)^2}{6}\\ & A_4=N(\varphi) \cdot \sin (\varphi) \cdot \cos (\varphi)^3 \cdot \frac{5-t(\varphi)^2+9 \cdot \eta(\varphi)^2+4 \cdot \eta(\varphi)^4}{24} \\ & A_5=N(\varphi) \cdot \cos (\varphi)^5 \cdot \frac{5-18 \cdot t(\varphi)^2+t(\varphi)^4+14 \cdot \eta(\varphi)^2-58 \cdot \eta(\varphi)^2 \cdot t(\varphi)^2}{120} \\ & A_6=N(\varphi) \cdot \sin (\varphi) \cdot \cos (\varphi)^5 \cdot \frac{61-58 \cdot t(\varphi)^2+t(\varphi)^4}{720} \end{aligned} \]
Razmera površina
Pođimo od poznate jednačine linearne razmere:
\[ c^2=\frac{d x^2+d y^2}{N^2 \cos ^2 \varphi\left(d q^2+d l^2\right)} \]
Kako je reč o konformnoj projekciji, razmatranje možemo pojednostaviti ako potražimo formulu za linernu razmeru u pravcu paralele \(n\). Kako je duž paralele je \(d \varphi=0\), to će totalni diferencijali \(dx\) i \(dy\) biti:
\[ d x=\frac{\partial x}{\partial l} d l \]
\[ d y=\frac{\partial y}{\partial l} d l \]
pa će dalje važiti:
\[ c=m=n=\frac{\sqrt{\left(\frac{\partial x}{\partial l}\right)^2+\left(\frac{\partial y}{\partial l}\right)^2}}{N \cos \varphi} \]
Možemo odrediti izraze za \(\frac{\partial x}{\partial l}\) i \(\frac{\partial y}{\partial l}\):
\[ \begin{aligned} x= & \bar{X}+\frac{l^2}{2} N \sin \varphi \cos \varphi+\frac{l^4}{24} N \sin \varphi \cos ^3 \varphi\left(5-t^2+9 \eta^2+4 \eta^4\right)+ \\ & +\frac{l^6}{720} N \sin \varphi \cos ^5 \varphi\left(61-58 t^2+t^4\right) \\ y= & l N \cos \varphi+\frac{l^3}{6} N \cos ^3 \varphi\left(1+\eta^2-t^2\right)+ \\ & +\frac{l^5}{120} N \cos ^5 \varphi\left(5-18 t^2+t^4+14 \eta^2-58 \eta^2 t^2\right) \end{aligned} \]
Ako tražimo izvod po \(l\), imamo:
\[ \frac{\partial x}{\partial l}=\frac{2 l}{2} N \sin \varphi \cos \varphi+\frac{4 l^3}{24} N \sin \varphi \cos ^3 \varphi\left(5-t^2+9 \eta^2+4 \eta^4\right)+\cdots \]
\[ \frac{\partial y}{\partial l}=N \cos \varphi+\frac{3 l^2}{6} N \cos ^3 \varphi\left(1+\eta^2-t^2\right)+\cdots \]
Ako izvršimo njihovo kvadriranje i pri tome odbacimo članove \(\eta^2, t^4, \dots\) i uzmemo samo prva dva člana, imamo:
\[ \left(l N \sin \varphi \cos \varphi+\frac{4 l^3}{24} N \sin \varphi \cos ^3 \varphi\left(5-t^2+9 \eta^2+4 \eta^4\right)\right)^2=(a+b)^2=a^2+2 a b+b^2 \]
\[ \left(\frac{\partial x}{\partial l}\right)^2=l^2 N^2 \sin ^2 \varphi \cos ^2 \varphi+\frac{l^4}{3} N^2 \sin ^2 \varphi \cos ^4 \varphi\left(5-t^2\right) \]
\[ \left(\frac{\partial y}{\partial l}\right)^2=N^2 \cos ^2 \varphi+l^2 N^2 \cos ^4 \varphi\left(1-t^2+\eta^2\right)+\frac{l^4}{12} N^2 \cos ^6 \varphi\left(8-24 t^2\right) \]
Potom podelimo sve sa \(N^2cos^2\varphi\) da bismo dobili razmeru površina, jer je kod konformnih projekcija \(p = c^2\):
\[ p=1+l^2 \cos ^2 \varphi\left(1+\eta^2\right)+\frac{l^4}{3} \cos ^4 \varphi\left(2-t^2\right) \]
Odnosno, ako su \(l\) i \(\varphi\) u stepenima konvertujemo u radijane deljenjem uglova sa \(\rho=\frac{180}{\pi}\):
\[ p=1+\frac{l^2}{\rho^2} \cos ^2 \varphi\left(1+\eta^2\right)+\frac{l^4}{3 \rho^4} \cos ^4 \varphi\left(2-t^2\right) \]
Linearna razmera
Izraz za linearnu razmeru dobija se stepenovanjem prethodnog izraza za razmeru površina \(p=1+l^2 \cos ^2 \varphi\left(1+\eta^2\right)+\frac{l^4}{3} \cos ^4 \varphi\left(2-t^2\right)\) eksponentom 1/2 koristeći formulu za razvijanje u red funkcije (1+x)1/2:
Treba naći Tejlorov red za aproksimaciju funkcije \(y = (1+x)^{\frac{1}{2}}\) u okolini tačke \(x = 0\): Izvodi funkcije:
\[ \begin{aligned} y &= (1+x)^{\frac{1}{2}} \\ y' &= \frac{d}{dx}[(1+x)^{\frac{1}{2}}] = \frac{1}{2}(1+x)^{-\frac{1}{2}} = \frac{1}{2\sqrt{1+x}} \\ y'' &= \frac{d^2}{dx^2}[(1+x)^{\frac{1}{2}}] = \frac{d}{dx}\left[\frac{1}{2\sqrt{1+x}}\right] = -\frac{1}{4}(1+x)^{-\frac{3}{2}} = -\frac{1}{4(1+x)^{\frac{3}{2}}} \\ y''' &= \frac{d^3}{dx^3}[(1+x)^{\frac{1}{2}}] = \frac{d}{dx}\left[-\frac{1}{4(1+x)^{\frac{3}{2}}}\right] = \frac{3}{8}(1+x)^{-\frac{5}{2}} = \frac{3}{8(1+x)^{\frac{5}{2}}} \end{aligned} \] Vrednosti u okolini \(x = 0\):
\[ \begin{aligned} y(0) &= (1+0)^{\frac{1}{2}} = 1 \\ y'(0) &= \frac{1}{2\sqrt{1+0}} = \frac{1}{2} \\ y''(0) &= -\frac{1}{4(1+0)^{\frac{3}{2}}} = -\frac{1}{4} \\ y'''(0) &= \frac{3}{8(1+0)^{\frac{5}{2}}} = \frac{3}{8} \end{aligned} \]
Tejlorov red ima oblik:
\[ y(x) = (1+x)^{\frac{1}{2}} = y(0) + y'(0)x + \frac{y''(0)}{2!}x^2 + \frac{y'''(0)}{3!}x^3 + \cdots \]
Zamenom sračunatih vrednosti dobijamo konačan oblik u okolini \(x = 0\):
\[ y(x) = (1+x)^{\frac{1}{2}} = 1 + \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16}x^3 + \cdots \]
Pošto je \(p\):
\[ p=1+l^2 \cos ^2 \varphi\left(1+\eta^2\right)+\frac{l^4}{3} \cos ^4 \varphi\left(2-t^2\right) \] Ako uvedemo smenu \(u = l^2 \cos ^2 \varphi\left(1+\eta^2\right)+\frac{l^4}{3} \cos ^4 \varphi\left(2-t^2\right)\) onda je \(p=1+u\), tako da možemo naći \(c=m=n=\sqrt{p}=(1+u)^{\frac{1}{2}}\) koristeći Tejlorov red:
\[ c=m=n=\sqrt{p}=(1+u)^{\frac{1}{2}}= 1 + \frac{1}{2}u - \frac{1}{8}u^2 + \frac{1}{16}x^3 + \cdots \]
Vratimo vrednost za \(u\) i imamo:
\[ c= 1 + \frac{l^2 \cos^2 \varphi (1 + \eta^2) + \frac{l^4}{3} \cos^4 \varphi (2 - t^2)}{2} - \frac{\left(l^2 \cos^2 \varphi (1 + \eta^2) + \frac{l^4}{3} \cos^4 \varphi (2 - t^2)\right)^2}{8} + \cdots \]
U literaturi se uglavnom još više uprošćava polimon koji predstavlja funkciju za računanje linearne razmere u obliku:
\[ c= 1 + \frac{l^2 \cos^2 \varphi (1 + \eta^2) + \frac{l^4}{3} \cos^4 \varphi (2 - t^2)}{2} - \frac{\left(l^2 \cos^2 \varphi (1 + \eta^2) + \frac{l^4}{3} \cos^4 \varphi (2 - t^2)\right)^2}{8} + \cdots \]
Treba napomenuti da se gornji izraz sad može koristiti bez daljeg uprošćavanja, s obzirom na računarske mogućnosti. Nakon sređivanja izraza i zanemarivanja članova većeg stepena od \(l^4, l^6, \eta^2\) dobija se:
\[ c=1+\frac{l^2}{2} \cos ^2 \varphi\left(1+\eta^2\right)+\frac{l^4}{24} \cos ^4 \varphi\left(5-4 t^2\right) \]
Ako su uglovi u stepenima konvertujemo u radijane deljenjem uglova sa \(\rho=\frac{180}{\pi}\):
\[ c=1+\frac{l^2}{2 \rho^2} \cos ^2 \varphi\left(1+\eta^2\right)+\frac{l^4}{24 \rho^4} \cos ^4 \varphi\left(5-4 t^2\right) \]
Ili konačno uvođenjem koeficijenata (koji zavise samo od \(\varphi\), gde su uglovi izraženi u stepenima):
\[ \begin{aligned} C_1 & =\frac{\cos ^2 \varphi}{2 \rho^2}\left(1+\eta^2\right) \\ C_2 & =\frac{\cos ^4 \varphi}{24 \rho^4}\left(5-4 t^2\right)\\ c& =1+C_1 l^2+C_2 l^4 \end{aligned} \]
- Kod izvorne Gaus-Krigerove projekcije uvek je \(c ≥ 1\), dakle, preslikane dužine su veće nego na površi elipsoida,
- Iako je linearna razmera funkcija od \(\varphi\) i od \(l\) (odnosno \(\lambda\)), na njenu promenu mnogo više utiče promena geodetske dužine nego geodetske širine, jer se \(cos \varphi\) menja sporije i u mnogo užim granicama (od 0 do 1).
- Najveću vrednost funcije \(c\) i \(p\) imaju na presečnim tačkama meridijanskih zona preslikavanja, a na polovima imaju vrednost 1.
- Na srednjem meridijanu, gde je \(l = 0\), \(c=1\) i \(p=1\), prema za unapred zadatim uslovima za projekciju.
Konvergencija meridijana
KONVERGENCIJA MERIDIJANA (\(\gamma\)) je ugao koji u zadatoj tački u projekciji zaklapa tangenta na slici meridijana sa pravom paralelnom \(x\) osi (mereno u pravcu kretanja kazaljke na satu). Tačke istočno od srednjeg meridijana imaju pozitivnu konvergenciju meridijana, dok tačke zapadno od srednjeg meridijana imaju negativnu konvergenciju meridijana, Slika 7.6.
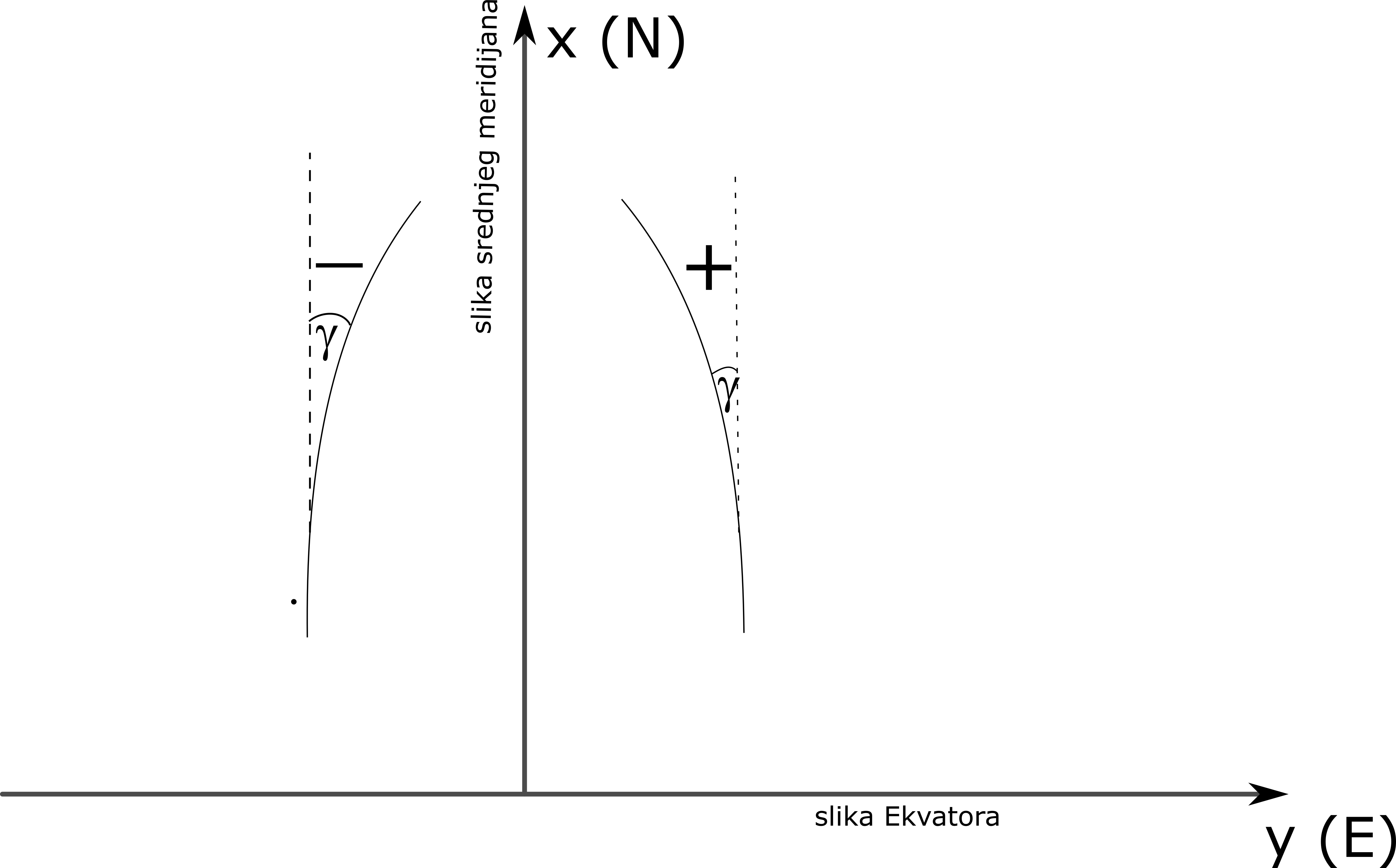
Značaj: Pomoću konvergencije meridijana (\(\gamma\)) na osnovu azimuta geodetske linije na elipsoidu (\(\alpha\)) moguće je odrediti geodetski (Gausov) direkcioni ugao (A) (nagib) linije u projekciji, Slika 7.7.
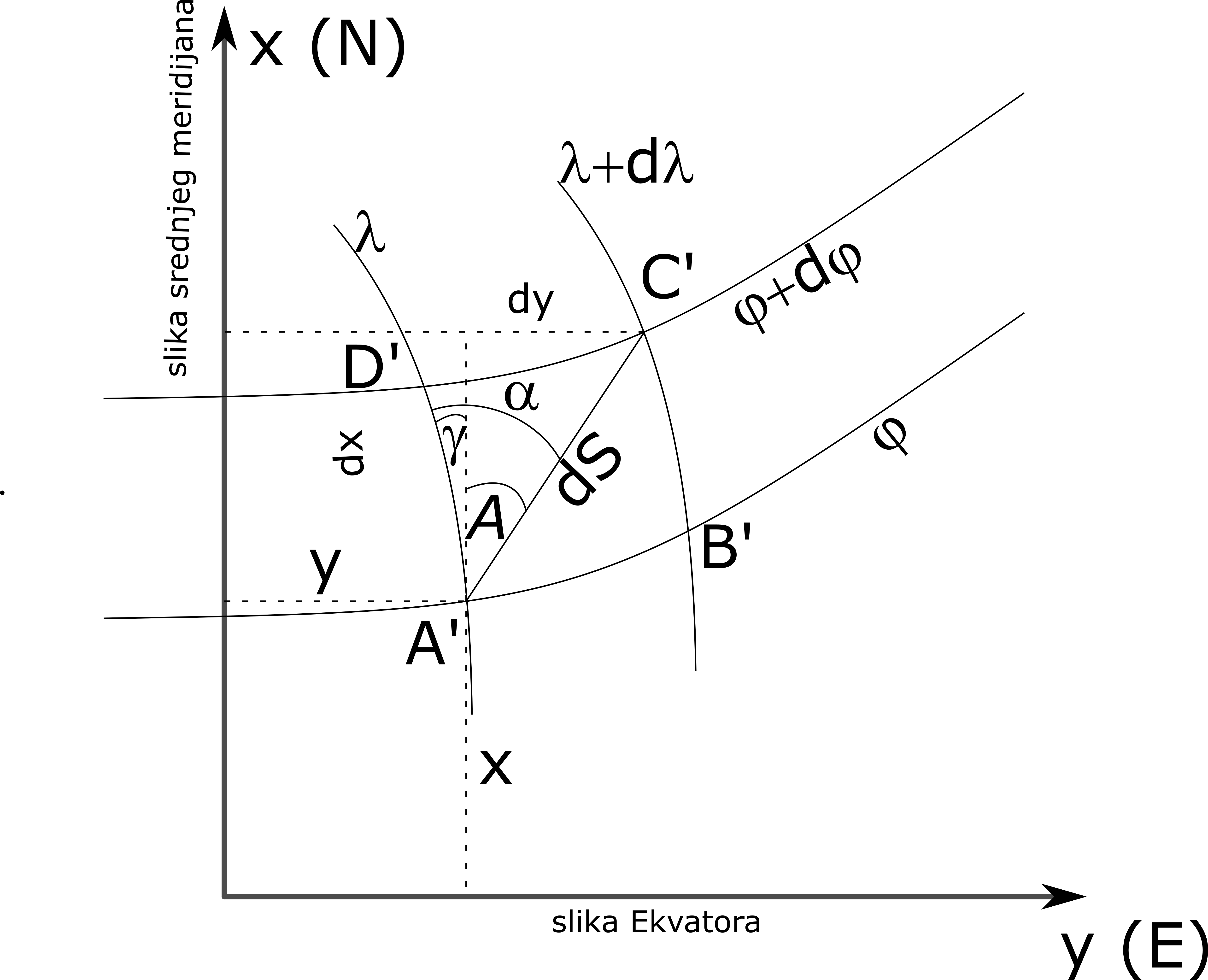
Kako je ugao između meridijana i paralele u projekciji prav, to je, Slika 7.8:
\[ \operatorname{tan} \gamma=\frac{d x}{d y} \]
Kako se tačka \(B’\) po pretpostavci nalazi na slici paralele, pa je \(d\varphi = 0\), zato će važiti:
\[ d x=\frac{\partial x}{\partial l} d l \quad \text { odnosno, } \quad d y=\frac{\partial y}{\partial l} d l \]
\[ \operatorname{tan} \gamma=\frac{\frac{\partial x}{\partial l}}{\frac{\partial y}{\partial l}} \]
Potrebni parcijalni izvodi u imeniocu i brojiocu mogu se odrediti na osnovu ranije izvedenih formula za računanje pravouglih koordinata na osnovu geografskih, te će biti:
\[ \frac{\partial x}{\partial l}=\frac{2 l}{2} N \sin \varphi \cos \varphi+\frac{4 l^3}{24} N \sin \varphi \cos ^3 \varphi\left(5-t^2+9 \eta^2+4 \eta^4\right)+\cdots \]
\[ \frac{\partial y}{\partial l}=N \cos \varphi+\frac{3 l^2}{6} N \cos ^3 \varphi\left(1+\eta^2-t^2\right)+\cdots \]
U daljem izvođenju najpre se oba prethodna izraza podele sa \(N\cos \varphi\), razlomak za računanje tangensa se neće promeniti:
\[ \begin{array}{r} \frac{\partial x}{\partial l} \frac{1}{N \cos \varphi}&=l \sin \varphi+\frac{l^3}{6} \sin \varphi \cos ^2 \varphi\left(5-t^2+9 \eta^2\right)+\frac{l^5}{120} \sin \varphi \cos ^4 \varphi\left(61-58 t^2+t^4\right) \\ \frac{\partial y}{\partial l} \frac{1}{N \cos \varphi}&=1+\frac{l^2}{2} \cos ^2 \varphi\left(1-t^2+\eta^2\right)+\frac{l^4}{24} \cos ^4 \varphi\left(5-18 t^2+t^4\right) \end{array} \]
Zatim se nađe recipročna vrednost drugog izraza na osnovu formule za razvijanje u red funkcije \((1+x)^{-1}\)
\[ (1+x)^{-1}=1-x+x^2-x^3+x^4-x^5 \ldots \]
\[ \frac{\partial y}{\partial l} \frac{1}{N \cos \varphi}=1+\frac{l^2}{2} \cos ^2 \varphi\left(1-t^2+\eta^2\right)+\frac{l^4}{24} \cos ^4 \varphi\left(5-18 t^2+t^4\right) \]
\[ \begin{aligned} & \frac{N \cos \varphi}{\frac{\partial y}{\partial l}}=1-\frac{l^2}{2} \cos ^2 \varphi\left(1-t^2+\eta^2\right)-\frac{l^4}{24} \cos ^4 \varphi\left(5-18 t^2+t^4\right)+\frac{l^4}{4} \cos ^4 \varphi\left(1-2 t^2+t^4\right)+\cdots \\ & =1-\frac{l^2}{2} \cos ^2 \varphi\left(1-t^2+\eta^2\right)+\frac{l^4}{24} \cos ^4 \varphi\left(1+6 t^2+5 t^4\right) \end{aligned} \]
Računanje konvergencije meridijana u ravni na osnovu geodetskih koordinata \(\varphi, l\), (napomena \(l=\lambda-\lambda_{sr}\)) :
\[ \begin{aligned} & \operatorname{tan} \gamma &=l \sin \varphi+\frac{l^3}{3} \sin \varphi \cos ^2 \varphi\left(1+t^2+3 \eta^2\right)+\frac{l^5}{16} \sin \varphi \cos ^4 \varphi\left(2+4 t^2+2 t^4\right) \\ & \gamma &=\operatorname{atan}\left(l \sin \varphi+\frac{l^3}{3} \sin \varphi \cos ^2 \varphi\left(1+t^2+3 \eta^2\right)+\frac{l^5}{16} \sin \varphi \cos ^4 \varphi\left(2+4 t^2+2 t^4\right)\right) \end{aligned} \]
7.2 Inverzno preslikavanje
Rešenje obrnutog zadatka matematičke kartografije podrazumeva iznalaženje formula za inverzno preslikavanje sa projekcione ravni na obrtni elipsoid, kao i odgovarajućih formula za prateće deformacione karakteristike . Dakle, ako su nam poznate pravougle koordinate tačke u ravni \((x,y)\), treba odrediti formule za računanje geodetskih koordinata odgovarajuće tačke na obrtnom elipsoidu \((\varphi, \lambda)\). Ovde će se zadatak rešiti korišćenjem izometrijskih koordinata na \((q,l)\) na obrtnom elipsoidu.
Opšte jednačine inverznog preslikavanja u izometrijskim koordinatama glase:
\[ \begin{aligned} & q=F_1(x, y) \\ & l=F_2(x, y) \end{aligned} \]
Posle određivanja koordinata \((q,l)\) prelazak iz izometrijskih na geografske koordinate obaviće se na osnovu prethodno već poznatih relacija. Poznato je da se konformno preslikavanje sa ravni na obrtni elipsoid može izraziti kao:
\[ q+i l=f(x+i y) \]
Kod Gaus-Krigerove projekcije, na osnovu prethodno postavljenog uslova imamo da važi: za \(y = 0\), biće i \(l = 0\), te će duž x ose (slike srednjeg meridijana) važiti:
\[ q=f(x) \]
Na osnovu uslova da duž srednjeg meridijana nema linearnih deformacija, odnosno da važi da je \(c = 1\), to će za duž srednjeg meridijana važiti:
\[ x=f(q)=\int_0^\phi M \cdot d \phi=\bar{X} \]
No, ako proizvoljnoj tački sa koordinatama \((x, y)\), gde je \(y \neq 0\), odgovaraju koordinate \((q, l)\) to duž srednjeg meridijana apscisi \(x\) neće odgovarati izometrijska širina \(q\) već neka širina \(q1\) odnosno neka geografska širina \(\varphi_1\). Stoga će duž srednjeg meridijana važiti, Slika 7.9:
\[ q_1=f(x)=f(\bar{X}) \]
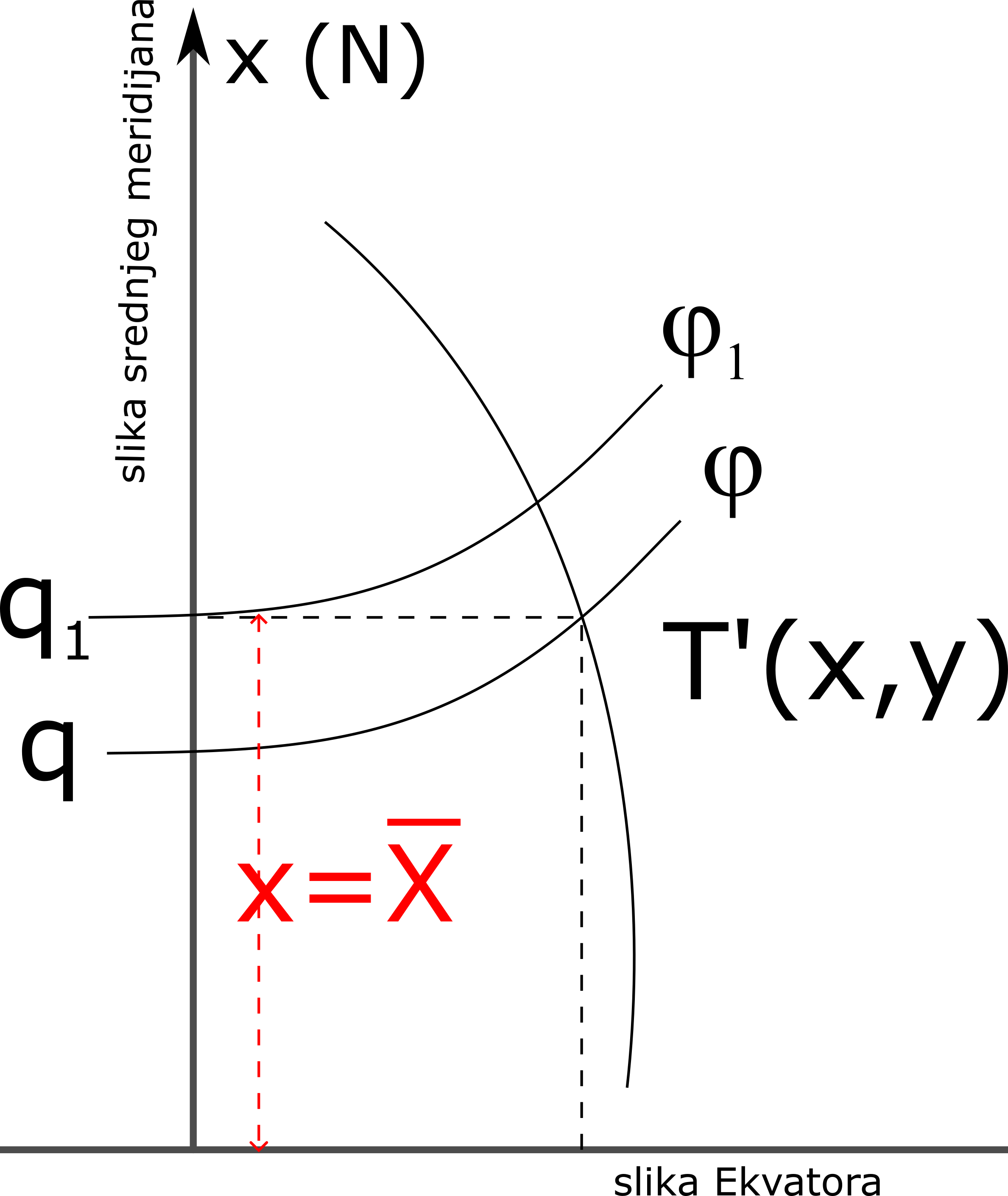
Kako širine meridijanskih zona ne prelaze \(6^o\), odnosno \(│l│ ≤ 3^o\) funkciju \(f(x+iy)\) možemo razviti u Tejlorov red, ako poznajemo njenu vrednost u okolini tačke \(q_1\):
\[ \begin{aligned} q+i l & =f(x)+i y \frac{d f(x)}{d x}+\frac{(i y)^2}{2} \frac{d^2 f(x)}{d x^2}+\frac{(i y)^3}{6} \frac{d^3 f(x)}{d x^3}+ \\ & +\frac{(i y)^4}{24} \frac{d^4 f(x)}{d x^4}+\frac{(i y)^5}{120} \frac{d^5 f(x)}{d x^5}+\frac{(i y)^6}{720} \frac{d^6 f(x)}{d x^6}+\ldots \end{aligned} \]
Prethodna formula se može preurediti znajući stepene imaginarne jedinice \(i\) i imajući u vidu relaciju \(q_1 = f(x)\), na sledeći način:
\[ \begin{aligned} q+i l & =q_1+i y\left(\frac{d q}{d X_1}\right)-\frac{y^2}{2}\left(\frac{d^2 q}{d \bar{X}^2}\right)_1-i \frac{y^3}{6}\left(\frac{d^3 q}{d \bar{X}^3}\right)_1+\frac{y^4}{24}\left(\frac{d^4 q}{d \bar{X}^4}\right)_1+ \\ & +i \frac{y^5}{120}\left(\frac{d^5 q}{d \bar{X}^5}\right)_1-\frac{y^6}{720}\left(\frac{d^6 q}{d \bar{X}^6}\right)_1+\ldots \end{aligned} \]
Izdvojimo li posebno realne, a posebno imaginarne članove, imamo:
\[ \begin{aligned} & q=q_1-\frac{y^2}{2}\left(\frac{d^2 q}{d \bar{X}^2}\right)_1+\frac{y^4}{24}\left(\frac{d^4 q}{d \bar{X}^4}\right)_1-\frac{y^6}{720}\left(\frac{d^6 q}{d \bar{X}^6}\right)_1+\ldots \\ & l=y\left(\frac{d q}{d \bar{X}}\right)_1-\frac{y^3}{6}\left(\frac{d^3 q}{d \bar{X}^3}\right)_1+\frac{y^5}{120}\left(\frac{d^5 q}{d \bar{X}^5}\right)_1-\ldots \end{aligned} \]
Tražene izvode možemo naći slično kao kod direktnog zadatka:
\[ \begin{aligned} & \frac{d q}{d \bar{X}}=\frac{d q}{d \varphi} \frac{d \varphi}{d \bar{X}} \\ & \frac{d^2 q}{d \bar{X}^2}=\frac{d}{d \varphi}\left(\frac{d q}{d \bar{X}}\right) \frac{d \varphi}{d \bar{X}} \\ & \frac{d^3 q}{d \bar{X}^3}=\frac{d}{d \varphi}\left(\frac{d^2 q}{d \bar{X}^2}\right) \frac{d \varphi}{d \bar{X}}, \text { itd. } \end{aligned} \]
Kako je (ovo smo radili kod konformne širine):
\[ d q=\frac{M \cdot d \varphi}{N \cos \varphi} \quad \Rightarrow \quad \frac{d \varphi}{d q} = \frac{Ncos \varphi}{ M } \]
A imamo isto da je:
\[ \bar{X}=\int_0^\varphi M \cdot d \varphi \quad \Rightarrow \frac{d \varphi}{d \bar{X}}=\frac{1}{M} \]
Dalje, za prvi izvod dobijamo:
\[ \frac{d q}{d \bar{X}}=\frac{M}{N \cos \varphi} \frac{1}{M}=\frac{1}{N \cos \varphi} \] Drugi izvod je:
\[ \frac{d^2 q}{d \bar{X}^2}=\frac{d}{d \varphi}\left(\frac{1}{N \cos \varphi}\right) \frac{1}{M}=\frac{\mathrm{M} \sin \varphi}{N^2 \cos ^2 \varphi} \frac{1}{M}=\frac{\operatorname{tan} \varphi}{N^2 \cos \varphi}=\frac{t}{N^2 \cos \varphi} \] Ostali izvodi:
\[ \begin{aligned} \frac{d^3 q}{d \bar{X}^3} & =\frac{1}{N^3 \cos \varphi}\left(1-2 t^2+\eta^2\right) \\ \frac{d^4 q}{d \bar{X}^4} &=\frac{t}{N^4 \cos \varphi}\left(5+6 t^2+\eta^2\right) \\ \frac{d^5 q}{d \bar{X}^5} &=\frac{1}{N^5 \cos \varphi}\left(5+28 t^2+24 t^4+6 \eta^2+8 \eta^2 t^2\right) \\ \frac{d^6 q}{d \bar{X}^6} &=\frac{t}{N^6 \cos \varphi}\left(61+180 t^2+120 t^4\right) \end{aligned} \]
U poslednjim jednačinama treba uočiti da su u izvodima četvrtog i petog reda odbačeni članovi sa \(η^4\), a u izvodima šestog reda članovi sa \(η^2\). Kada se dobijeni izvodi uvrste u izraze za Tejlorov red, imajući u vidu da se oni odnose na geografsku širinu \(\varphi_1\), dobijamo:
\[ \begin{aligned} q-q_1 &= -\frac{y^2}{2 N_1^2 \cos \varphi_1} t_1+\frac{y^4}{24 N_1^4 \cos \varphi_1} t_1\left(5+6 t_1^2+n_1^2\right)+ \\ &+\frac{y^6}{720 N_1^6 \cos \varphi_1} t_1\left(61+180 t_1^2+120 t_1^4\right) \\ l & =\frac{y}{N_1 \cos \varphi_1}-\frac{y^3}{6 N_1^3 \cos \varphi_1}\left(1+2 t_1^2+\eta_1^2\right)+ \\ &+\frac{y^5}{120 N_1^5 \cos \varphi_1}\left(5+28 t_1^2+24 t_1^4+6 \eta_1^2+8 \eta_1^2 t_1^2\right) . \end{aligned} \]
Principijelno uzimajući, rešen u celini. Druga od jednačina omogućava sračunavanje geografskih dužina na osnovu zadatih pravouglih koordinata \(x\) i \(y\) u projekciji. S druge strane, pošto je određena izometrička širina \(q\), može se reći da je određena geografska širina \(\varphi\).
Razlike širina su \(\Delta q = q - q_1\) i \(\Delta \varphi = \varphi - \varphi_1\) relativno male, jedna od razlika se može izraziti Tejlorovim redom aproksimacijom do drugog ili trećeg stepena.
\[ \begin{aligned} & \varphi-\varphi_1=\left(\frac{d \varphi}{d q}\right)_1\left(q-q_1\right)+ \\ & +\frac{1}{2}\left(\frac{d^2 \varphi}{d q^2}\right)\left(q-q_1\right)^2+\frac{1}{6}\left(\frac{d^3 \varphi}{d q^3}\right)_1\left(q-q_1\right). \end{aligned} \] Prvi izvod možemo odrediti: \[ d q=\frac{M \cdot d \varphi}{N \cos \varphi} \]
\[ \frac{d \varphi}{d q}=\frac{N \cos \varphi}{M}=\frac{1-e^2 \sin ^2 \varphi}{1-e^2} \cos \varphi=\left(1+e^{\prime 2} \cos ^2 \varphi\right) \cos \varphi=\left(1+\eta^2\right) \cos \varphi \] Drugi izvod:
\[ \begin{gathered} \frac{d^2 \varphi}{d q^2} \frac{d}{d \varphi}\left(\frac{d \varphi}{d q}\right) \frac{d \varphi}{d q}=\frac{d}{d \varphi}\left(\cos \varphi+n^2 \cos \varphi\right) \frac{d \varphi}{d q} \\ =\left(-\sin \varphi-3 e^{\prime} \sin \varphi \cos ^2 \varphi\right) \frac{d \varphi}{d q} \\ =-\sin \varphi \cos \varphi\left(1+3 \eta^2\right)\left(1+\eta^2\right)= \\ =-\operatorname{t cos}^2 \varphi\left(1+4 \eta^2+3 \eta^4\right) \end{gathered} \]
Sličnim postupkom dobija se treći izvod:
\[ \frac{d^3 \varphi}{d q^3}=-\cos ^3 \varphi\left(1-t^2\right) \]
Definitivno rešenje dobijamo kad izvode
\[ \frac{d^n \varphi}{d q^n}, \quad n=1,2,3 \ldots \]
kao i stepene razlika \((q-q1)\) uvrstimo u prethodni Tejlorov red za izraz (\(\varphi - \varphi1\)), potom ovaj izraz sredimo, te sa već navedenim izrazom za l konačno dobijamo:
\[ \varphi=\varphi_1-\frac{y^2}{2 M_1 N_1} t_1+\frac{y^4}{24 M_1 N_1^3} t_1\left(5+3 t_1^2+\eta_1^2-9 \eta_1^2 t_1^2\right)-\frac{y^6}{720 M_1 N_1^5} t_1\left(61+90 t_1^2+45 t_1^4\right) \]
\[ l=\frac{y}{N_1 \cos \varphi_1}-\frac{y^3}{6 N_1^3 \cos \varphi_1}\left(1+2 t_1^2+\eta_1^2\right)+\frac{y^5}{120 N_1^5 \cos \varphi_1}\left(5+28 t_1^2+24 t_1^4+6 \eta_1^2+8 \eta_1^2 t_1^2\right) \]
Pri čemu se \(\varphi_1\) može sračunati kao (Snyder (1987)):
\[ \begin{aligned} &\begin{aligned} \varphi_1= & \mu+\left(3 e_2 / 2-27 e_2^3 / 32+\ldots\right) \sin 2 \mu+\left(21 e_2^2 / 16\right. \\ & \left.-55 e_2^4 / 32+\ldots\right) \sin 4 \mu+\left(151 e_2^3 / 96+\ldots\right) \sin 6 \mu+\left(1097 e_2^4 / 512-\ldots\right) \\ & \sin 8 \mu+\ldots \end{aligned}\\ &\begin{aligned} & e_2=\left[1-\left(1-e^2\right)^{1 / 2}\right] /\left[1+\left(1-e^2\right)^{1 / 2}\right] \\ & \mu= L_m /\left[a\left(1-e^2 / 4-3 e^4 / 64-5 e^6 / 256-\ldots\right)\right] \\ & L_m=\bar{X}(\varphi_0)+y / m_0 \\ & \text{gde je } m_0 \text{ razmera duž sr. mer. za izvornu GK } m_0 = 1 , \\ &\text{za Srbiju } m_0 = 0.9999, \\ &\text{za UTM } m_0 = 0.9996. \end{aligned} \end{aligned} \]
Neophodan je iterativni postupak koji brzo konvergira od \(\varphi_0\) do \(\varphi_1\).
Formule se mogu zapisati i u obliku:
\[ \begin{gathered} \varphi=\varphi_1-B_2 y^2+B_4 y^4-B_6 y^6 \\ l=B_1 y-B_3 y^3+B_5 y^5 \end{gathered} \]
\[ \begin{gathered} B_1=\frac{\rho}{N_1 \cos \varphi_1} \\ B_2=\frac{\rho}{2 M_1 N_1} t_1 \\ B_3=\frac{\rho}{6 N_1^3 \cos \varphi_1}\left(1+2 t_1^2+\eta_1^2\right) \\ B_4=\frac{p}{24 M_1 N_1^3} t_1\left(5+3 t_1^2+n_1^2-9 n_1^2 t_1^2\right) \\ B_5=\frac{\rho}{120 N_1^5 \cos \varphi_1}\left(5+28 t_1^2+24 t_1^4+6 \eta_1^2+8 \eta_1^2 t_1^2\right) \\ B_6=\frac{\rho}{720 M_1 N_1^5} t_1\left(61+90 t_1^2+45 t_1^4\right) \end{gathered} \]
7.3 Određivanje širine zone preslikavanja
- Širina zone preslikavanja, odnosno veličina područja koje se može preslikati u jednom koordinatnom sistemu, zavisi od tačnosti koju zahtevamo od projekcije.
- Kako kod konformnih projekcija nema deformacija uglova, to linearna deformacija predstavlja glavni kriterijum.
- Imajuću u vidu prethodno razmatranu funkciju linearne razmere, problem određivanja širine zone preslikavanja svodi se na na određivanje maksimalne vrednosti redukovane geodetske dužine \(l_{max}\) za koju linearna razmera dostiže maksimalno dozvoljenu vrednost \(cl_{max}\), koja je unapred zadata.
- Kriterijum linearne tačnosti definisan je na osnovu propisane relativne tačnosti merenja dužina u poligonskoj mreži od 1:3.000 (tačnost dužina je u trigonometrijskoj mreži IV reda oko 1:10.000), te je za kriterijum tačnosti projekcije uzeta vrednost od 1:10.000.
- Na taj način, ako su greške projekcije 3 puta manje od grešaka masovnih linearanih merenja u radovima na premeru, smatralo se da se deformacije dužina mogu zanemariti.
Određivanje širine zone za zadati uslov linearnih deformacija 1 dm/km
Za geodetske širine 30, 40, 45, 50 i 60 stepeni severne geodetske širine odredićemo širinu zone uz uslov da linearne deformacije ne prelaze 1 dm/km. Vratimo se prvo na formulu za računanje linearne razmere:
\[ \begin{aligned} C_1 & =\frac{\cos ^2 \varphi}{2 \rho^2}\left(1+\eta^2\right) \\ C_2 & =\frac{\cos ^4 \varphi}{24 \rho^4}\left(5-4 t^2\right)\\ c& =1+C_1 l^2+C_2 l^4 \end{aligned} \]
Imamo da linearna deformacija ne prelazi 1 dm/km, kako je \(dc=c-1=C_1 l^2+C_2 l^4\), član \(C_2\) uz redukovanu dužinu na 4. stepenu možemo zanemariti. Tako da možemo odrediti graničnu vrednost redukovane dužine koja ispunjava ovaj uslov na sledeći način:
\[ 0.0001=\frac{l^2}{2 \rho^2}\left(1+\eta^2\right) \cos ^2 \varphi \]
Odavde je:
\[ l=\frac{\rho \sqrt{0.0002}}{\sqrt{1+\eta^2} \cos \varphi} \]
options( digits = 12)
fi = c(30, 40, 45, 50, 60)*pi/180
# Beselov elipsoid
a=6377397.155
rf=299.1528128
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
# b=6356078.9628181880963
# e1= sqrt((a^2-b^2)/b^2)
t=tan(fi)
eta=e1*cos(fi)
ro=180/pi
l= ro*sqrt(0.0002)/ (sqrt(1+eta^2) * cos(fi) )
# funkcija za stepen u stepen minut sekund
deg2dms <- function(deg){
deg_sign = sign(deg)
deg = abs(deg)
DEG = floor(deg)
MIN = floor((deg - DEG) * 60)
SEC = (deg - DEG - MIN/60) * 3600
SEC=round(SEC,2)
dms=paste(deg_sign*DEG,'\u00B0',MIN,"'",SEC,"''",sep='')
return(dms)
}
df =data.frame(Latituda = round(fi*180/pi ),
lmax = l,
lmax_dms= deg2dms(l),
lon_21_min = deg2dms(21-l),
lon_21_max = deg2dms(21+l) )
knitr::kable( df , align = "c", row.names = FALSE,
format.args = list(scientific = FALSE, format = "f") )| Latituda | lmax | lmax_dms | lon_21_min | lon_21_max |
|---|---|---|---|---|
| 30 | 0.933287505617 | 0°55’59.84’’ | 20°4’0.16’’ | 21°55’59.84’’ |
| 40 | 1.055672323504 | 1°3’20.42’’ | 19°56’39.58’’ | 22°3’20.42’’ |
| 45 | 1.143995512549 | 1°8’38.38’’ | 19°51’21.62’’ | 22°8’38.38’’ |
| 50 | 1.258833003120 | 1°15’31.8’’ | 19°44’28.2’’ | 22°15’31.8’’ |
| 60 | 1.619209961476 | 1°37’9.16’’ | 19°22’50.84’’ | 22°37’9.16’’ |
7.4 Stari državni koordinatni sistem (DKS) u Srbiji
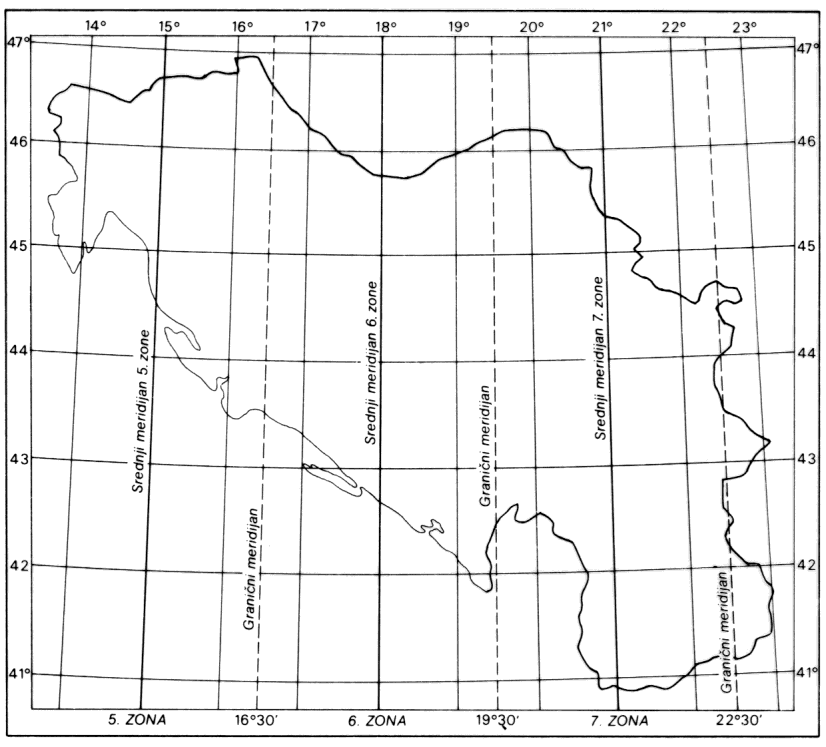
Marta 1924. Stručna komisija je Gaus-Krigerovu projekciju usvojila (među prvima u Evropi) za projekciju premera državne teritorije Jugoslavije. Za srednje meridijane usvojeni su: \(15^o, 18^o, 21^o\), odnosno 3 koordinatna sistema, Slika 7.10. Usvojene su tri zone: 5, 6, 7, sa srednjim meridijanima po zonama: \(15^o, 18^o, 21^o\). Granični meridijani među zonama su: \(16.5^o\), \(19.5^o\) i oko \(22.5^o\).
7.5 Redukcija koordinata
Ako se uvede uslov da na srednjem meridijanu linearna deformacija iznosi -0.0001, odnosno linearna razmera 0.9999, onda i vrednosti koordinata koje su takođe linearne veličine treba pomnožiti faktorom \(m_0=0.9999\). Faktor \(m_0\) nazivamo linearnim modulom, a koordinate pomnožene ovim faktorom redukovanim koordinatama (modulisanim koordinatama).
\[ \begin{aligned} & x=m_0 \bar{x}=(1-0,0001) \bar{x}=0,9999 \bar{x} \\ & y=m_0 \bar{y}=(1-0,0001) \bar{y}=0,9999 \bar{y} \end{aligned} \]
Apscise (\(x\)) su uvek pozitivne, dok su ordinate (\(y\)) pozitivne za tačke istočno od srednjeg meridijana, negativne za tačke zapadno od srednjeg meridijana.
Da bi se izbegle negativne vrednosti ordinata, svim ordinatama dodaje se 500.000 metara, po predlogu nemačkog geodete Baumgarta.
Da bi se obezbedila jednoznačnost koordinata, ispred vrednosti ordinate dodaje se broj koordinatnog sistema, odnosno npr. u 7. zoni dodaje se 7.000.000. tako da je za 7. zonu to ukupno 7.500.000, za 6. zonu 6.500.000 i za petu zonu 5.500.000
\[ \begin{aligned} & x=m_0 \bar{x}=(1-0,0001) \bar{x}=0,9999 \bar{x} \\ & y=7500000+m_0 \bar{y}=7500000+(1-0,0001) \bar{y}=7500000+0,9999 \bar{y} \end{aligned} \]
Koordinatni referentni sistem u Gaus-Krigerovoj projekciji za Srbiju sa datumom Hermanskogel je definisan u proj4 notaciji na sledeći način:
+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=mZadat je koordinatni referentni sistem u Gaus-Krigerovoj projekciji za Srbiju, sa sledećim parametrima:
+proj=tmerc #Gaus Kriger (Transverzalna merkatorova) projekcija,
+lat_0=0 +lon_0=21 # koordinatni početak na elipsoidu,
+k=0.9999 # razmera duž srednjeg meridijana,
+x_0=7500000 +y_0=0 # koord. početak u ravni karte pravac ist. i sev.
+ellps=bessel # elipsoid
+towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89
# Parametri geodetskog datuma Hermanskogel
# 3 translacije, 3 rotacije,
# razmera u odnosu na WGS84 izražena u ppm (parts per milion) +=m - jedinice metri.Širina zone za stari DKS u Srbiji
Za geodetske širine 30, 40, 45, 50 i 60 stepeni severne geodetske širine odredićemo širinu zone uz uslov da linearne deformacije ne prelaze 1 dm/km. Vratimo se prvo na formulu za računanje linearne razmere:
\[ \begin{aligned} C_1 & =\frac{\cos ^2 \varphi}{2 \rho^2}\left(1+\eta^2\right) \\ C_2 & =\frac{\cos ^4 \varphi}{24 \rho^4}\left(5-4 t^2\right)\\ c& =m_0 (1+C_1 l^2+C_2 l^4) \end{aligned} \]
Imamo da linearna deformacija ne prelazi 1 dm/km, kako je \(dc=c-1=0.9999+0.9999C_1 l^2+0.9999C_2 l^4 -1\), član \(C_2\) uz redukovanu dužinu na 4. stepenu možemo zanemariti. Tako da možemo odrediti graničnu vrednost redukovane dužine koja ispunjava ovaj uslov na sledeći način:
\[ 0.0001=-0.0001+\frac{l^2}{2 \rho^2}\left(1+\eta^2\right) \cos ^2 \varphi \] Odavde je:
\[ l=\frac{\rho \sqrt{0.0004}}{\sqrt{1+\eta^2} \cos \varphi}=\frac{\rho 0.02}{\sqrt{1+\eta^2} \cos \varphi} \]
options( digits = 12)
fi = c(30, 40, 45, 50, 60)*pi/180
# Beselov elipsoid
a=6377397.155
rf=299.1528128
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
# b=6356078.9628181880963
# e1= sqrt((a^2-b^2)/b^2)
t=tan(fi)
eta=e1*cos(fi)
ro=180/pi
l= ro*0.02/ (sqrt(1+eta^2) * cos(fi) )
# funkcija za stepen u stepen minut sekund
deg2dms <- function(deg){
deg_sign = sign(deg)
deg = abs(deg)
DEG = floor(deg)
MIN = floor((deg - DEG) * 60)
SEC = (deg - DEG - MIN/60) * 3600
SEC=round(SEC,2)
dms=paste(deg_sign*DEG,'\u00B0',MIN,"'",SEC,"''",sep='')
return(dms)
}
df =data.frame(Latituda = round(fi*180/pi ),
lmax = l,
lmax_dms= deg2dms(l),
lon_21_min = deg2dms(21-l),
lon_21_max = deg2dms(21+l) )
knitr::kable( df , align = "c", row.names = FALSE,
format.args = list(scientific = FALSE, format = "f") ) | Latituda | lmax | lmax_dms | lon_21_min | lon_21_max |
|---|---|---|---|---|
| 30 | 1.31986784804 | 1°19’11.52’’ | 19°40’48.48’’ | 22°19’11.52’’ |
| 40 | 1.49294611732 | 1°29’34.61’’ | 19°30’25.39’’ | 22°29’34.61’’ |
| 45 | 1.61785396914 | 1°37’4.27’’ | 19°22’55.73’’ | 22°37’4.27’’ |
| 50 | 1.78025870577 | 1°46’48.93’’ | 19°13’11.07’’ | 22°46’48.93’’ |
| 60 | 2.28990868785 | 2°17’23.67’’ | 18°42’36.33’’ | 23°17’23.67’’ |
Dakle, vidimo da je širina zone za područje oko srednje geodetske širine \(45^o\) oko \(1.5^o\), a da je pritom ispunjen uslov da se dužine ne deformišu više od 1 dm/km, to je i razlog zašto je za stari DKS usvojeno da je širina zone \(3^o\), odnosno \(1.5^o\) istočno i zapadno od srednjeg meridijana. Iako 7. zona ne pokriva deo istočne Srbije, ona se koristi ne uvodeći 8. zonu. Za deo Zapadne Srbije koristi se i 6. zona.
Sledeća karta prikazuje elipse deformacija sa sračunatom linearnom deformacijom u dm po km, Slika 7.11.
library(sf)
# kreiramo tačke u kojima cemo prikazati elipse deformacija
lonlat = rbind(c(19,42), c(19,44), c(19,46),
c(20,42), c(20,44), c(20,46),
c(21,42), c(21,44), c(21,46),
c(22,42), c(22,44), c(22,46) ,
c(23,42), c(23,44), c(23,46) )
tissot.pt <- st_sfc( st_multipoint(lonlat),
crs = 4326) # WGS84 koordinatni ref. sis.
tissot.pt <- st_cast(tissot.pt, "POINT")
# konvertujemo u single point geometriju
# plot(tissot.pt)
# koristi se s2 paket za elipsodna računanja
# Pravimo tacke po krugu udaljene 30 km od centra elipse
tissot.sf = st_buffer(tissot.pt, dist = 30000, max_cells = 1000)
# max_cells
# The maximum number of cells to approximate a buffer.
# nrow(st_coordinates(tissot.sf[1]))
# [1] 646
# Ako koristimo opciju max_cell = 1000 imamo 646 prelomnih tačaka poligona
# konvertujemo kolekciju poligona u sf objekat
tissot.sf <- st_sf(tissot.sf)
gk_srb = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
tissot.gk <- st_transform(tissot.sf, gk_srb)
lr <- function(lonlatmatrica){
l= (lonlatmatrica[,1] -21)*pi/180
fi= (lonlatmatrica[,2])*pi/180
# GRS80 a=6378137.0 rf=298.257222101 GRS 1980(IUGG, 1980)
a=6378137.0
rf=298.257222101
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
t=tan(fi)
eta=e1*cos(fi)
C1=1/2*(1+eta^2)*(cos(fi))^2
C2=1/24*(5-4*t^2)*(cos(fi))^4
# linerarna razmera (u R-u se uglavnom ne koristi c kao promenljiva)
cc=0.9999*(1+C1*l^2+C2*l^4)
return(cc)
}
# linerarna deformacija u dm/km
tissot.gk$dc <- (lr(lonlat)-1) *1000*10
url=paste('http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs',
'?service=WFS&version=1.0.0&',
'request=GetFeature&typeName=osgl_4:POP_age',sep='')
download.file(url, 'poage.gml')
pop = st_read('poage.gml')
# Reading layer `POP_age' from data source `C:\mk_knjiga\poage.gml' using driver `GML'
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# CRS: NA
st_crs(pop) = 4326
pop = st_transform(pop, gk_srb )
ll = st_centroid(tissot.gk)
ll = st_coordinates(ll)
# 7 zona
pts1 = cbind( rep(19.5,100) , seq(40,48,length.out = 100) )
pts2 = cbind( rep(21.5,100) , seq(40,48,length.out = 100) )
ls1 = st_linestring(pts1)
ls2 = st_linestring(pts2)
stp = st_sfc(ls1,ls2, crs ="+proj=longlat +ellps=GRS80 +datum=WGS84" )
stp = st_transform(stp,
gk_srb)
# Karta sa elipsama deformacija i deformacijom dužina dm/km
plot(st_geometry(pop), graticule = TRUE, col= 'gray', border ='black', axes = TRUE)
plot(stp, col ='blue', add = TRUE) # 7 zona
plot(st_geometry(tissot.gk),
border = rgb(44/255,127/255,184/255,0.5),
col=rgb(44/255,127/255,184/255,0.5),
add = TRUE)
text(ll[, 1], ll[, 2], paste("dc=",round(tissot.gk$dc,2)) ,col='red' , cex = 0.8)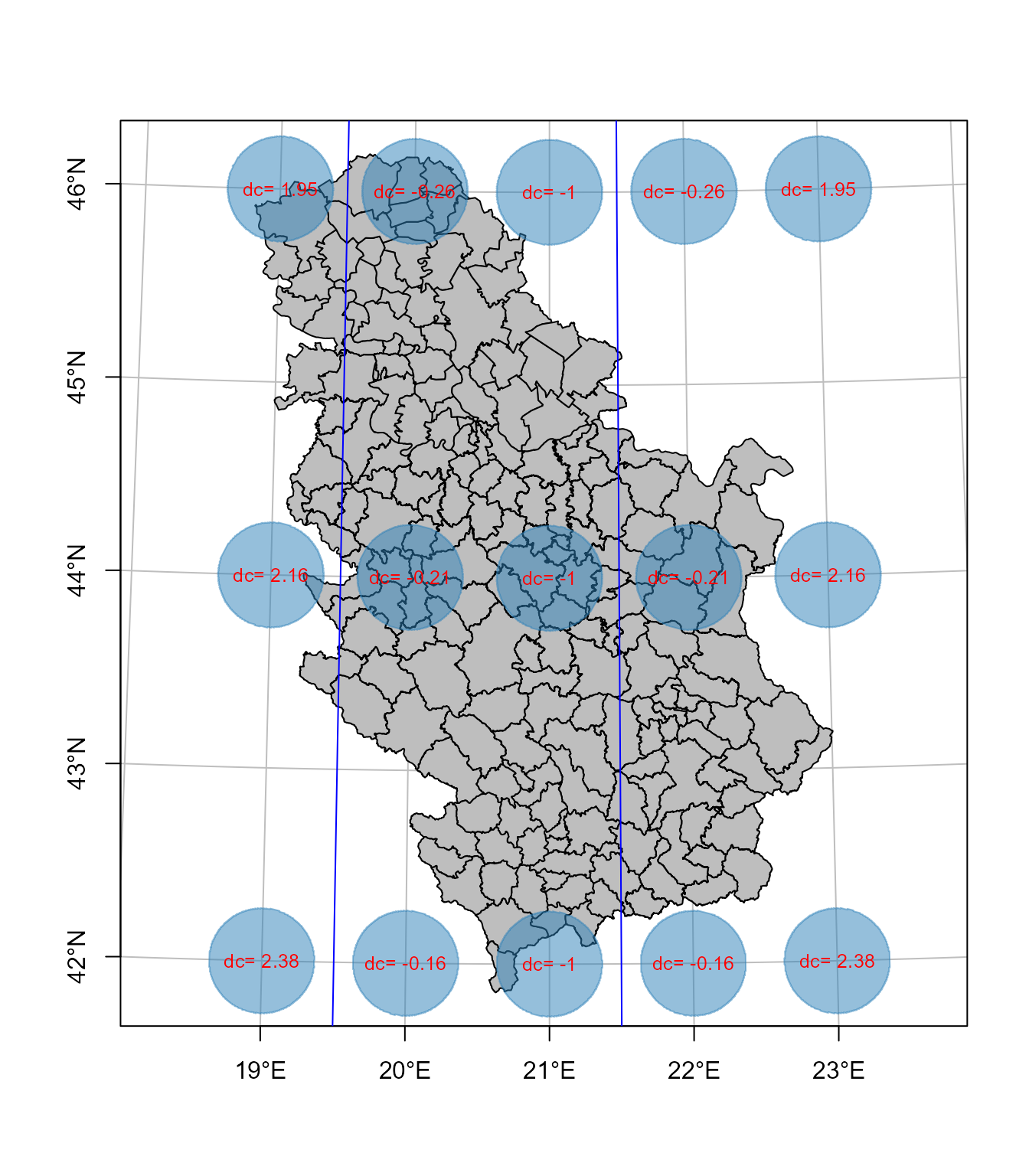
7.6 Značaj Gaus-Krigerove projekcije
Deo koji se odnosi na istorijski značaj Gaus-Krigerove projekcije baziran na knjizi Matematička kartografija, Jovanović (1984).
Projekcija se naziva Gaus-Krigerovom jer je njenu osnovnu teoriju razvio Gaus, a radne formule razvio je Kriger. Carl Friedrich Gauss (1777‒1855), poznati nemački naučnik i profesor Univerziteta u Getingemu, poznat je po svojim delima iz oblasti matematike, astronomije, geodezije i fizike, koja se i danas smatraju fundamentalnim radovima u ovim oblastima nauke. Gaus je prvi put svoju metodu direktnog preslikavanja elipsoida na ravan primenio za izravnanje trigonometrijske mreže grada Hanovera.
Ovu metodu Gaus nije objavio, ali je posle njegove smrti prof. Kriger (Louis Krüger (1857‒1923), nemački profesor geodezije) pregledao Gausovu zaostavštinu po nalogu Naučnog društva iz Getingema radi konačnog objavljivanja, te je obavio temeljnu obradu Gausove metode i publikovao je 1912. godine. Ovu projekciju za državnu prva je usvojila Austrija 1917. godine, zatim Nemačka 1922. (1923) godine, dok se u našoj zemlji ona koristi od 1924. godine. Gaus-Krigerova projekcija se, zbog svojih dobrih osobina, primenjuje gotovo u svim zemljama Sveta za geodetsko-kartografske radove. U SSSR-u se koristi od 1928. godine, kako za geodetske potrebe, tako i za izradu topografskih karata do razmere 1:500.000. U nizu zapadnoevropskih zemalja i SAD primenjuje se nešto modifikovana Gaus-Krigerova projekcija poznata kao Univerzalna poprečno Merkatorova projekcija (Universal Transverse Mercator Projection), tzv. UTM projekcija, koja će biti opisana u narednom poglavlju.
7.7 Primeri u Gaus-Krigerovoj projekciji
Primer 1: Računanje koordinata jedne tačke, direktni zadatak
Elipsoidne koordinate pozicije Građevinskog fakulteta u Beogradu (\(\varphi=44.80574931245\) i \(\lambda=20.4813687832\)) iz koordinatnog sistema na elipsoidu Besel sa datumom Hermanskogel transformisati u Gaus-Krigerovu projekciju (stari DKS Srbija).
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = st_point( c(20.4813687832, 44.80574931245) ) # lon , lat
# potom pravimo kolekciju geometrije sfc u odgovarajućoj projekciji
bes_crs = "+proj=longlat +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89"
pts_sfc = st_sfc(grf, crs=bes_crs)
# GK Srb koord. ref. sis.
gk_srb = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
# transformacija u GK
pts_sfc_gk = st_transform(pts_sfc, crs =gk_srb)
pts_sfc_gk
# Geometry set for 1 feature
# Geometry type: POINT
# Dimension: XY
# Bounding box: xmin: 7458978.69593 ymin: 4962489.15422 xmax: 7458978.69593 ymax: 4962489.15422
# Projected CRS: +proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m
# matrica koordinata iz prostornih podataka
st_coordinates(pts_sfc_gk)
# X Y
# [1,] 7458978.69593 4962489.15422
# koordinate treba zaokružiti do na cm
round(st_coordinates(pts_sfc_gk),2)
# X Y
# [1,] 7458978.7 4962489.15
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import shapely.geometry
import geopandas as gpd
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
grf = shapely.geometry.Point(20.4813687832, 44.80574931245)
# potom pravimo kolekciju geometrije sa koor. ref.sis
bes_crs = "+proj=longlat +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89"
grf_geom_proj = gpd.GeoSeries([grf], crs=bes_crs)
# prostorni lejer
grf_layer_proj = gpd.GeoDataFrame({'geometry': grf_geom_proj})
# GK Srb koord. ref. sis.
gk_srb = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
# transformacija u GK projekciju
grf=grf_layer_proj.to_crs(gk_srb)
print(grf)
# geometry
# 0 POINT (7458978.696 4962489.154)Primer 2: Grafik deformacija u zavisnosti od geodetske dužine za fiksiranu geodetsku širinu
Napraviti grafik deformacije dužina izražene u dm/km u zavisnosti od geodetske dužine za fiksiranu geodetsku širinu na \(\varphi=43^o\) u Gaus-Krigerovoj projekciji za Srbiju (stari DKS).
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
fi = 43*pi/180
# redukovane širine za koje računamo deformacije
l=(seq(21,23,by=0.2) -21)*pi/180
# Beselov elipsoid
a=6377397.155
rf=299.1528128
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
# b=6356078.9628181880963
# e1= sqrt((a^2-b^2)/b^2)
t=tan(fi)
eta=e1*cos(fi)
C1=1/2*(1+eta^2)*(cos(fi))^2
C2=1/24*(5-4*t^2)*(cos(fi))^4
# linerarna razmera (u R-u se uglavnom ne koristi c kao promenljiva)
cc=0.9999*(1+C1*l^2+C2*l^4)
# linerarna deformacija
dc=cc-1
# linerarna deformacija u dm/km
dc_dm_km = round( dc *1000*10 ,1)
plot(21+l*180/pi ,dc_dm_km, main = "Lin. def. u zavisnosti od geod. duž.",
xlab = parse(text = "lambda"),
ylab = "Linearna deformacija u dm/km",type = "l")
grid()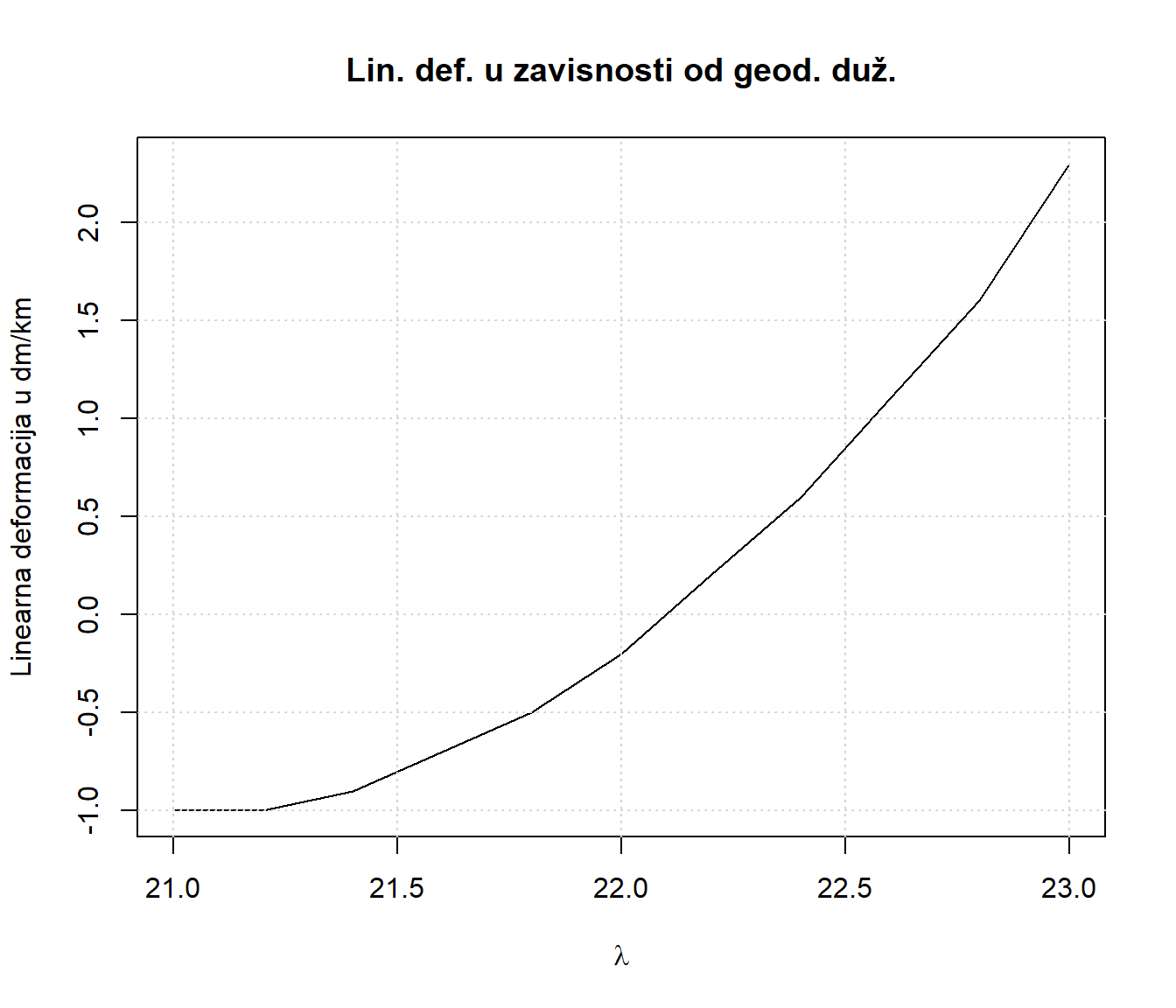
import numpy as np
import matplotlib.pyplot as plt
fi = 43 * np.pi / 180
# redukovana geod. dužina
l = (np.arange(21, 23.1, 0.2) - 21) * np.pi / 180
# elipsoid Bessel
a = 6377397.155
rf = 299.1528128
f = 1 / rf
e = np.sqrt(2 * f - f ** 2)
e1 = np.sqrt((2 * f - f ** 2) * (1 - f) ** -2)
# b = 6356078.9628181880963
# e1 = np.sqrt((a ** 2 - b ** 2) / b ** 2)
t = np.tan(fi)
eta = e1 * np.cos(fi)
C1 = 1 / 2 * (1 + eta ** 2) * (np.cos(fi)) ** 2
C2 = 1 / 24 * (5 - 4 * t ** 2) * (np.cos(fi)) ** 4
# linearna razmera
c= 0.9999 * (1 + C1 * l ** 2 + C2 * l ** 4)
# linearna deformacija
dc = c - 1
# linearna deformocija dm/km
dc_dm_km = np.round(dc * 1000 * 10, 1)
plt.plot(21 + l * 180 / np.pi, dc_dm_km)
plt.title("Lin. def. u zavisnosti od geod. duž.")
plt.xlabel(r"$\lambda$")
plt.ylabel("Linearna deformacija u dm/km")
plt.grid()
plt.show()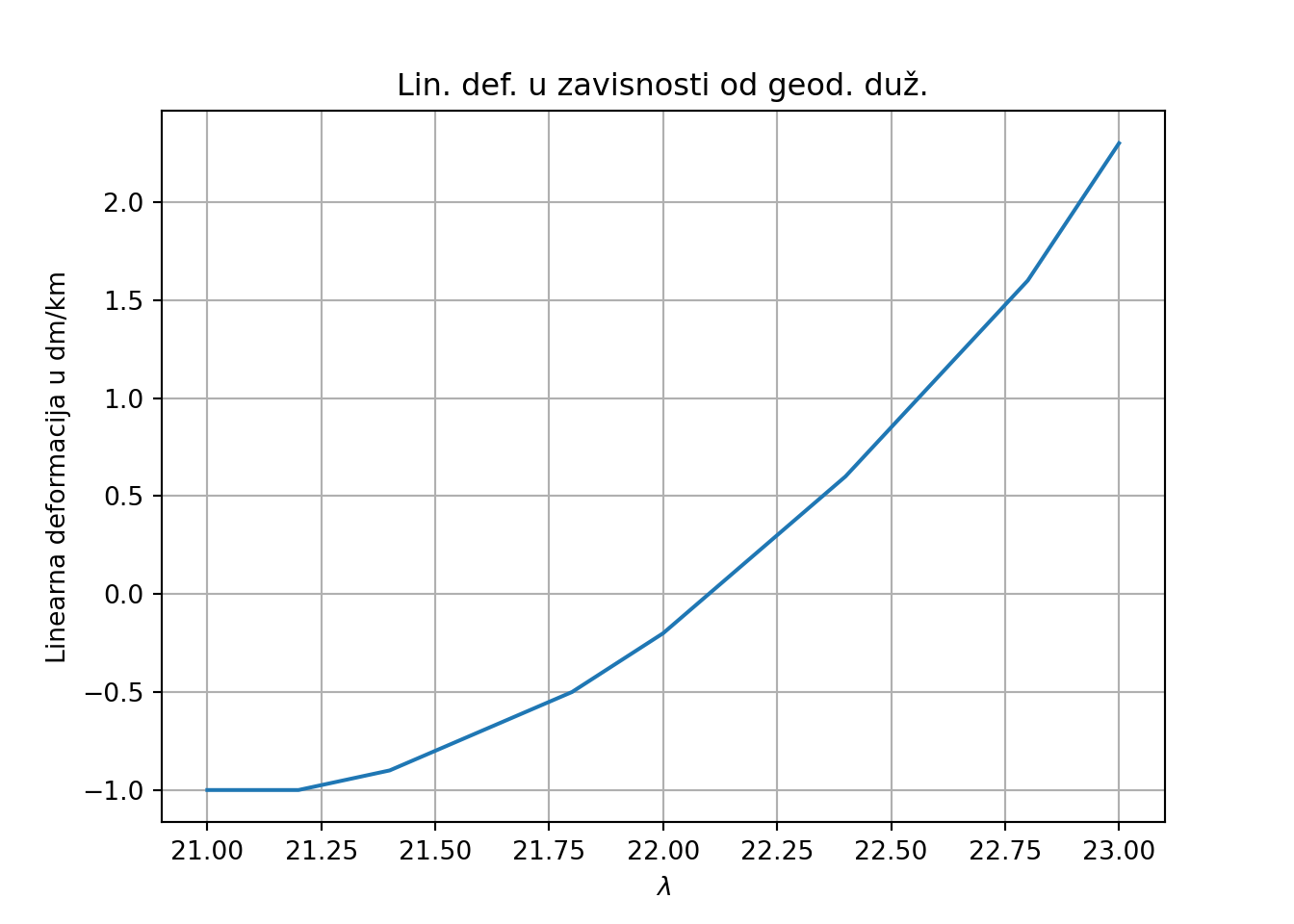
Primer 3: Napraviti kartu izokola u Gaus-Krigerovoj projekciji
Napraviti kartu izokola, sa vrednostima deformacija dužina izraženim u dm/km u Gaus-Krigerovoj projekciji za Srbiju (stari DKS).
library(terra)
bbox= ext(c(18.81499446, 23.00637464, 41.85209979, 46.19005677 ) )
#(xmin, xmax, ymin, ymax)
# prazan raster
er <- rast(bbox, resolution=0.00833 )
# 0.00833 * 6377000*pi/180 oko 1 km rezolucija
# koordinate za svaki piksel rastera
l <- ( init(er, 'x') -21) *pi/180
fi <- init(er, 'y') *pi/180
# Beselov elipsoid
a=6377397.155
rf=299.1528128
f = 1/rf
e = sqrt(2*f - f^2)
e1 = sqrt( (2*f - f^2)*(1 - f)^-2 )
# b=6356078.9628181880963
# e1= sqrt((a^2-b^2)/b^2)
t=tan(fi)
eta=e1*cos(fi)
C1=1/2*(1+eta^2)*(cos(fi))^2
C2=1/24*(5-4*t^2)*(cos(fi))^4
# linerarna razmera (u R-u se uglavnom ne koristi c kao promenljiva)
cc=0.9999*(1+C1*l^2+C2*l^4)
# linerarna deformacija
dc=cc-1
# linerarna deformacija u dm/km
dc_dm_km = round( dc *1000*10 ,1)
plot(dc_dm_km, main="Izokole, deformacije dužina dm/km")
contour(dc_dm_km, add=TRUE, nlevels = 15)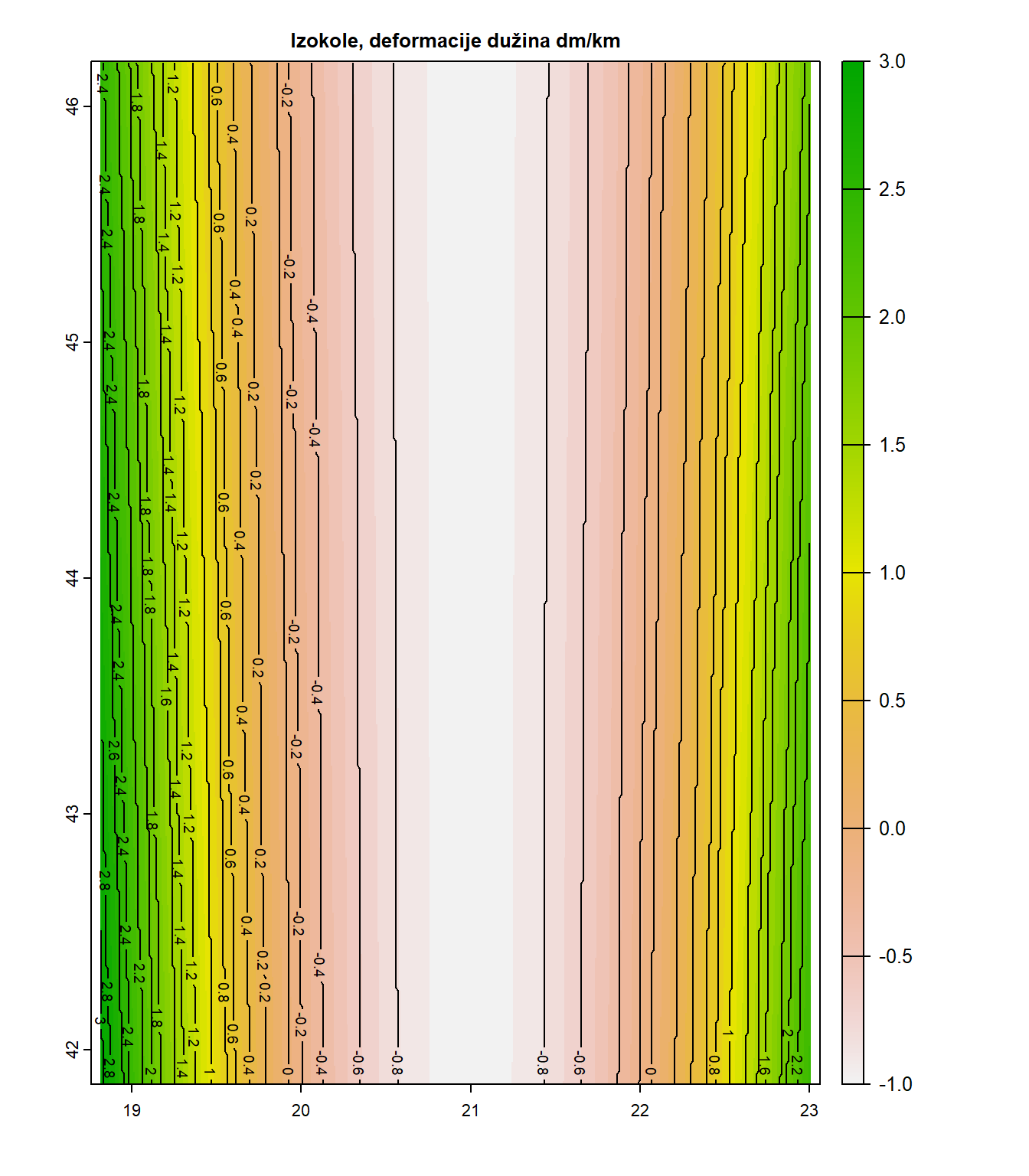
import numpy as np
import rasterio
from rasterio.plot import show
import matplotlib.pyplot as plt
import os
# okvir
bbox = (18.81499446, 23.00637464, 41.85209979, 46.19005677)
# raster sa zadatom rezolucijom
resolution = 0.00833
width = int((bbox[1] - bbox[0]) / resolution)
height = int((bbox[3] - bbox[2]) / resolution)
transform = rasterio.transform.from_origin(bbox[0], bbox[3], resolution, resolution)
er = np.zeros((height, width))
height = er.shape[0]
width = er.shape[1]
cols, rows = np.meshgrid(np.arange(width), np.arange(height))
xs, ys = rasterio.transform.xy(transform, rows, cols)
lons= np.array(xs)
lats = np.array(ys)
# lon lat matrice
l = (lons - 21) * np.pi / 180
fi = lats * np.pi / 180
# Beselov elipsoid
a = 6377397.155
rf = 299.1528128
f = 1 / rf
e = np.sqrt(2 * f - f ** 2)
e1 = np.sqrt((2 * f - f ** 2) * (1 - f) ** -2)
t = np.tan(fi)
eta = e1 * np.cos(fi)
C1 = 1 / 2 * (1 + eta ** 2) * (np.cos(fi)) ** 2
C2 = 1 / 24 * (5 - 4 * t ** 2) * (np.cos(fi)) ** 4
# linearna razmera
cc = 0.9999 * (1 + C1 * l ** 2 + C2 * l ** 4)
# linearna deformacija
dc = cc - 1
# linearna deformacija dm po km
dc_dm_km = np.round(dc * 1000 * 10, 1)
rio_arr = rasterio.open('tmp.tif',driver='GTiff', mode='w',
height=height,
width=width,
count=1,
dtype=dc_dm_km.dtype,
transform=transform)
rio_arr.write(dc_dm_km,1)
rio_arr.close()
rio_arr = rasterio.open('tmp.tif')
fig, ax = plt.subplots()
show(rio_arr, ax =ax, cmap="terrain")
show(rio_arr, contour=True,ax=ax, colors="black")
plt.show()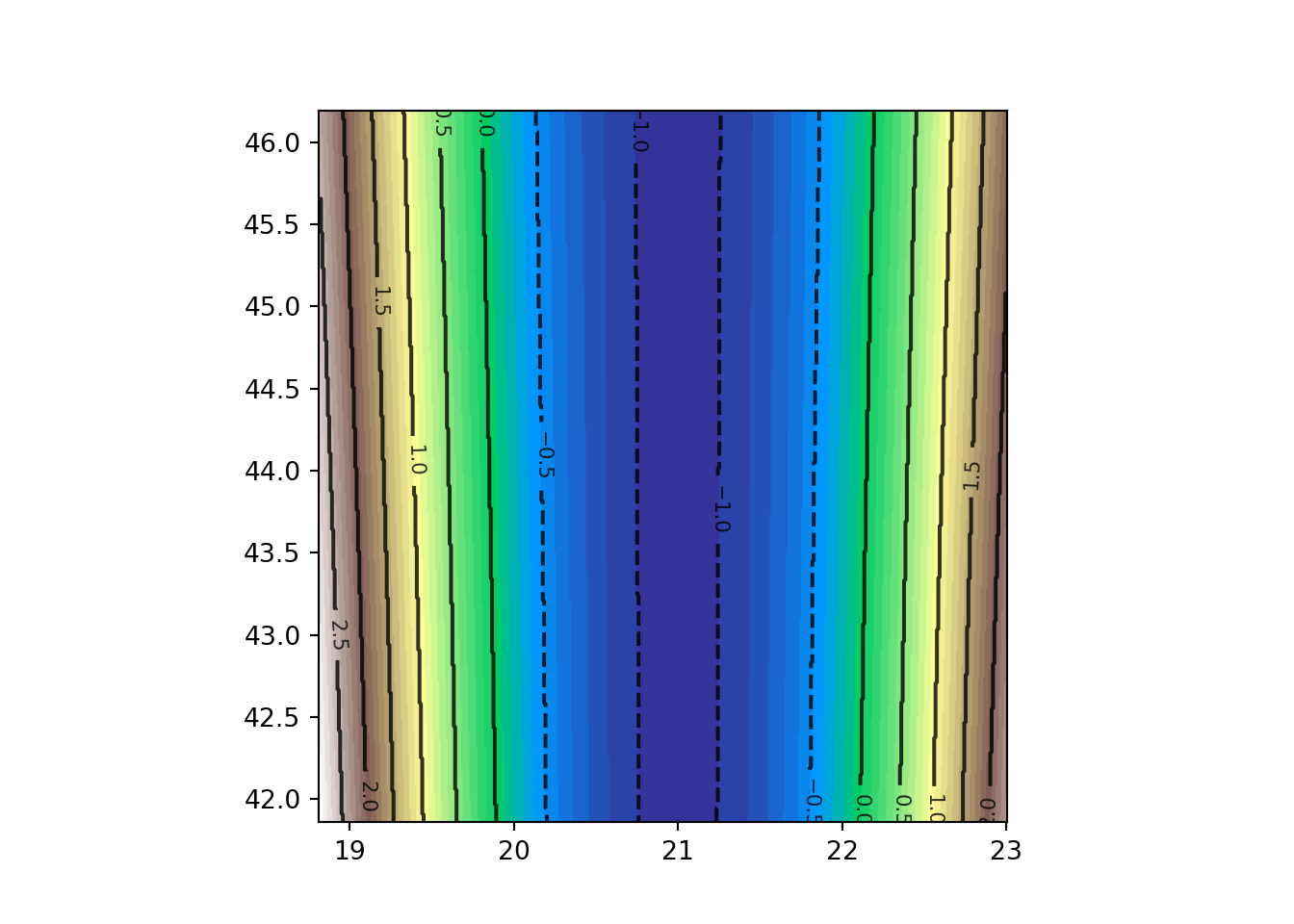
# os.remove("tmp.tif")Primer 4: Transformacija vektorskih podataka iz WGS84 u GK (DKS)
Transformisati poligone opština u Srbiji u Gaus-Krigerovu projekciju (DKS). U pozadini procesa se dešava i datumska transformacija iz datuma WGS84 u datum Hermanskogel zadat sa 7 parametara geocentričnog datuma. Poligoni opština se mogu preuzeti kroz WFS servis laboratorije za razvoj softvera otvorenog koda na Građevinskom fakultetu, OSGL Beograd.
library(sf)
# granice opština u Srb
url=paste('http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs',
'?service=WFS&version=1.0.0&',
'request=GetFeature&typeName=osgl_4:POP_age',sep='')
download.file(url, 'poage.gml')
pop = st_read('poage.gml')
# Reading layer `POP_age' from data source `C:\mk_knjiga\poage.gml' using driver `GML'
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# CRS: NA
st_crs(pop) = 4326
pop
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 18.8 ymin: 41.9 xmax: 23 ymax: 46.2
# Geodetic CRS: WGS 84
# First 10 features:
# gml_id ID_Municip NameASCII NameLatin Area SHAPE_Leng
# 1 POP_age.1 70335 Bosilegrad Bosilegrad 571273097 121715
# 2 POP_age.2 80195 Kanjiza Kanji�a 398623963 94729
# 3 POP_age.3 80438 Subotica Subotica 100734608 164832
# 4 POP_age.4 70572 Kladovo Kladovo 627254771 137660
# 5 POP_age.5 80454 Titel Titel 260745278 104386
# 6 POP_age.6 80110 Becej Becej 486479140 130561
# 7 POP_age.7 80268 Novi Becej Novi Becej 608393938 157111
# 8 POP_age.8 80136 Zabalj �abalj 399798048 127101
# 9 POP_age.9 80390 Srbobran Srbobran 284106212 89115
# 10 POP_age.10 80152 Zrenjanin Zrenjanin 132585270 272176
# SHAPE_Area NUTS0 NUTS1 NUTS2 NUTS3 TOTAL_POP ADULTS AVARAGE
# 1 5.71e+08 RS RS2 RS22 RS228 8129 6843 45.1774511
# 2 3.98e+08 RS RS1 RS12 RS124 25343 20842 42.44057531
# 3 1.01e+09 RS RS1 RS12 RS125 141554 116545 41.90601467
# 4 6.27e+08 RS RS2 RS22 RS221 20635 17644 46.75699055
# 5 2.61e+08 RS RS1 RS12 RS123 15738 12747 41.21559283
# 6 4.86e+08 RS RS1 RS12 RS123 37351 30217 41.47866188
# 7 6.08e+08 RS RS1 RS12 RS126 23925 19566 41.50948798
# 8 4.00e+08 RS RS1 RS12 RS123 26134 20616 39.71022423
# 9 2.84e+08 RS RS1 RS12 RS123 16317 13189 41.12824049
# 10 1.33e+09 RS RS1 RS12 RS126 123362 101780 42.19447642
# the_geom
# 1 MULTIPOLYGON (((22.3 42.6, ...
# 2 MULTIPOLYGON (((19.9 46.2, ...
# 3 MULTIPOLYGON (((19.7 46.2, ...
# 4 MULTIPOLYGON (((22.5 44.7, ...
# 5 MULTIPOLYGON (((20.2 45.3, ...
# 6 MULTIPOLYGON (((20.1 45.7, ...
# 7 MULTIPOLYGON (((20.3 45.8, ...
# 8 MULTIPOLYGON (((20.1 45.5, ...
# 9 MULTIPOLYGON (((20.1 45.5, ...
# 10 MULTIPOLYGON (((20.4 45.6, ...
gk_srb = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
pop = st_transform(pop, gk_srb)
pop
# Simple feature collection with 197 features and 14 fields
# Geometry type: MULTIPOLYGON
# Dimension: XY
# Bounding box: xmin: 7330000 ymin: 4630000 xmax: 7660000 ymax: 5120000
# Projected CRS: +proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m
# First 10 features:
# gml_id ID_Municip NameASCII NameLatin Area SHAPE_Leng
# 1 POP_age.1 70335 Bosilegrad Bosilegrad 571273097 121715
# 2 POP_age.2 80195 Kanjiza Kanji�a 398623963 94729
# 3 POP_age.3 80438 Subotica Subotica 100734608 164832
# 4 POP_age.4 70572 Kladovo Kladovo 627254771 137660
# 5 POP_age.5 80454 Titel Titel 260745278 104386
# 6 POP_age.6 80110 Becej Becej 486479140 130561
# 7 POP_age.7 80268 Novi Becej Novi Becej 608393938 157111
# 8 POP_age.8 80136 Zabalj �abalj 399798048 127101
# 9 POP_age.9 80390 Srbobran Srbobran 284106212 89115
# 10 POP_age.10 80152 Zrenjanin Zrenjanin 132585270 272176
# SHAPE_Area NUTS0 NUTS1 NUTS2 NUTS3 TOTAL_POP ADULTS AVARAGE
# 1 5.71e+08 RS RS2 RS22 RS228 8129 6843 45.1774511
# 2 3.98e+08 RS RS1 RS12 RS124 25343 20842 42.44057531
# 3 1.01e+09 RS RS1 RS12 RS125 141554 116545 41.90601467
# 4 6.27e+08 RS RS2 RS22 RS221 20635 17644 46.75699055
# 5 2.61e+08 RS RS1 RS12 RS123 15738 12747 41.21559283
# 6 4.86e+08 RS RS1 RS12 RS123 37351 30217 41.47866188
# 7 6.08e+08 RS RS1 RS12 RS126 23925 19566 41.50948798
# 8 4.00e+08 RS RS1 RS12 RS123 26134 20616 39.71022423
# 9 2.84e+08 RS RS1 RS12 RS123 16317 13189 41.12824049
# 10 1.33e+09 RS RS1 RS12 RS126 123362 101780 42.19447642
# the_geom
# 1 MULTIPOLYGON (((7606345 471...
# 2 MULTIPOLYGON (((7418828 511...
# 3 MULTIPOLYGON (((7397721 511...
# 4 MULTIPOLYGON (((7617020 495...
# 5 MULTIPOLYGON (((7435090 502...
# 6 MULTIPOLYGON (((7427241 506...
# 7 MULTIPOLYGON (((7447076 507...
# 8 MULTIPOLYGON (((7429999 504...
# 9 MULTIPOLYGON (((7426516 504...
# 10 MULTIPOLYGON (((7452032 505...
# Karta opština u Merkatorovoj projekciji
plot(st_geometry(pop), graticule = TRUE, border = 'grey', axes = TRUE)
import geopandas as gpd
import matplotlib.pyplot as plt
import requests
# granice opština u Srb
url = 'http://osgl.grf.bg.ac.rs/geoserver/osgl_4/wfs' + \
'?service=WFS&version=1.0.0&request=GetFeature&typeName=osgl_4:POP_age'
response = requests.get(url)
# snimamo fajl na disk
open('data/pop.gml', 'wb').write(response.content)
# 9461553
gdf = gpd.read_file('data/pop.gml')
# Podaci su u WGS84 (EPSG:4326)
gdf.crs = 'epsg:4326'
gdf
# gml_id ... geometry
# 0 POP_age.1 ... MULTIPOLYGON (((22.29045 42.59307, 22.29047 42...
# 1 POP_age.2 ... MULTIPOLYGON (((19.94315 46.17601, 19.94470 46...
# 2 POP_age.3 ... MULTIPOLYGON (((19.66958 46.18402, 19.66976 46...
# 3 POP_age.4 ... MULTIPOLYGON (((22.47150 44.71333, 22.47564 44...
# 4 POP_age.5 ... MULTIPOLYGON (((20.16648 45.32598, 20.16532 45...
# .. ... ... ...
# 192 POP_age.193 ... MULTIPOLYGON (((21.28057 42.44932, 21.28637 42...
# 193 POP_age.194 ... MULTIPOLYGON (((21.56451 42.73154, 21.56464 42...
# 194 POP_age.195 ... MULTIPOLYGON (((21.46112 42.62940, 21.46216 42...
# 195 POP_age.196 ... MULTIPOLYGON (((20.59400 42.88168, 20.60346 42...
# 196 POP_age.197 ... MULTIPOLYGON (((19.54257 44.48493, 19.54272 44...
#
# [197 rows x 15 columns]
# transformišemo u GK DKS projekciju
gk_srb = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
gdf = gdf.to_crs(gk_srb)
gdf
# gml_id ... geometry
# 0 POP_age.1 ... MULTIPOLYGON (((7606345.057 4717346.371, 76063...
# 1 POP_age.2 ... MULTIPOLYGON (((7418828.312 5115172.800, 74189...
# 2 POP_age.3 ... MULTIPOLYGON (((7397721.229 5116379.823, 73977...
# 3 POP_age.4 ... MULTIPOLYGON (((7617020.475 4953142.328, 76173...
# 4 POP_age.5 ... MULTIPOLYGON (((7435089.985 5020499.619, 74349...
# .. ... ... ...
# 192 POP_age.193 ... MULTIPOLYGON (((7523517.913 4700608.490, 75239...
# 193 POP_age.194 ... MULTIPOLYGON (((7546664.236 4732072.125, 75466...
# 194 POP_age.195 ... MULTIPOLYGON (((7538260.358 4720675.646, 75383...
# 195 POP_age.196 ... MULTIPOLYGON (((7467272.479 4748673.511, 74680...
# 196 POP_age.197 ... MULTIPOLYGON (((7384505.118 4927736.755, 73845...
#
# [197 rows x 15 columns]
# Karta
ax = gdf.plot(edgecolor='grey', figsize=(10, 8))
ax.set_axis_on()
ax.set_xlabel('E')
ax.set_ylabel('N')
plt.grid(True)
plt.show()
Primer 5: Inverzni zadatak Gaus-Krigerova projekcija
Sračunati elipsoidne koordinate za tačke T1(7523517.93, 4700608.49) i T2(7384505.11, 4927736.75) zadate u Gaus-Krigerovoj projekciji. Koordinate prikazati i u obliku stepen, minut i sekund.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Za tacke sa koordinatama T1(7523517.93, 4700608.49) i T2(7384505.11, 4927736.75)
# u GK DKS projekciji
gk_srb = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
# tačke u projekciji
tgk= st_sfc( st_point(c(7523517.93, 4700608.49)), st_point(c(7384505.11, 4927736.75)),
crs = gk_srb )
# inverzni zadatak iz pravouglih u longitudu, latitudu
bes_crs = "+proj=longlat +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89"
tLL = st_transform(tgk,
crs = bes_crs)
ll = st_coordinates(tLL)
# Koordinate treba zaokružiti do na cm ili dm, što je oko 6. decimale
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
round(ll,6)
# X Y
# [1,] 21.285940 42.449019
# [2,] 19.547831 44.484896
# gedetska dužina i širina
# lon lat
lon = ll[,1]
lat = ll[,2]
# funkcija za stepen u stepen minut sekund
deg2dms <- function(deg){
deg_sign = sign(deg)
deg = abs(deg)
DEG = floor(deg)
MIN = floor((deg - DEG) * 60)
SEC = (deg - DEG - MIN/60) * 3600
SEC=round(SEC,2)
dms=paste(deg_sign*DEG,'\u00B0',MIN,"'",SEC,"''",sep='')
return(dms)
}
# gedetska dužina i širina
print(paste("T1 " ,deg2dms(lon[1]), deg2dms(lat[1])) )
# [1] "T1 21°17'9.39'' 42°26'56.47''"
print(paste( "T2 " ,deg2dms(lon[2]), deg2dms(lat[2])) )
# [1] "T2 19°32'52.19'' 44°29'5.63''"import shapely.geometry
import geopandas as gpd
# pravimo GeoDataFrame koordinate u LCC projekciji
data = {'geometry': [shapely.geometry.Point(7523517.93, 4700608.49), shapely.geometry.Point(7384505.11, 4927736.75)]}
gk_srb = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
gdf = gpd.GeoDataFrame(data, crs=gk_srb) # gk_srb
# transformacija na bes_crs
bes_crs = "+proj=longlat +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89"
gdf_bes = gdf.to_crs(bes_crs)
print(gdf_bes)
# geometry
# 0 POINT (21.28594 42.44902)
# 1 POINT (19.54783 44.48490)
# Prikaz koordinata na 6 decimala
# (0.000001 * pi/180 )* 6377000 m = 0.11 m
lon = gdf_bes["geometry"].x
lat = gdf_bes["geometry"].y
# gedetska dužina i širina
print("T1 " ,round(lon[0],6), round(lat[0],6))
# T1 21.28594 42.449019
print("T2 " ,round(lon[1],6), round(lat[1],6))
# T2 19.547831 44.484896
# funkcija za stepen u stepen minut sekund
def deg2dms(deg):
deg_sign = 1 if deg >= 0 else -1
deg = abs(deg)
DEG = int(deg)
MIN = int((deg - DEG) * 60)
SEC = (deg - DEG - MIN / 60) * 3600
SEC = round(SEC, 2)
dms = f"{deg_sign * DEG}\u00B0{MIN}'{SEC}''"
return dms
# gedetska dužina i širina
print(f"T1 {deg2dms(lon[0])} {deg2dms(lat[0])}")
# T1 21°17'9.39'' 42°26'56.47''
print(f"T2 {deg2dms(lon[1])} {deg2dms(lat[1])}")
# T2 19°32'52.19'' 44°29'5.63''Primer 6: Koordinate iste tačke u 6. i 7. zoni
Za tačku u Somboru sa koordinatama \(\lambda=19.108343\) i \(\varphi=45.767426\) sračunati pravougle koordinate i u 6. i 7. zoni.
library(sf)
# globalna opcija za broj cifara koji se ispisuju u konzoli
options(digits = 12)
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
so = st_point( c(19.108343, 45.767426) ) # lon , lat
# potom pravimo kolekciju geometrije sfc u odgovarajućoj projekciji
bes_crs = "+proj=longlat +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89"
pts_sfc = st_sfc(so, crs=bes_crs)
# GK Srb koord. ref. sis.
gk_srb6 = "+proj=tmerc +lat_0=0 +lon_0=18 +k=0.9999 +x_0=6500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
gk_srb7 = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
# transformacija u GK
pts_sfc_gk6 = st_transform(pts_sfc, crs =gk_srb6)
# pts_sfc_gk6
# matrica koordinata iz prostornih podataka zona 6
# st_coordinates(pts_sfc_gk6)
# koordinate treba zaokružiti do na cm
round(st_coordinates(pts_sfc_gk6),2)
# X Y
# [1,] 6586195.71 5069811.38
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
# transformacija u GK
pts_sfc_gk7 = st_transform(pts_sfc, crs =gk_srb7)
# pts_sfc_gk7
# matrica koordinata iz prostornih podataka zona 7
# st_coordinates(pts_sfc_gk7)
# koordinate treba zaokružiti do na cm
round(st_coordinates(pts_sfc_gk7),2)
# X Y
# [1,] 7352886.5 5070954.37
# NAPOMENA u R sf paketu koordinate imaju oznaku X,Y kao u matematici
# REDOSLED KOORDINATA JE E,N (pravac istoka, pravac severa)
import shapely.geometry
import geopandas as gpd
# Kreirati prostorni lejer sa pozicijom zgrade Građevinskog fakulteta
# prvi nivo je je sfg objekat koji je samo geometrijski primitiv
so = shapely.geometry.Point(19.108343, 45.767426)
# potom pravimo kolekciju geometrije sa koor. ref.sis
bes_crs = "+proj=longlat +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89"
so_geom_proj = gpd.GeoSeries([so], crs=bes_crs)
# prostorni lejer
so_layer_proj = gpd.GeoDataFrame({'geometry': so_geom_proj})
# GK Srb koord. ref. sis.
gk_srb6 = "+proj=tmerc +lat_0=0 +lon_0=18 +k=0.9999 +x_0=6500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
gk_srb7 = "+proj=tmerc +lat_0=0 +lon_0=21 +k=0.9999 +x_0=7500000 +y_0=0 +ellps=bessel +towgs84=574.027,170.175,401.545,4.88786,-0.66524,-13.24673,6.89 +units=m"
# transformacija u GK projekciju
print(so_layer_proj.to_crs(gk_srb6))
# geometry
# 0 POINT (6586195.708 5069811.378)
print(so_layer_proj.to_crs(gk_srb7))
# geometry
# 0 POINT (7352886.498 5070954.372)